吉林省松原市前郭县名校调研系列(省命题A)2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-05-25 类型:期中考试
一、单选题
-
1. 9的算术平方根是( )A、 B、 C、 D、2. 在平面直角坐标系中,下列各点位于第三象限的是( )A、 B、 C、 D、3. 如图,已知直线 、 被直线 所截, ,若 ,则 等于( )
 A、 B、 C、 D、4. 在下列各数中,是无理数的是( )A、0.12 B、 C、 D、5. 如图是一所学校的部分平面示意图,在同一平面直角坐标系中,若体育馆A的坐标为 ,科技馆B的坐标为 ,则教学楼C的坐标为( )
A、 B、 C、 D、4. 在下列各数中,是无理数的是( )A、0.12 B、 C、 D、5. 如图是一所学校的部分平面示意图,在同一平面直角坐标系中,若体育馆A的坐标为 ,科技馆B的坐标为 ,则教学楼C的坐标为( ) A、 B、 C、 D、6. 如图,下列条件中能判定 的是( )
A、 B、 C、 D、6. 如图,下列条件中能判定 的是( )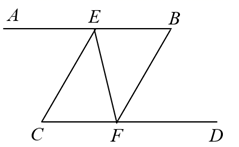 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
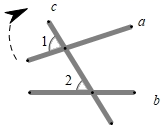
7. 的立方根是 .8. 如图,将木条a , b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是 .
 9. 在平面直角坐标系中,将点 向左平移 个单位长度,则平移后对应的点 的坐标是 .10. 如图,在数轴上,点B与点A到原点的距离相等,则点B表示的实数是。
9. 在平面直角坐标系中,将点 向左平移 个单位长度,则平移后对应的点 的坐标是 .10. 如图,在数轴上,点B与点A到原点的距离相等,则点B表示的实数是。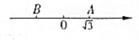 11. 下列命题中,①对顶角相等;②同位角相等;③平行于同一条直线的两条直线平行;④若 ,则 .是真命题的是 . (填序号)12. 若一个正数的两个不同的平方根分别是5和3m+1,则m=13. 如图,在平面直角坐标系中,AB平行于x轴,点A的坐标为(4,3),点B在点A的左侧,AB=a,若点B在第二象限,则a的取值范围是
11. 下列命题中,①对顶角相等;②同位角相等;③平行于同一条直线的两条直线平行;④若 ,则 .是真命题的是 . (填序号)12. 若一个正数的两个不同的平方根分别是5和3m+1,则m=13. 如图,在平面直角坐标系中,AB平行于x轴,点A的坐标为(4,3),点B在点A的左侧,AB=a,若点B在第二象限,则a的取值范围是 14. 如图,已知AD∥BE,点C是直线FG上的动点,若在点C的移动过程中,存在某时刻使得∠ACB=45°, ∠DAC=22°,则∠EBC的度数为.
14. 如图,已知AD∥BE,点C是直线FG上的动点,若在点C的移动过程中,存在某时刻使得∠ACB=45°, ∠DAC=22°,则∠EBC的度数为.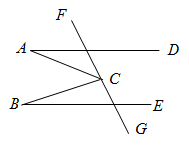
三、解答题
-
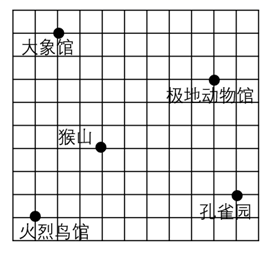
15. 计算: .16. 如图,图中每个小正方形的边长均为1,已知极地动物馆的坐标为 ,孔雀园的坐标为 ,先建立平面直角坐标系,再表示其他三个景点的坐标.
 17. 如图,直线AB、CD相交于点O,过点O作OE⊥AB,OF平分∠BOD.
17. 如图,直线AB、CD相交于点O,过点O作OE⊥AB,OF平分∠BOD.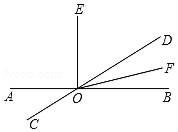 (1)、直接写出∠AOC的补角;(2)、若∠AOC=40°,求∠EOF的度数.18. 求下列各式中x的值.(1)、 ;(2)、 .19. 已知 的算术平方根是1, 的立方根是2.(1)、求x、y的值;(2)、求 的平方根.20. 如图,已知 , ,试猜想 与 之间有怎样的位置关系?并说明理由.请你将下列证明过程补充完整.
(1)、直接写出∠AOC的补角;(2)、若∠AOC=40°,求∠EOF的度数.18. 求下列各式中x的值.(1)、 ;(2)、 .19. 已知 的算术平方根是1, 的立方根是2.(1)、求x、y的值;(2)、求 的平方根.20. 如图,已知 , ,试猜想 与 之间有怎样的位置关系?并说明理由.请你将下列证明过程补充完整.
结论: .
证明: (已知),
▲ ( ▲ ),
▲ ▲ (两直线平行,同位角相等).
又 (已知),
▲ ▲ (等量代换),
( ▲ ).
21. 小明想用一块面积为400平方厘米的正方形纸片,沿着边的方向,裁出一块面积为360平方厘米的长方形纸片,使它的长宽之比为4:3,他不知道能否裁得出来,聪明的你帮他想想,他能裁得出来吗?(通过计算说明)22. 如图,在平面直角坐标系中,已知点 、 、 , 是三角形 的边 上的任意一点,三角形 经过平移后得到三角形 ,点P的对应点为 .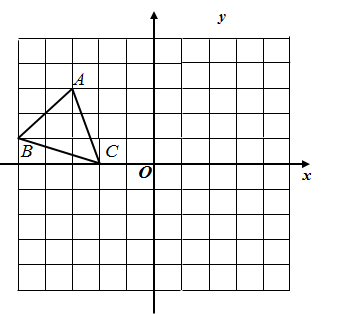 (1)、直接写出点 、 、 的坐标(点A、B、C的对应点分别为 、 、 );(2)、在图中画出三角形 .23. 如图,已知AB//CD,AC平分 ,且 , .
(1)、直接写出点 、 、 的坐标(点A、B、C的对应点分别为 、 、 );(2)、在图中画出三角形 .23. 如图,已知AB//CD,AC平分 ,且 , .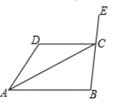 (1)、求 的度数;(2)、求 的度数.24. 在平面直角坐标系中,已知点 .(1)、若点M在y轴上,求a的值;(2)、若点M到x轴的距离为 ,求点M的坐标;(3)、若点M在过点 且与y轴平行的直线上,求点M的坐标.
(1)、求 的度数;(2)、求 的度数.24. 在平面直角坐标系中,已知点 .(1)、若点M在y轴上,求a的值;(2)、若点M到x轴的距离为 ,求点M的坐标;(3)、若点M在过点 且与y轴平行的直线上,求点M的坐标.
