山西省孝义市2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-05-25 类型:期中考试
一、单选题
-
1. 下列是四个汽车标志图案,其中可看作由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 的平方根为( )A、 B、 C、 D、3. 下列四个命题:①两条直线相交,若对顶角互补,则这两条直线互相垂直;②两条直线被第三条直线所截,内错角相等;③如果两条直线都与第三条直线平行,那么这两条直线也互相平行;④经过直线外一点,有且只有一条直线与已知直线平行.其中是真命题的个数是( )A、1 B、2 C、3 D、44. 在平面直角坐标系中,将点 向右平移 个单位长度后得到点的坐标为 ,则 的值为( )A、1 B、3 C、5 D、145. 与数 最接近的整数是( )A、4 B、5 C、6 D、76. 如图, ,将一个含 角的直角三角尺按如图所示的方式放置,若 的度数为 ,则 的度数为( )
2. 的平方根为( )A、 B、 C、 D、3. 下列四个命题:①两条直线相交,若对顶角互补,则这两条直线互相垂直;②两条直线被第三条直线所截,内错角相等;③如果两条直线都与第三条直线平行,那么这两条直线也互相平行;④经过直线外一点,有且只有一条直线与已知直线平行.其中是真命题的个数是( )A、1 B、2 C、3 D、44. 在平面直角坐标系中,将点 向右平移 个单位长度后得到点的坐标为 ,则 的值为( )A、1 B、3 C、5 D、145. 与数 最接近的整数是( )A、4 B、5 C、6 D、76. 如图, ,将一个含 角的直角三角尺按如图所示的方式放置,若 的度数为 ,则 的度数为( )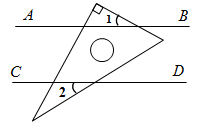 A、 B、 C、 D、7. 如图,已知 , 平分 ,若 ,则 的度数为( ).
A、 B、 C、 D、7. 如图,已知 , 平分 ,若 ,则 的度数为( ). A、 B、 C、 D、8. 五子棋深受广大小朋友的喜爱,规则如下:在正方形棋盘中,由黑方先行,轮流摆子,在任意方向(横向、竖向或斜向)上先连成五枚棋子者获胜,如图是小明和小亮的部分对弈图,若棋子 的坐标为 , 的坐标为 ,则点 的坐标为( )
A、 B、 C、 D、8. 五子棋深受广大小朋友的喜爱,规则如下:在正方形棋盘中,由黑方先行,轮流摆子,在任意方向(横向、竖向或斜向)上先连成五枚棋子者获胜,如图是小明和小亮的部分对弈图,若棋子 的坐标为 , 的坐标为 ,则点 的坐标为( ) A、 B、 C、 D、9. 下列各数:① 、②-0.1010010001、③ 、④ 、⑤ 、⑥ 中,其中无理数有( )A、2个 B、3个 C、4个 D、5个10. 折纸是我国的传统文化,折纸不仅和自然科学结合在一起,还发展出了折纸几何学,成为现代几何学的一个分支,折纸过程中既要动脑又要动手.如图,将一长方形纸条首先沿着 进行第一次折叠,使得 , 两点落在 、 的位置,再将纸条沿着 折叠( 与 在同一直线上),使得 、 分别落在 、 的位置.若 ,则 的度数为( )
A、 B、 C、 D、9. 下列各数:① 、②-0.1010010001、③ 、④ 、⑤ 、⑥ 中,其中无理数有( )A、2个 B、3个 C、4个 D、5个10. 折纸是我国的传统文化,折纸不仅和自然科学结合在一起,还发展出了折纸几何学,成为现代几何学的一个分支,折纸过程中既要动脑又要动手.如图,将一长方形纸条首先沿着 进行第一次折叠,使得 , 两点落在 、 的位置,再将纸条沿着 折叠( 与 在同一直线上),使得 、 分别落在 、 的位置.若 ,则 的度数为( )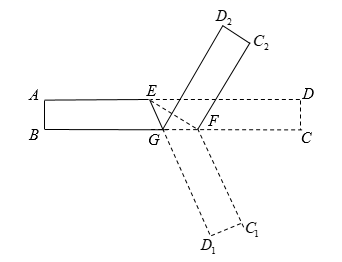 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
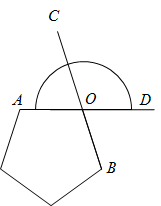
11. 如图是某城市一座古塔底部平面图,在不能进入塔内测量的情况下,学习兴趣小组设计了如图所示的一种测量方案,学习兴趣小组认为测得 的度数就是 的度数.其中的数学原理是 .
 12. 若 , ,那么 .13. 如图,将面积为5的正方形放在数轴上,以表示-1的点为圆心,以正方形的边长为半径作圆,交数轴于点 , 两点,则点 , 表示的数分别为 .
12. 若 , ,那么 .13. 如图,将面积为5的正方形放在数轴上,以表示-1的点为圆心,以正方形的边长为半径作圆,交数轴于点 , 两点,则点 , 表示的数分别为 .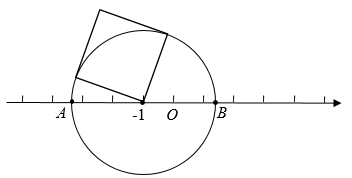 14. 点 是第四象限内一点,若点 到两坐标轴的距离相等,则点 的坐标为 .15. 如图,将直角三角形 沿着 方向平移得到三角形 ,若 , , ,图中阴影部分的面积为 ,则三角形 沿着 方向平移的距离为 .
14. 点 是第四象限内一点,若点 到两坐标轴的距离相等,则点 的坐标为 .15. 如图,将直角三角形 沿着 方向平移得到三角形 ,若 , , ,图中阴影部分的面积为 ,则三角形 沿着 方向平移的距离为 .
三、解答题
-
16. 计算:(1)、(2)、17. 已知 ,求 的值.18. 如图,点 , , 分别是三角形 的边 , , 上的点, , .求证: .
 19. 如图,在平面直角坐标系中,三角形 的顶点都在格点上,每个小正方形的边长为1.
19. 如图,在平面直角坐标系中,三角形 的顶点都在格点上,每个小正方形的边长为1. (1)、请直接写出 、 、 各点的坐标;
(1)、请直接写出 、 、 各点的坐标;( , )、 ( , )、 ( , );
(2)、将三角形 向上平移2个单位,得到三角形 .①请在图中画出三角形 .
②直接写出三角形 扫过的区域的面积.
20. 通过《实数》一章的学习,我们知道 是一个无限不循环小数,因此 的小数部分我们不可能全部写出来.聪明的小丽认为 的整数部分为1,所以 减去其整数部分,差就是 的小数部分,所以用 来表示 的小数部分.根据小丽的方法请完成下列问题:(1)、 的整数部分为 , 小数部分为 .(2)、已知 的整数部分 , 的整数部分为 ,求 的立方根.21. 阅读与思考,阅读下列材料,并完成相应的任务.三角形的内角和
小学时候我们就知道三角形内角和是 ,学习了平行线之后,可以证明三角形内角和是 ,证明方法如下:
如图1,已知:三角形 .求证: .
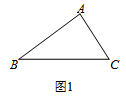
方法一:如图2,过点 作 于点 ,过点 作 ,过点 作 .
∵ , , ,
∴ , , ,
∴ ,
∴ ,(依据一)
∴ ,
又∵ ,
∴ ,
∴ (依据二)
∴

方法二:如图3,在边 上任取一点 (不与 , 重合),连接 .分别过点 , 作 的平行线……
 (1)、任务一:材料中方法一的证明过程中的依据一,依据二分别指的是:
(1)、任务一:材料中方法一的证明过程中的依据一,依据二分别指的是:依据一: ;
依据二: .
(2)、任务二:材料中证法一的思路是用平行线的性质得到 , ,将三角形内角和问题转化为 与 的和,再通过平行线的性质得到 ,进而得到三角形内角和是 ,这种方法主要体现的数学思想是__________(将正确选项代码填入空格处).A、数形结合思想 B、分类思想 C、转化思想(3)、任务三:请将方法二的证明过程补充完整,在图3中作出辅助线,并标清字母.22. 综合与探究.如图1,在平面直角坐标系中,点 , 的坐标分别为 , ,将线段 沿 轴方向向右平移,得到线段 ,点 的对应点 的坐标为 ,连接 .点 是 轴上一动点. (1)、请你直接写出点 的坐标 .(2)、如图1,当点 在线段 上时(不与点 、 重合),分别连接 , .猜想 , , 之间的数量关系,并说明理由.(3)、①如图2,当点 在点 上方时,猜想 , , 之间的数量关系,并说明理由.
(1)、请你直接写出点 的坐标 .(2)、如图1,当点 在线段 上时(不与点 、 重合),分别连接 , .猜想 , , 之间的数量关系,并说明理由.(3)、①如图2,当点 在点 上方时,猜想 , , 之间的数量关系,并说明理由.②如图3,当点 在 轴的负半轴上时,请你直接写出 , , 之间的数量关系.