北京市大兴区2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-05-25 类型:期中考试
一、单选题
-
1. 下面 与 不是对顶角的是( )A、
 B、
B、 C、
C、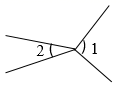 D、
D、 2. 16的算术平方根是( )A、2 B、±2 C、4 D、±43. 下面的每组图形中,平移左边图形可以得到右边图形的一组是( )A、
2. 16的算术平方根是( )A、2 B、±2 C、4 D、±43. 下面的每组图形中,平移左边图形可以得到右边图形的一组是( )A、 B、
B、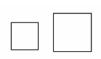 C、
C、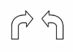 D、
D、 4. 下列图形中,∠1与∠2是同旁内角的是( )A、
4. 下列图形中,∠1与∠2是同旁内角的是( )A、 B、
B、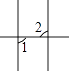 C、
C、 D、
D、 5. 下列等式正确的是( )A、 B、 C、 D、6. 下列命题:①直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;②过一点有且只有一条直线与这条直线平行;③垂线段最短;④同旁内角互补.其中,真命题有( )A、3个 B、2个 C、1个 D、0个7. 在平面直角坐标系中,在第二象限内有一点P , 它到x轴的距离为4,到y轴的距离为5,则点P的坐标为( )A、(﹣5,4) B、(﹣4,5) C、(4,5) D、(5,﹣4)8. 如图,数轴上有 , , , 四点,则这四个点所表示的数与 最接近的是( )
5. 下列等式正确的是( )A、 B、 C、 D、6. 下列命题:①直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;②过一点有且只有一条直线与这条直线平行;③垂线段最短;④同旁内角互补.其中,真命题有( )A、3个 B、2个 C、1个 D、0个7. 在平面直角坐标系中,在第二象限内有一点P , 它到x轴的距离为4,到y轴的距离为5,则点P的坐标为( )A、(﹣5,4) B、(﹣4,5) C、(4,5) D、(5,﹣4)8. 如图,数轴上有 , , , 四点,则这四个点所表示的数与 最接近的是( ) A、点 B、点 C、点 D、点
A、点 B、点 C、点 D、点二、填空题
-
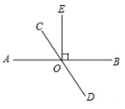
9. 2的平方根是 .10. 实数 ,0, ,3.14159, , ,0.010010001……(相邻两个1之间依次多一个0),其中,无理数有个.11. 如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC=°.
 12. 如图,要把池中的水引到 处,且使所开渠道最短,可过 点作 于 ,然后沿所作的线段 开渠,所开渠道即最短,试说明设计的依据是: .
12. 如图,要把池中的水引到 处,且使所开渠道最短,可过 点作 于 ,然后沿所作的线段 开渠,所开渠道即最短,试说明设计的依据是: . 13. 若点P(2﹣m,3m+1)在坐标轴上,则点P的坐标为 .14. 若 ,则 .15. 如图,把图①中的长方形分成 、 两部分,恰与正方形 拼接成如图②的大正方形.如果正方形A的面积为2,拼接后的大正方形的面积是5,则图①中原长方形的长和宽分别是 .
13. 若点P(2﹣m,3m+1)在坐标轴上,则点P的坐标为 .14. 若 ,则 .15. 如图,把图①中的长方形分成 、 两部分,恰与正方形 拼接成如图②的大正方形.如果正方形A的面积为2,拼接后的大正方形的面积是5,则图①中原长方形的长和宽分别是 . 16. 如图,在平面直角坐标系下 中,我们把横、纵坐标都是整数的点叫做整点.已知点 ,点 是 轴正半轴上的整点,记 内部(不包括边界)的整点个数为 .当点 的横坐标为3时, ;当点 的横坐标为 ( 为正整数)时, . (用含 的代数式表示)
16. 如图,在平面直角坐标系下 中,我们把横、纵坐标都是整数的点叫做整点.已知点 ,点 是 轴正半轴上的整点,记 内部(不包括边界)的整点个数为 .当点 的横坐标为3时, ;当点 的横坐标为 ( 为正整数)时, . (用含 的代数式表示)
三、解答题
-
17. 计算: .18. 计算: .19. 计算: .20. 已知(x-1)2 =4,求x的值.21. 如图,点A在 的一边上,按要求画图并填空.
 (1)、过点 画直线 于点 ,与 的另一边相交于点 .(2)、过点 画 的垂线段 ,垂足为点 .(3)、过点 画直线 ,交直线 于点 .(4)、 .(5)、如果 , , ,则点A到直线 的距离为 .22. 如图,图中的小方格都是边长为1的正方形, 的顶点坐标为 , , .
(1)、过点 画直线 于点 ,与 的另一边相交于点 .(2)、过点 画 的垂线段 ,垂足为点 .(3)、过点 画直线 ,交直线 于点 .(4)、 .(5)、如果 , , ,则点A到直线 的距离为 .22. 如图,图中的小方格都是边长为1的正方形, 的顶点坐标为 , , . (1)、请在图中画出 向左平移5个单位长度的图形 ;(2)、写出点 , , 的坐标.23. 如图,是小明所在学校的平面示意图,已知宿舍楼的位置是(3,4),艺术楼的位置是(﹣3,1).
(1)、请在图中画出 向左平移5个单位长度的图形 ;(2)、写出点 , , 的坐标.23. 如图,是小明所在学校的平面示意图,已知宿舍楼的位置是(3,4),艺术楼的位置是(﹣3,1). (1)、根据题意,画出相应的平面直角坐标系;(2)、分别写出教学楼、体育馆的位置;(3)、若学校行政楼的位置是(﹣1,﹣1),在图中标出行政楼的位置.24. 完成下面的证明,如图, , ,求证: .
(1)、根据题意,画出相应的平面直角坐标系;(2)、分别写出教学楼、体育馆的位置;(3)、若学校行政楼的位置是(﹣1,﹣1),在图中标出行政楼的位置.24. 完成下面的证明,如图, , ,求证: .证明:∵ (已知),
∴ ▲ ( ▲ )
∵ (已知),
∴ ▲ ( ▲ ).
∴ ▲ ( ▲ ).
∴ (等量代换).
 25. 如图,点 在直线 上, , 与 互余, 是 上一点,连接 OE.
25. 如图,点 在直线 上, , 与 互余, 是 上一点,连接 OE. (1)、求证: .(2)、若 平分 , ,求 的度数.26. 在平面直角坐标系 中描出下列两组点,分别将每组里的点用线段依次连接起来.
(1)、求证: .(2)、若 平分 , ,求 的度数.26. 在平面直角坐标系 中描出下列两组点,分别将每组里的点用线段依次连接起来.第一组: 、 ;
第二组: 、 .
 (1)、直接写出线段 与线段 的位置关系;(2)、在(1)的条件下,线段 , 分别与 轴交于点 , .若点 为射线 上一动点(不与点 , 重合).
(1)、直接写出线段 与线段 的位置关系;(2)、在(1)的条件下,线段 , 分别与 轴交于点 , .若点 为射线 上一动点(不与点 , 重合).①当点 在线段 上运动时,连接 、 ,补全图形,用等式表示 、 、 之间的数量关系,并证明.
②当 与 面积相等时,求点 的坐标.

