北京市海淀区2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-05-25 类型:期中考试
一、单选题
-
1. 9的算术平方根是( )A、 81 B、3 C、±3 D、-32. 在平面直角坐标系中,点M(2,3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列实数 , , (相邻两个1之间依次多一个0), , , 中,无理数有( )A、1个 B、2个 C、3个 D、4个4. 如图,直线 被c所截,则 和 是( )
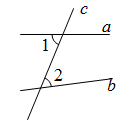 A、同位角 B、内错角 C、同旁内角 D、邻补角5. 下列各数中一定有平方根的是( )A、 B、 C、 D、6. 一把直尺和一个含 , 角的三角板如图所示摆放,直尺一边与三角板的两直角边分别交于F,A两点,另一边与三角板的两直角边分别交于D,E两点,且 ,那么 的大小为( )
A、同位角 B、内错角 C、同旁内角 D、邻补角5. 下列各数中一定有平方根的是( )A、 B、 C、 D、6. 一把直尺和一个含 , 角的三角板如图所示摆放,直尺一边与三角板的两直角边分别交于F,A两点,另一边与三角板的两直角边分别交于D,E两点,且 ,那么 的大小为( ) A、 B、 C、 D、7. 如图,直线AB , CD相交于点O , 分别作∠AOD , ∠BOD的平分线OE , OF . 将直线CD绕点O旋转,下列数据与∠BOD大小变化无关的是( )
A、 B、 C、 D、7. 如图,直线AB , CD相交于点O , 分别作∠AOD , ∠BOD的平分线OE , OF . 将直线CD绕点O旋转,下列数据与∠BOD大小变化无关的是( ) A、∠AOD的度数 B、∠AOC的度数 C、∠EOF的度数 D、∠DOF的度数8. 如示意图,小宇利用两个面积为1 dm2的正方形拼成了一个面积为2 dm2的大正方形,并通过测量大正方形的边长感受了 dm的大小. 为了感知更多无理数的大小,小宇利用类似拼正方形的方法进行了很多尝试,下列做法不能实现的是( )
A、∠AOD的度数 B、∠AOC的度数 C、∠EOF的度数 D、∠DOF的度数8. 如示意图,小宇利用两个面积为1 dm2的正方形拼成了一个面积为2 dm2的大正方形,并通过测量大正方形的边长感受了 dm的大小. 为了感知更多无理数的大小,小宇利用类似拼正方形的方法进行了很多尝试,下列做法不能实现的是( ) A、利用两个边长为2dm的正方形感知 dm的大小 B、利用四个直角边为3dm的等腰直角三角形感知 dm的大小 C、利用一个边长为 dm的正方形以及一个直角边为2dm的等腰直角三角形感知 dm的大小 D、利用四个直角边分别为1 dm和3 dm的直角三角形以及一个边长为2 dm的正方形感知 dm的大小
A、利用两个边长为2dm的正方形感知 dm的大小 B、利用四个直角边为3dm的等腰直角三角形感知 dm的大小 C、利用一个边长为 dm的正方形以及一个直角边为2dm的等腰直角三角形感知 dm的大小 D、利用四个直角边分别为1 dm和3 dm的直角三角形以及一个边长为2 dm的正方形感知 dm的大小二、填空题
-
9. 如图,要在河岸l上建一个水泵房D,修建引水渠到村庄C处.施工人员的做法是:过点C作 于点D,将水泵房建在了D处.这样修建引水渠 最短,既省人力又省物力,这样做蕴含的数学原理是 .
 10. 如图,两直线交于点O,若∠1+∠2=76°,则∠1=度.
10. 如图,两直线交于点O,若∠1+∠2=76°,则∠1=度.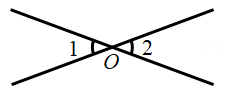 11. 如图,在四边形 中,点E在 的延长线上,连接 ,如果添加一个条件,使 ,那么可添加的条件为(写出一个即可).
11. 如图,在四边形 中,点E在 的延长线上,连接 ,如果添加一个条件,使 ,那么可添加的条件为(写出一个即可).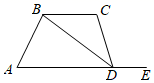 12. 在平面直角坐标系中,A点的坐标为( , ),若线段 ∥x轴,且 ,则点B的坐标为 .13. 用一个实数a的值说明命题“ ”是假命题,这个a的值可以是 .14. 为纪念戍边英雄,某班设计了《致敬英雄》主题宣传板报,黑板是一块长为2a米,宽为a米的长方形 ,版面设计如图所示,将它分割成两块边长均为a米的正方形 和正方形 ,分别以点 为圆心,正方形边长为半径画弧.阴影部分用图画展示英雄形象,空白部分用文字宣传英雄事迹.阴影部分的面积为平方米(用含a的代数式表示).
12. 在平面直角坐标系中,A点的坐标为( , ),若线段 ∥x轴,且 ,则点B的坐标为 .13. 用一个实数a的值说明命题“ ”是假命题,这个a的值可以是 .14. 为纪念戍边英雄,某班设计了《致敬英雄》主题宣传板报,黑板是一块长为2a米,宽为a米的长方形 ,版面设计如图所示,将它分割成两块边长均为a米的正方形 和正方形 ,分别以点 为圆心,正方形边长为半径画弧.阴影部分用图画展示英雄形象,空白部分用文字宣传英雄事迹.阴影部分的面积为平方米(用含a的代数式表示). 15. 为迎接校庆,某学校在东西走向的勤学路上修建了一排边长为1m的小正方形花坛,如图1所示. 小欢和小乐来到花坛边欣赏风景,小欢以自己所在的A点为原点,以向东的方向为正方向,以花坛对角线的长度 m为单位长度建立数轴,如图2所示. 若小乐在小欢的东15 m处,那么在图2的数轴上,小乐所在的点位于两个相邻整数之间,这两个整数分别是 .
15. 为迎接校庆,某学校在东西走向的勤学路上修建了一排边长为1m的小正方形花坛,如图1所示. 小欢和小乐来到花坛边欣赏风景,小欢以自己所在的A点为原点,以向东的方向为正方向,以花坛对角线的长度 m为单位长度建立数轴,如图2所示. 若小乐在小欢的东15 m处,那么在图2的数轴上,小乐所在的点位于两个相邻整数之间,这两个整数分别是 . 16. 在平面直角坐标系中,我们定义,点P沿着水平或竖直方向运动到达点Q的最短路径的长度为P , Q两点之间的“横纵距离”. 如图所示,点A的坐标为(2,3),则A , O两点之间的“横纵距离”为5
16. 在平面直角坐标系中,我们定义,点P沿着水平或竖直方向运动到达点Q的最短路径的长度为P , Q两点之间的“横纵距离”. 如图所示,点A的坐标为(2,3),则A , O两点之间的“横纵距离”为5 (1)、若点B的坐标为( ),则A , B两点之间的“横纵距离”为;(2)、已知点C的坐标为(0,2),D , O两点之间的“横纵距离”为5,D , C两点之间的“横纵距离”为3,请写出两个满足条件的点D的坐标: , .
(1)、若点B的坐标为( ),则A , B两点之间的“横纵距离”为;(2)、已知点C的坐标为(0,2),D , O两点之间的“横纵距离”为5,D , C两点之间的“横纵距离”为3,请写出两个满足条件的点D的坐标: , .三、解答题
-
17. 计算: .18. 完成下面的证明:已知:如图, .求证: ∥ .
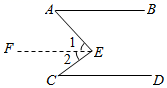
证明:过点 作 ∥ .
▲ ( ).
,
.
▲ ∥ ▲ ( ).
∥ ( ).
19. 计算: .20. 求出下列等式中x的值:(1)、 ;(2)、 .21. 已知:如图,直线 , 相交于点O, , 平分 ,求 的度数. 22. 如图,在平面直角坐标系中,三角形 的三个顶点分别是 , , .将三角形 先向右平移4个单位,再向下平移3个单位,得到三角形 .
22. 如图,在平面直角坐标系中,三角形 的三个顶点分别是 , , .将三角形 先向右平移4个单位,再向下平移3个单位,得到三角形 . (1)、请在图中画出平移后的三角形 ;(2)、三角形 的面积是 .23. 已知:实数a,b满足 .(1)、可得 , ;(2)、当一个正实数x的两个平方根分别为 和 时,求x的值.24. 已知:如图, ∥ , 和 交于点O,E为 上一点,F为 上一点,且 .求证: .
(1)、请在图中画出平移后的三角形 ;(2)、三角形 的面积是 .23. 已知:实数a,b满足 .(1)、可得 , ;(2)、当一个正实数x的两个平方根分别为 和 时,求x的值.24. 已知:如图, ∥ , 和 交于点O,E为 上一点,F为 上一点,且 .求证: .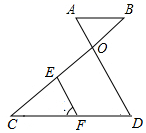 25. 2020年5月1日新版《北京市生活垃圾管理条例》实施,意味着北京市垃圾分类正式进入法治化、常态化、系统化轨道. 条例明确规定,将垃圾分为厨余垃圾、有害垃圾、其他垃圾和可回收物4类. 为了帮助同学们养成垃圾分类的好习惯,七年级一班计划以此为主题召开一次班会,需要一部分同学手绘可回收物的标识小卡片(如图).发给大家的纸张和样图中的纸张一样,都是边长为 cm的正方形.为了让大家画的标志在纸张中的位置大小尽可能的一致.标志中标注了A , B , C三个关键点,请你通过测量告诉大家A , B , C三点在纸张中的位置.
25. 2020年5月1日新版《北京市生活垃圾管理条例》实施,意味着北京市垃圾分类正式进入法治化、常态化、系统化轨道. 条例明确规定,将垃圾分为厨余垃圾、有害垃圾、其他垃圾和可回收物4类. 为了帮助同学们养成垃圾分类的好习惯,七年级一班计划以此为主题召开一次班会,需要一部分同学手绘可回收物的标识小卡片(如图).发给大家的纸张和样图中的纸张一样,都是边长为 cm的正方形.为了让大家画的标志在纸张中的位置大小尽可能的一致.标志中标注了A , B , C三个关键点,请你通过测量告诉大家A , B , C三点在纸张中的位置. 26. 在平面直角坐标系 中,已知点 , , ,…, , ,其中 , , ,…, , 为正整数.顺次连接 , , ,…, ,B的折线与x轴、y轴围成的封闭图形记为图形M.小明在求图形M的面积时,过点 , ,…, 作x轴的垂线,将图形M分成n个四边形,计算这些四边形面积的和,可以求出图形M的面积.
26. 在平面直角坐标系 中,已知点 , , ,…, , ,其中 , , ,…, , 为正整数.顺次连接 , , ,…, ,B的折线与x轴、y轴围成的封闭图形记为图形M.小明在求图形M的面积时,过点 , ,…, 作x轴的垂线,将图形M分成n个四边形,计算这些四边形面积的和,可以求出图形M的面积.
请你参考小明的思路,解决下面的问题.
(1)、当 时,①若 ,如图1,则图形M的面积为;
②用含有 , , 的式子表示图形M的面积为 .
(2)、当 时,从1,2,3,…,10这10个正整数中任选5个不同的数作为 .①小明选择了 ,请在图2中画出此时的图形M;
②在①的条件下,若小聪用剩下的5个数1,2,8,9,10作为 的取值,使新得到的图形M的面积与小明的图形M的面积相等,请直接写出这五个数的排序(写出一组即可).
27. 在平面直角坐标系中,M(a , b),N(c , d),对于任意的实数 ,我们称P(ka+kc , kb+kd)为点M和点N的k系和点.例如,已知M(2,3),N(1, ),点M和点N的2系和点为K(6,2).横、纵坐标都为整数的点叫做整点,已知A(1,2),B(2,0). (1)、点A和点B的 系和点的坐标为(直接写出答案);(2)、已知点C(m , 2),若点B和点C的k系和点为点D , 点D在第一、三象限的角平分线上.
(1)、点A和点B的 系和点的坐标为(直接写出答案);(2)、已知点C(m , 2),若点B和点C的k系和点为点D , 点D在第一、三象限的角平分线上.①求m的值;
②若点D为整点,且三角形BCD的内部(不包括边界)恰有3个整点,直接写出k的值;
(3)、若点E与点A关于x轴对称,点B向右平移一个单位得到点F , 点H为线段BF上的动点,点P为点A和点H的k系和点,点Q为点E和点H的k系和点,k>0,在点H运动过程中,若四边形AEQP的内部(不包括边界)都至少有10个整点,至多有15个整点,则k的取值范围为 .28. 已知:直线 ∥ ,A为直线 上的一个定点,过点A的直线交 于点B , 点C在线段BA的延长线上.D , E为直线 上的两个动点,点D在点E的左侧,连接AD , AE , 满足∠AED=∠DAE . 点M在 上,且在点B的左侧. (1)、如图1,若∠BAD=25°,∠AED=50°,直接写出∠ABM的度数;(2)、射线AF为∠CAD的角平分线.
(1)、如图1,若∠BAD=25°,∠AED=50°,直接写出∠ABM的度数;(2)、射线AF为∠CAD的角平分线.① 如图2,当点D在点B右侧时,用等式表示∠EAF与∠ABD之间的数量关系,并证明;
② 当点D与点B不重合,且∠ABM+∠EAF=150°时,直接写出∠EAF的度数 .