山西省太原市2021年中考数学一模试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算（﹣3）×（﹣1）的结果是（　　）

A、﹣4 B、﹣3 C、3 D、4

查看试题解析
2. 下列运算结果正确的是（　　）

A、（﹣a²）•a³＝a⁵ B、（a﹣5b）（a+5b）＝a²﹣5b² C、2x（x﹣5）＝2x²﹣10x D、x⁶÷x²＝x³

查看试题解析
3. 如图，将含30°角的直角三角板ABC放在平行线α和b上，∠C＝90°，∠A＝30°，若∠1＝20°，则∠2的度数等于（　　）

A、60° B、50° C、40° D、30°

查看试题解析
4. 小红同学对数据25，32，23，25，4■，43进行统计分析，发现“4■”的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（　　）

A、中位数 B、平均数 C、众数 D、方差

查看试题解析
5. 把不等式组 ${\begin{array}{l} x - 3 < 0 \\ \frac{x}{2} + 3 \geq 2 \end{array}$ 的解集表示在数轴上，正确的是（　　）

A、 B、 C、 D、

查看试题解析
6. 用配方法解方程x²﹣10x﹣1＝0时，变形正确的是（　　）

A、（x﹣5）²＝24 B、（x﹣5）²＝26 C、（x+5）²＝24 D、（x+5）²＝26

查看试题解析
7. 刘徽是我国三国时期杰出的数学大师，他的一生是为数学刻苦探究的一生，在数学理论上的贡献与成就十分突出，被称为“中国数学史上的牛顿”．刘徽精编了九个测量问题，都是利用测量的方法来计算高、深、广、远问题的，这本著作是（）．

A、《周髀算经》 B、《九章算术》 C、《孙子算经》 D、《海岛算经》

查看试题解析
8. 去年，面对严峻复杂的国内外环境，特别是疫情严重冲击，在以习近平同志为核心的党中央坚强领导下，我国经济社会发展主要目标任务完成情况好于预期，初步核算，全年国内生产总值约102万亿元，其中第三产业约占55%，由此可知，第三产业总值为（　　）

A、4.59×10¹³元 B、5.61×10¹⁴元 C、5.61×10¹³元 D、4.59×10¹⁴元

查看试题解析
9. 如图，小明在骑行过程中发现山上有一建筑物．他测得仰角为15°；沿水平笔直的公路向山的方向行驶4千米后，测得该建筑物的仰角为30°，若小明的眼睛与地面的距离忽略不计，则该建筑物离地面的高度为（　　）

A、2 $\sqrt{3}$ 千米 B、2 $\sqrt{2}$ 千米 C、2千米 D、 $\frac{3 \sqrt{3}}{2}$ 千米

查看试题解析
10. 如图，AB是半圆O的直径，点C为半圆上的一点，点D为AO上一点，AB＝8，∠B＝60°，△DB'C与△DBC关于直线DC对称，连接B'O交半圆于点E若B'C与半圆相切，则图中阴影部分的面积等于（　　）

A、3π﹣4 $\sqrt{2}$ B、2π﹣4 $\sqrt{2}$ C、3π﹣8 D、8﹣2π

查看试题解析

二、填空题

11. 化简（x﹣1）²﹣x²的结果是．

查看试题解析
12. 在物理实验课上，同学们用三个开关，两个灯泡、一个电源及若干条导线连接成如图所示的电路图，随机闭合图中的两个开关，有一个灯泡发光的概率是．

查看试题解析
13. 如图，∠PAQ＝36°，点B为射线AQ上一点，AB＝5cm ，按以下步骤作图，第一步：分别以点A ， B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧相交于点M ， N；第二步：作直线MN交射线AP于点D ，连接BD；第三步：以点B为圆心，BA的长为半径画弧，交射线AP于点C ，连接BC ，线段CD的长为cm ．

查看试题解析
14. 某体育器材商场以a元/台的价格购进一种家用健身器材，提价60%作为标价后，为了迎合消费者的心理，再按八折促销，在不考虑其他因素的前提下，每售出一台该器材商场可获利元．

查看试题解析
15. 如图，在▱ABCD中，AD＝6，对角线BD⊥CD ， ∠BAD＝30°，∠BAD与∠CDB的平分线交于点E ，延长DB到点F ，使DF＝AD ，连接EF ，则EF的长为．

查看试题解析

三、解答题

16.

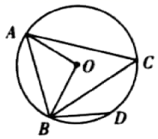
(1)、计算：（﹣ $\frac{1}{3}$ ）^-2+ $\sqrt{18}$ sin45°﹣（﹣4+2）² ，

(2)、化简再求值： $(\frac{3}{x^{2} - 9} + \frac{1}{x + 3}) \div \frac{x}{x - 3}$ ，其中x＝﹣3+ $\sqrt{3}$ ．

查看试题解析
17. 正比例函数y＝kx与反比例函数y＝ $\frac{k}{x}$ 的图象相交于A ， B两点，已知点A的横坐标为1，点B的纵坐标为﹣3．

(1)、直接写出A ， B两点的坐标；

(2)、求这两个函数的表达式．

查看试题解析
18. 如图，⊙O是△ABC的外接圆，∠AOB＝96°，∠CAB＝60°，点D是 $\overset{⌢}{B C}$ 的中点．求∠ABD的度数．

查看试题解析
19. 为丰富同学们的生活体验，学校计划引进“晋式传统刺绣，仕女面塑艺术，唐风篆刻，汉风传统彩绘艺术”四个太原市非物质文化遗产项目，为学生提供课后服务，要求每名学生必须且只能选定其中一个项目，在开学第一周，随机抽取部分学生进行了问卷调查，为了方便统计，这四个项目依次用字母A ， B ， C ， D标记，将结果绘制出如图所示的扇形统计图和条形统计图（不完整），结合图中信息解答下列问题：

(1)、被调查的学生共有人；在扇形统计图中，B所对应的圆心角的度数为；

(2)、补全条形统计图；

(3)、已知该校有1600学生，请估计选定“汉风传统彩绘艺术”项目的人数．

查看试题解析
20. 太原市是山西省政府命名的“山西省园林城市”，从2018年起，我市围绕“一核”“三圈”，以“两个百万亩森林建设”为重点建设十大骨干工程，到2018年底，林地面积约350万亩，为持续保护和改善生态环境，建设整洁、优美、宜居的现代化城市，再现锦绣太原城盛景，经过两年的努力，到2020年底我市林地面积约423.5万亩．

(1)、求这两年林地面积的年平均增长率；

(2)、若要实现到2021年底林地面积至少为508.2万亩的目标，求2021年林地面积的增长率不低于多少．

查看试题解析

21. 某养殖场需要定期购买饲料，已知该养殖场每天需要200千克饲料，饲料的价格为1.8元/千克，饲料的保管费与其他费用平均每天为0.05元/千克，购买饲料每次的运费为180元．

任务1：该养殖场多少天购买一次饲料才能使平均每天支付的总费用最少；

小明的分析如下：如果2天购买一次，则保管费与其他费用需支付200×0.05＝10（元）；如果3天购买一次，则保管费与其他费用需支付200×2×0.05+200×0.05＝30（元）；如果4天购买一次，则保管费与其他费用需支付200×3×0.05+200×2×0.05+200×0.05＝60（元），他发现已有的数学模型不能解决这个问题，想到了用函数图象的方法解决，设x天购买一次饲料，平均每天支付的总费用为y元，下面是他解决这个问题的过程，请解答相关问题．

(1)、计算得到x与y的部分对应值如下表，请补全表格；

x/天	…	2	3	4	5	6	7	8	9	10	…
Y/元	…	455.0	430.0	420.0			415.7	417.5	420.0	423.0	…

(2)、在平面直角坐标系中，描出（1）中所对应的点；

(3)、结合图象：养殖场天购买一次饲料才能使平均每天支付的总费用最少．

任务2：提供饲料的公司规定，当一次购买饲料不少于2000千克时，价格可享受九折优惠，在该养殖场购买饲料时是否需要考虑这一优惠条件，简要说明理由．

查看试题解析

22. 综合与探究
问题情境

在Rt△ABC中，∠BAC＝90°，AB＝AC ，点D是射线BC上一动点，连接AD ，将线段AD绕点A逆时针旋转90°至AE ，连接DE ， CE ．

(1)、探究发现

如图1，BD＝CE ， BD⊥CE ，请证明；探究猜想；

(2)、如图2，当BD＝2DC时，猜想AD与BC之间的数量关系，并说明理由；

(3)、探究拓广
当点D在BC的延长线上时，探究并直接写出线段BD ， DC ， AD之间的数量关系．

查看试题解析
23. 综合与实践
如图1，抛物线y＝﹣ $\frac{8}{3}$ x²﹣ $\frac{9}{4}$ x+6与x轴交于点A和点B（点A在点B的左侧），与y轴交于点C ．

(1)、求直线AC的表达式；

(2)、点E在抛物线的对称轴上，在平面内是否存在点F ，使得以点A ， C ， E ， F为顶点的四边形是矩形？若存在，请直接写出点E的坐标；若不存在，请说明理由；

(3)、如图2，设点P从点O出发以1个单位长度/秒的速度向终点A运动，同时点Q从点A出发以 $\frac{5}{4}$ 个单位长度/秒的速度向终点C运动，运动时间为t秒，当∠OPQ的平分线恰好经过OC的中点时，求t的值．

查看试题解析