山东省济宁市泗水县2021年中考数学一模试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. -4的绝对值是（）

A、-4 B、 $- \frac{1}{4}$ C、4 D、 $\frac{1}{4}$

查看试题解析
2. 在中国共产党的坚强领导下，我国有效控制了新冠疫情．而截至2021年3月25日，全球新冠肺炎确诊人数高达1.26亿，其中数据1.26亿用科学记数法可表示为（）

A、 $0.126 \times 10^{8}$ B、 $1.26 \times 10^{8}$ C、 $1.26 \times 10^{9}$ D、 $12.6 \times 10^{9}$

查看试题解析
3. 下列计算正确的是（　　）

A、x⁴+x⁴＝2x⁸ B、（x²y）³＝x⁶y³ C、x²x³＝x⁶ D、(x﹣y）（y﹣x）＝x²﹣y²+2xy

查看试题解析
4. 如图所示，将含有30°角的三角板（∠A＝30°）的直角顶点放在相互平行的两条直线其中一条上，若∠1＝39°，则∠2的度数（　　）

A、21° B、31° C、39° D、51°

查看试题解析
5. 如图， $A B$ 为 $⊙ O$ 的直径，点C、点D是 $⊙ O$ 上的两点，连接 $C A$ ， $C D$ ， $A D$ ．若 $∠ C A B = 35 °$ ，则 $∠ A D C$ 的度数是（）

A、40° B、45° C、55° D、100°

查看试题解析
6. 某社团成员的年龄（单位：岁）如下：

年龄

12

13

14

15

16

人数

1

2

2

3

1

他们年龄的众数和中位数分别是（　　）

A、16，15 B、16，14 C、15，15 D、15，14

查看试题解析
7. 若抛物线y＝(x－m)²＋(m＋1)的顶点在第一象限，则m的取值范围为（）

A、m＞1 B、m＞0 C、m＞－1 D、－1＜m＜0

查看试题解析
8. 设a、b是方程x²＋x－2021＝0的两个实数根，则a²+ab＋2a＋b的值是（　　）

A、2020 B、2021 C、-1 D、-2

查看试题解析
9. 如图，一次函数 $y_{1} = a x + b$ 和反比例函数 $y_{2} = - \frac{4}{x}$ 的图象交于 $A (m ， 1)$ ， $B (n ， - 2)$ 两点，若当 $y_{1} < y_{2}$ 时，则x的取值范围是（）

A、 $x < - 4$ 或 $0 < x < 2$ B、 $- 4 < x < 0$ 或 $x > 2$ C、 $x > 1$ 或 $- 2 < x < 0$ D、 $x < - 2$ 或 $x > 1$

查看试题解析
10. 将一列有理数﹣1，2，﹣3，4，﹣5，6，……，如图所示有序排列．根据图中的排列规律可知，有理数4在“峰1”中C的处．则有理数-2021在（）

A、峰403 E处 B、峰403 D处 C、峰404 D处 D、峰404 E处

查看试题解析

二、填空题

11. 函数y＝ $\frac{\sqrt{5 - x}}{x - 3}$ 中自变量x的取值范围是．

查看试题解析
12. 分解因式：x³﹣4xy²= ．

查看试题解析
13. 已知整数a满足 $1 < a \leq 3$ ，则分式 $(1 - \frac{2}{a}) \cdot \frac{a}{a^{2} - 4}$ 的值为．

查看试题解析
14. 如图，在平面直角坐标系xOy中，点A、C、F在坐标轴上，E是OA的中点，四边形AOCB是矩形，四边形BDEF是正方形，若点C的坐标为 $(3 \sqrt{3} ， 0)$ ，则点E的坐标为．

查看试题解析
15. 如图，在矩形ABCD中，E是AD边的中点，BE⊥AC ，垂足为点F ，连接DF ，下面四个结论：①△AEF∽△CBF；②CF＝2AF；③DF＝DC；④S_{四边形CDEF}＝ $\frac{5}{2}$ S_△ABF ．其中正确的结论有．

查看试题解析

三、解答题

16. 计算：|2﹣tan60°|﹣ ${(π - 3.14)}^{0}$ ＋ $\frac{1}{2} \sqrt{12}$ ＋ ${(- \frac{1}{2})}^{- 2}$

查看试题解析
17. 如图，在等腰△ABC中，AB=AC ， ∠A=36°，点D、E分别为AB、AC上的点，将∠A沿直线DE翻折，使点A落在点C处．

(1)、用尺规作图作出直线DE；(要求：尺规作图，保留作图痕迹，不写作法)

(2)、若AD= $\sqrt{5}$ ，求BC的长．

查看试题解析
18. 主题班会课上，王老师出示了如图所示的一幅漫画，经过同学们的一番热议，达成以下四个观点：
A．放下自我，彼此尊重； B．放下利益，彼此平衡；
C．放下性格，彼此成就； D．合理竞争，合作双赢．
要求每人选取其中一个观点写出自己的感悟，根据同学们的选择情况，小明绘制了下面两幅不完整的图表，请根据图表中提供的信息，解答下列问题：
观点
频数
频率
A
a
0.2
B
12
0.24
C
8
b
D
20
0.4

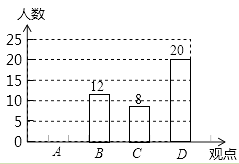(1)、参加本次讨论的学生共有人；

(2)、表中a= ， b=；

(3)、将条形统计图补充完整；

(4)、现准备从A，B，C，D四个观点中任选两个作为演讲主题，请用列表或画树状图的方法求选中观点D（合理竞争，合作双赢）的概率．

查看试题解析
19. 学校准备购进一批节能灯，已知1只A型节能灯和3只B型节能灯共需26元；3只A型节能灯和2只B型节能灯共需29元．

(1)、求一只A型节能灯和一只B型节能灯的售价各是多少元；

(2)、学校准备购进这两种型号的节能灯共50只，并且A型节能灯的数量不多于B型节能灯数量的3倍，请设计出最省钱的购买方案，并说明理由．

查看试题解析
20. 如图，在△ABC中，AB＝AC ， AD⊥BC于点D ，过点C作⊙O与边AB相切于点E ，交BC于点F ， CE为⊙O的直径．

(1)、求证：OD⊥CE；

(2)、若DF＝1，DC＝3，求AE的长．

查看试题解析
21. （数学经验）三角形的中线的性质：三角形的中线等分三角形的面积．

(1)、（经验发展）面积比和线段比的联系：
如图1，M为△ABC的AB上一点，且BM=2AM ．若△ABC的面积为a ，若△CBM的面积为S ，则S=(用含a的代数式表示)．

(2)、（结论应用）如图2，已知△CDE的面积为1， $\frac{C D}{A C} = \frac{1}{4}$ ， $\frac{C E}{C B} = \frac{1}{3}$ ，求△ABC的面积．

(3)、（迁移应用）如图3．在△ABC中，M是AB的三等分点( $A M = \frac{1}{3} A B$ )，N是BC的中点，若△ABC的面积是1，请直接写出四边形BMDN的面积为．

查看试题解析
22. 如图，已知抛物线y＝x²+bx+c过A ， B ， C三点，已知点A(3，0)，点C(0，﹣3)．

(1)、求抛物线解析式及点B的坐标；

(2)、点D为抛物线的对称轴上一点，求 $| D A - D C |$ 的最大值及此时点D的坐标；

(3)、点P为抛物线上一动点，是否存在点P使得∠PCA＝15°，若存在，请求出点P的横坐标．若不存在，请说明理由．

查看试题解析

年龄	12	13	14	15	16
人数	1	2	2	3	1

观点	频数	频率
A	a	0.2
B	12	0.24
C	8	b
D	20	0.4