辽宁省沈阳市于洪区2021年中考数学一模试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. 下列各数是无理数的是( )A、﹣3 B、0 C、π D、2. 伴随“互联网+”时代的来临,预计到2025年,我国各类网络互助平台的实际参与人数将达到450000000,将数据450000000用科学记数法表示为( )A、4.5×108 B、4.5×109 C、45×107 D、0.45×10103. 如图,是由五个相同的小立方块搭成的几何体,这个几何体的左视图是( )
 A、
A、 B、
B、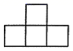 C、
C、 D、
D、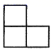 4. 下列计算正确的是( )A、a6÷a2=a3 B、a2+2a=3a3 C、(﹣2ab2)3=﹣8a3b6 D、(2a+b)2=4a2+b25. 下列说法正确的是( )A、一组数据1,3,5,3,4的中位数是5 B、为了解全国中小学生的心理健康状况,应选用普查方式 C、“买中奖率为 的奖券10张,中奖”是必然事件 D、若甲、乙两人六次跳远成绩平均数相同,S2甲=0.1,S2乙=0.3,则甲的成绩较稳定6. 计算 的结果是( )A、x﹣2 B、 C、 D、7. 若m ﹣2,则一次函数 的图象可能是( )A、
4. 下列计算正确的是( )A、a6÷a2=a3 B、a2+2a=3a3 C、(﹣2ab2)3=﹣8a3b6 D、(2a+b)2=4a2+b25. 下列说法正确的是( )A、一组数据1,3,5,3,4的中位数是5 B、为了解全国中小学生的心理健康状况,应选用普查方式 C、“买中奖率为 的奖券10张,中奖”是必然事件 D、若甲、乙两人六次跳远成绩平均数相同,S2甲=0.1,S2乙=0.3,则甲的成绩较稳定6. 计算 的结果是( )A、x﹣2 B、 C、 D、7. 若m ﹣2,则一次函数 的图象可能是( )A、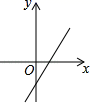 B、
B、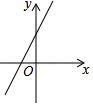 C、
C、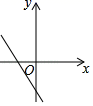 D、
D、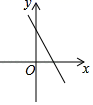 8. 如图,正六边形ABCDEF内接于⊙O , 边长AB=2,则扇形AOB的面积为( )
8. 如图,正六边形ABCDEF内接于⊙O , 边长AB=2,则扇形AOB的面积为( ) A、 B、 C、π D、9. 如图,四边形ABCD是平行四边形,以点A为圆心、AB的长为半径画弧交AD于点F,再分别以点B,F为圆心、大于 BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )
A、 B、 C、π D、9. 如图,四边形ABCD是平行四边形,以点A为圆心、AB的长为半径画弧交AD于点F,再分别以点B,F为圆心、大于 BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )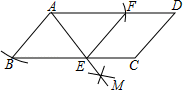 A、BE=EF B、EF∥CD C、AE平分∠BEF D、AB=AE10. 若点A(﹣1,y1),B(2,y2),C(3,y3)在抛物线y=﹣2x2+8x+c的图象上,则y1 , y2 , y3的大小关系是( )A、y3<y2<y1 B、y2<y1<y3 C、y1<y3<y2 D、y3<y1<y2
A、BE=EF B、EF∥CD C、AE平分∠BEF D、AB=AE10. 若点A(﹣1,y1),B(2,y2),C(3,y3)在抛物线y=﹣2x2+8x+c的图象上,则y1 , y2 , y3的大小关系是( )A、y3<y2<y1 B、y2<y1<y3 C、y1<y3<y2 D、y3<y1<y2二、填空题
-
11. 因式分解: = .12. 一个多边形的内角和是 ,那么这个多边形是 .13. 在一个不透明的袋子里有若干个白球,为估计白球个数,小东向其中投入10个黑球(与白球除颜色外均相同),搅拌均匀后随机摸出一个球,记下颜色,再把它放入袋中,不断重复这一过程,共摸球100次,发现有25次摸到黑球.请你估计这个袋中有个白球.14. 如图,在平面直角坐标系中,正比例函数y=kx与反比例函数 的图象相交于A , B两点,过点A作y轴的垂线交y轴于点C , 连接BC , 则△ABC的面积是 .
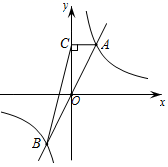 15. 如图1,在矩形ABCD中,点E在CD上,∠AEB=90°,点P从点A出发,沿A→E→B的路径匀速运动到点B停止,作PQ⊥CD于点Q , 设点P运动的路程为x , PQ长为y , 若y与x之间的函数关系图象如图2所示,当x=12时,PQ的长是 .
15. 如图1,在矩形ABCD中,点E在CD上,∠AEB=90°,点P从点A出发,沿A→E→B的路径匀速运动到点B停止,作PQ⊥CD于点Q , 设点P运动的路程为x , PQ长为y , 若y与x之间的函数关系图象如图2所示,当x=12时,PQ的长是 . 16. 如图,△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点B逆时针旋转一定的角度α(0°<α<90°),直线A1C1分别交AB , AC于点G , H . 当△AGH为等腰三角形时,则CH的长为 .
16. 如图,△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点B逆时针旋转一定的角度α(0°<α<90°),直线A1C1分别交AB , AC于点G , H . 当△AGH为等腰三角形时,则CH的长为 .
三、解答题
-
17. 计算:2cos30°+(﹣ )﹣2+|5﹣ |﹣(π﹣3.14)0 .18. 甲、乙两人去超市选购奶制品,有两个品牌的奶制品可供选购,其中蒙牛品牌有三个种类的奶制品:A:纯牛奶,B:酸奶,C:核桃奶;伊利品牌有两个种类的奶制品:D:纯牛奶,E:核桃奶.(1)、甲从这两个品牌的奶制品中随机选购一种,选购到纯牛奶的概率是;(2)、若甲喜爱蒙牛品牌的奶制品,乙喜爱伊利品牌的奶制品,甲、乙两人从各自喜爱的品牌中随机选购一种奶制品,请用列表法或画树状图法求出两人选购到同一种类奶制品的概率.19. 已知:如图,在四边形ABCD中,AD BC , ∠A=90°,BD=BC , CE⊥BD于点E .
 (1)、求证:AD=EB;(2)、若∠DCE=15°,AB=2,请直接写出DE的长.20. 网络学习越来越受到学生的青睐,某校为学生提供了四种课后辅助学习方式:A网上测试,B网上阅读,C网上答疑,D网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,被调查学生需从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如图两幅不完整的统计图:
(1)、求证:AD=EB;(2)、若∠DCE=15°,AB=2,请直接写出DE的长.20. 网络学习越来越受到学生的青睐,某校为学生提供了四种课后辅助学习方式:A网上测试,B网上阅读,C网上答疑,D网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,被调查学生需从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如图两幅不完整的统计图:根据统计图提供的信息,解答下列问题:
 (1)、本次共调查了名学生;(2)、在扇形统计图中,m的值是 , D对应的扇形圆心角的度数是度;(3)、根据以上信息直接在答题卡中补全条形统计图;(4)、根据抽样调查的结果,请你估计该校800名学生中最喜欢方式D的学生人数.21. 某零件生产厂生产的某型号零件1月份平均日产量为2000个,由于市场需求量大增,工厂决定从2月份起扩大产能,3月份平均日产量达到2420个.假设该型号零件2,3,4每个月平均日产量增长率相同.(1)、求该型号零件日产量的月平均增长率;(2)、预计4月份该型号零件平均日产量为多少个?22. 如图,AB与⊙O相切于点B , AO交⊙O于点C , AO的延长线交⊙O于点D , E是 上不与B , D重合的点,sinA= .
(1)、本次共调查了名学生;(2)、在扇形统计图中,m的值是 , D对应的扇形圆心角的度数是度;(3)、根据以上信息直接在答题卡中补全条形统计图;(4)、根据抽样调查的结果,请你估计该校800名学生中最喜欢方式D的学生人数.21. 某零件生产厂生产的某型号零件1月份平均日产量为2000个,由于市场需求量大增,工厂决定从2月份起扩大产能,3月份平均日产量达到2420个.假设该型号零件2,3,4每个月平均日产量增长率相同.(1)、求该型号零件日产量的月平均增长率;(2)、预计4月份该型号零件平均日产量为多少个?22. 如图,AB与⊙O相切于点B , AO交⊙O于点C , AO的延长线交⊙O于点D , E是 上不与B , D重合的点,sinA= . (1)、求∠DEB的度数;(2)、若⊙O的半径为2,点F在AB的延长线上,且BF=2 ,求证:DF与⊙O相切.23. 如图,在平面直角坐标系中,直线l1:y= x+ 与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B .
(1)、求∠DEB的度数;(2)、若⊙O的半径为2,点F在AB的延长线上,且BF=2 ,求证:DF与⊙O相切.23. 如图,在平面直角坐标系中,直线l1:y= x+ 与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B .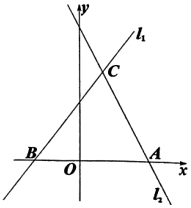 (1)、求直线l2的表达式;(2)、点P是直线l2上的一个动点,过点P作EF⊥x轴于点E , 交直线l1于点F ,
(1)、求直线l2的表达式;(2)、点P是直线l2上的一个动点,过点P作EF⊥x轴于点E , 交直线l1于点F ,①若PF=AB , 求点P的坐标.
②过点P作PQ⊥l1于点Q , 若PQ=2PE , 请直接写出点P的坐标.
24. 正方形ABCD , 点E在射线CD上,连接AE , 以AE为斜边,作Rt△AEF , FE=FA(点F , B在直线AE的两侧),连接DF . (1)、如图,点E在线段CD上.
(1)、如图,点E在线段CD上.①求∠ADF的度数.
②求证:CE= DF .
(2)、若DE=2,以A , E , D , F为顶点的四边形的面积为6时,请直接写出DF的长.25. 在平面直角坐标系中,抛物线y=ax2+bx﹣7(a≠0)经过点P(3,8),与x轴交于点A , B(7,0),对称轴直线l交x轴于点M , 过点C(3,0)作射线CD交直线l于点D(D在x轴上方),AE CD交直线l于点E , EF x轴交射线CD于点F . (1)、求抛物线的表达式;(2)、如图,当MD为何值时,点F恰好落在该抛物线上?(3)、当MD=1时,过点F作FG⊥x轴于点G , 点H为射线FG上一点,连接CE , 当直线AH与直线CE的夹角为45°时,请直接写出FH的长.
(1)、求抛物线的表达式;(2)、如图,当MD为何值时,点F恰好落在该抛物线上?(3)、当MD=1时,过点F作FG⊥x轴于点G , 点H为射线FG上一点,连接CE , 当直线AH与直线CE的夹角为45°时,请直接写出FH的长.