辽宁省沈阳市和平区2021年中考数学一模试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中比1大比2小的无理数是（　　　）

A、1.414 B、 $\sqrt{2}$ C、 $\frac{3}{2}$ D、 $\sqrt{5}$

查看试题解析
2. 如图是由7个相同的小立方块搭成的几何体这个几何体的俯视图是（　　　）

A、 B、 C、 D、

查看试题解析
3. 下列事件中，是不可能事件的是（　　　）

A、打开电视，正在播放《新闻联播》 B、如果x²=y² ，那么x=y C、直线外一点与直线上各点连接的所有线段中，垂线段最短 D、从一个只有黑球的盒子里面摸出一个球是白球

查看试题解析
4. 下列关于数字变换的图案中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 下列计算结果正确的是（　　　）

A、 $\frac{3}{x - 2} + \frac{2}{2 - x} = \frac{1}{x - 2}$ B、 ${(x^{2})}^{3} = x^{5}$ C、 ${(- x y)}^{5}$ ÷ ${(- x y)}^{3}$ = $- x^{2} y^{2}$ D、 $3 x^{2} y - 5 x y^{2} = - 2 x y$

查看试题解析
6. 如图，AB∥CD ， FE⊥DB于点E ， ∠1=48°，则∠2的大小为（　　　）

A、52° B、48° C、42° D、30°

查看试题解析
7. 不等式组 ${\begin{array}{l} 2 (x - 1) < 0 \\ 3 x + 1 \geq 2 x \end{array}$ 的解集在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
8. 2020年，我国国内生产总值约为1015986亿元，将数据1015986亿用科学记数法表示为（　　　）

A、1.015986×10¹⁵ B、1.015986×10¹⁴ C、1.015986×10¹³ D、1.015986×10¹²

查看试题解析
9. 反比例函数y $= \frac{- 5}{x}$ （x＞0）的图象在（　　　）

A、第一、三象限 B、第二、四象限 C、第一象限 D、第四象限

查看试题解析
10. 在平面直角坐标系中，△ABC与△A₁B₁C₁的相似比是2：1，并且是关于原点O的位似图形，若点B的坐标为（﹣4，﹣2），则其对应点B₁的坐标是（　　　）

A、（﹣2，﹣1） B、（2，1） C、（﹣2，﹣1）或（2，1） D、（﹣8，﹣4）

查看试题解析

二、填空题

11. 因式分解：2m²﹣2= ．

查看试题解析
12. 一个多边形的内角和是它的外角和的4倍，则这个多边形的边数是．

查看试题解析
13. 已知△ABC～△DEF ， AB：DE=3：5，△ABC的面积为9，则△DEF的面积为．

查看试题解析
14. 数据5，2，2，3，1，5，4的众数是．

查看试题解析
15. 如图，由边长为1的小正方形构成的网格中，点A ， B ， C都在格点上，以AB为直径的圆经过点C ， D ，则tan∠ADC的值为．

查看试题解析
16. 如图，在四边形ABCD中，∠DAB=∠BCD=90°，对角线AC与BD相交于点E ，点F ， G分别是AC ， BD的中点，当∠CBD=15°，EG=EC ， FG $= \sqrt{3}$ 时，则线段AC的长为．

查看试题解析

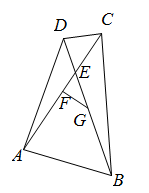
三、解答题

17. 计算：2sin60°﹣| $\sqrt{3} -$ 2|﹣2021⁰ $- \sqrt{12} -$ （ $- \frac{1}{3}$ ）^﹣1 ．

查看试题解析
18. 在一个不透明的袋中装有除颜色外完全相同的1个红球和2个黄球（可记作黄1，黄2）．

(1)、小明从袋中随机摸出1个球，记下颜色后放回混合均匀后再从中随机摸出1个球，并记录下颜色请用画树状图或列表法，求小明第一次摸到黄球，第二次摸到红球的概率；

(2)、小华从袋中随机摸出1个球，记下颜色后不放回，再从剩余的球中随机摸出1个球，并记录下颜色请直接写出小华两次摸到的球中有1个黄球，1个红球的概率是．

查看试题解析
19. 如图，在矩形ABCD中，对角线AC与BD相交于点E ，过点A作AF∥BD ，过点B作BF∥AC ，两线相交于点F ．

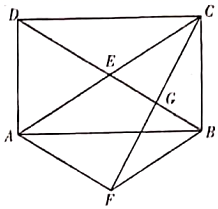(1)、求证：四边形AEBF是菱形；

(2)、连接CF ，交BD于点G ，若BD⊥CF ，请直接写出∠AED的度数为度．

查看试题解析
20. 某校为调查学生对数学史知识的了解情况，从全校学生中随机抽取n名学生进行测试，测试成绩进行整理后分成五组，并绘制成如下不完整的频数直方图和扇形统计图．请根据图中信息解答下列问题：

(1)、本次调查共抽测了名学生，并直接在答题卡中补全频数直方图；

(2)、在扇形统计图中m的值是， 70﹣80所对应的扇形圆心角的度数是度；

(3)、已知“80﹣90”这组的数据如下：82，83，83，85，85，85，86，87，88，88，88，89，抽取的n名学生测试成绩的中位数是分；

(4)、若成绩达到60分以上（含60分）为合格，请你估计该校2000名学生中有多少名学生对数学史知识了解情况为合格．

查看试题解析
21. 药店购进一批口罩进行销售，进价为每盒40，如果按照每盒47元的价格进行销售，每月可以售出200盒经过市场调查发现，每盒口罩售价每涨价1元，其月销售量就将减少10盒．

(1)、药店要保证每月销售此种口罩盈利1700元，又要使每盒售价不高于55元，则每盒口罩可涨价多少元？

(2)、若使该口罩的月销量不低于150盒，则每盒口罩的售价应不高于多少元？

查看试题解析
22. 如图一面墙上有一个矩形门ABCD现要打掉部分墙体将它改为一个圆弧形的门，在圆内接矩形ABCD中，AD $= \sqrt{3}$ m ， CD=1m ．

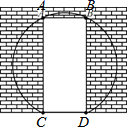(1)、求此圆弧形门所在圆的半径是多少m？

(2)、求要打掉墙体的面积是多少m²？（π≌3.1， $\sqrt{3} \approx$ 1.7，结果精确到1m²）

查看试题解析
23. 如图，在平面直角坐标系中，△ABO的顶点O是坐标原点，点A的坐标为（﹣30，0），点B的坐标为（﹣30，30），△CDE是位于y轴的左侧且边长为8 $\sqrt{3}$ 的等边三角形，边DE垂直于x轴，△CDE从点C与点O重合的位置开始，以每秒2个单位长的速度先沿点O到点A的方向向左平移，当DE边与直线AB重合时，继续以同样的速度沿点A到点B的方向向上平移，当点D与点B重合时，△CDE停止移动．

(1)、求直线OB的函数表达式；

(2)、当△CDE移动3秒时，请直接写出此时点C的坐标为；

(3)、在△CDE的平移过程中，连接AE ， AC ，当△ACE的面积为36 $\sqrt{3}$ 时，请直接写出此时点E的坐标为．

查看试题解析
24. 在正方形ABCD中，点M是边CD上一点，点N是边AD上一点，连接BM ， CN相交于点P ，且CM=DN ．

(1)、如图1，请判断线段BM与CN的数量关系和位置关系，并证明你的结论；

(2)、如图2，延长CN到点Q ，连接DQ ，且∠CQD=45°．
①请直接写BP ， CP ， CQ之间的数量关系为；

②连接AC ， AQ ，当BP=2CP ， △ACQ的面积是6时，请直接写出NQ的长为；

(3)、点E在线段CN上，连接BE ， DE ，当AB $= \sqrt{6}$ ，∠BED=135°，BE $+ \sqrt{2}$ DE=3 $\sqrt{2}$ 时，请直接写出NE的长为．

查看试题解析
25. 如图，抛物线y=a $x^{2}$ +bx $- \frac{20}{9}$ ，交y轴于点A ，交x轴于B（﹣1，0），C（5，0）两点，抛物线的顶点为D ，连接AC ， CD ．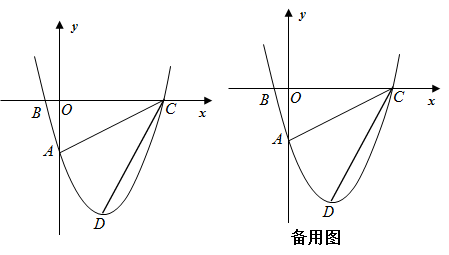

(1)、求直线AC的函数表达式；

(2)、求抛物线的函数表达式及顶点D的坐标；

(3)、过点D作x轴的垂线交AC于点G ，点H为线段CD上一动点，连接GH ，将△DGH沿GH翻折到△GHR（点R ，点G分别位于直线CD的两侧），GR交CD于点K ，当△GHK为直角三角形时．
①请直接写出线段HK的长为；

②将此Rt△GHK绕点H逆时针旋转，旋转角为α（0°＜α＜180°），得到△MHN ，若直线MN分别与直线CD ，直线DG交于点P ， Q ，当△DPQ是以PQ为腰的等腰三角形时，请直接写出点P的纵坐标为．

查看试题解析