河北省遵化市2021年中考数学一模试卷
试卷更新日期:2021-05-25 类型:中考模拟
一、单选题
-
1. 2019的相反数是( )A、 B、﹣ C、|2019| D、﹣20192. 下列各式中,计算正确的是( )A、 B、 C、 D、3. 某路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小明到达该路口时,遇到绿灯的概率是( )A、 B、 C、 D、4. 下列因式分解正确的是( )A、 B、 C、 D、5. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确的是( )A、 B、 C、 D、6. 若 ,且 ,则 的值是( )A、4 B、2 C、20 D、147. 解分式方程 时,去分母变形正确的是( )A、 B、 C、 D、8. 若关于x的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、9. 语句“x的 与x的和不超过5”可以表示为( )A、 +x≤5 B、 +x≥5 C、 ≤5 D、 +x=510. 如图所示是一个几何体的三视图,如果一只蚂蚁从这个几何体的点 出发,沿表面爬到 的中点 处,则最短路线长为( )
 A、 B、 C、 D、11. 如图,在平面直角坐标系中,将边长为1的正方形OABC绕点О顺时针旋转45°后得到正方形OA1B1C1 , 依此方式,绕点O连续旋转2019次得到正方形OA2019B2019C2019那么点A2019的坐标是( )
A、 B、 C、 D、11. 如图,在平面直角坐标系中,将边长为1的正方形OABC绕点О顺时针旋转45°后得到正方形OA1B1C1 , 依此方式,绕点O连续旋转2019次得到正方形OA2019B2019C2019那么点A2019的坐标是( ) A、( ,- ) B、(1,0) C、(- , ) D、(0,-1)12. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )
A、( ,- ) B、(1,0) C、(- , ) D、(0,-1)12. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )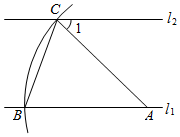 A、 B、 C、 D、13. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形AECF的面积为20,DE=2,则AE的长为( )
A、 B、 C、 D、13. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形AECF的面积为20,DE=2,则AE的长为( )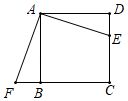 A、4 B、 C、6 D、14. 如图,在 中, , ,AD是斜边BC上的中线,将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于( )
A、4 B、 C、6 D、14. 如图,在 中, , ,AD是斜边BC上的中线,将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于( )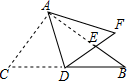 A、120° B、108° C、72° D、36°15. 平面直角坐标系中,已知▱ABCD的三个顶点坐标分别是A(m,n),B ( 2,-l ),C(-m,-n),则点D的坐标是( )A、(-2 ,1 ) B、(-2,-1 ) C、(-1,-2 ) D、(-1,2 )16. 如图,在Rt△ABC中,∠ABC=90°,AB= ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A、120° B、108° C、72° D、36°15. 平面直角坐标系中,已知▱ABCD的三个顶点坐标分别是A(m,n),B ( 2,-l ),C(-m,-n),则点D的坐标是( )A、(-2 ,1 ) B、(-2,-1 ) C、(-1,-2 ) D、(-1,2 )16. 如图,在Rt△ABC中,∠ABC=90°,AB= ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )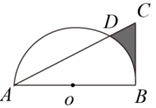 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
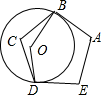
17. 计算 的结果是.18. 如图, 与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧 所对的圆心角 的大小为度.
 19. 有2019个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.如果第一个数是0,第二个数是1,那么前6个数的和是 , 这2019个数的和是.
19. 有2019个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.如果第一个数是0,第二个数是1,那么前6个数的和是 , 这2019个数的和是.三、解答题
-
20. 先化简,再求值 ,其中 满足
21. 已知:如图,在平行四边形ABCD中,AE⊥BC , CF⊥AD , E , F分别为垂足.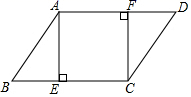 (1)、求证:△ABE≌△CDF;(2)、求证:四边形AECF是矩形.22. 如图,一次函数y=kx+b的图象与反比例函数 的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
(1)、求证:△ABE≌△CDF;(2)、求证:四边形AECF是矩形.22. 如图,一次函数y=kx+b的图象与反比例函数 的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.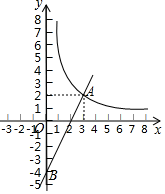 (1)、求函数 和y=kx+b的解析式;(2)、结合图象直接写出不等式组0< <kx+b的解集.23. “扫黑除恶”受到广大人民的关注,某中学对部分学生就“扫黑除恶”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)、求函数 和y=kx+b的解析式;(2)、结合图象直接写出不等式组0< <kx+b的解集.23. “扫黑除恶”受到广大人民的关注,某中学对部分学生就“扫黑除恶”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题: (1)、接受问卷调查的学生共有人,扇形统计图中“很了解”部分所对应扇形的圆心角为;(2)、请补全条形统计图;(3)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.24. 如图, ,DB平分∠ADC,过点B作 交AD于M.连接CM交DB于N.
(1)、接受问卷调查的学生共有人,扇形统计图中“很了解”部分所对应扇形的圆心角为;(2)、请补全条形统计图;(3)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.24. 如图, ,DB平分∠ADC,过点B作 交AD于M.连接CM交DB于N.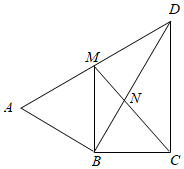 (1)、求证: ;(2)、若 ,求MN的长.
(1)、求证: ;(2)、若 ,求MN的长.
