河北省邢台市桥西区2021年中考数学一模试卷

试卷更新日期：2021-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，几何体圆锥的面数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 若①a+b=0，②mn=1，则下列表述正确的是（）

A、a和b ， m和n均互为相反数 B、a和b ， m和n均互为倒数 C、a和b互为倒数；m和n互为相反数 D、a和b互为相反数；m和n互为倒数

查看试题解析
3. 如图，在菱形 $A B C D$ 中，标出了四条线段的长度，其中有一个长度是标错的，这个长度是（）

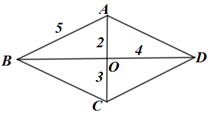A、2 B、3 C、4 D、5

查看试题解析
4. 如图所示的几何体由六块相同的小正方体搭成，若移走一块小正方体几何体的左视图发生了改变，则移走的小正方体是（）

A、① B、② C、③ D、④

查看试题解析
5. 一张正方形纸片按图1，图2对折后，再按图3打出一个半圆形小孔，则展开铺平后的图案是（）

A、 B、 C、 D、

查看试题解析

6. 育种小组对某品种小麦发芽情况进行测试，在测试基本情况相同的条件下，得到如下数据：

抽查小麦粒数	100	500	1000	2000	3000	4000
发芽粒数	95	486	968	1940	2907	$a$

则a的值最有可能是（）

A、3680 B、3720 C、3880 D、3960

查看试题解析

7. 已知每毫升血液中约有420万个红细胞，则 $5 \times 10^{2}$ 毫升血液中红细胞的个数用科学记数法表示为（）

A、 $21 \times 10^{12}$ B、 $2.1 \times 10^{13}$ C、 $21 \times 10^{8}$ D、 $2.1 \times 10^{9}$

查看试题解析
8. 嘉淇在用直尺和圆规作一个角等于已知角的步骤如下：
已知：∠AOB ．

求作：∠A'O'B'，使∠A'O'B'=∠AOB ．

作法：

⑴如图，以点O为圆心，m为半径画弧，分别交OA ， OB于点C ， D；

⑵画一条射线O'A'，以点O'为圆心，n为半径画弧，交O'A'于点C'；

⑶以点C'为圆心，p为半径画弧，与第（2）步中所画的弧相交于点D'；

⑷过点D'画射线O'B'，则∠A'O'B'=∠AOB ．

下列说法正确的是（）

A、m－p>0 B、1－p>0 C、p= $\frac{1}{2}$ n>0 D、m=n>0

查看试题解析
9. 一辆快车和一辆慢车同时从甲地出发，沿同一路线到乙地，已知快车的速度是慢车速度的1.2倍，且快车比慢车先到 $\frac{1}{4} h$ ，设慢车的速度为 $x km / h$ ，若这一路线长为 $450km$ ，那么下面所列方程正确的是（）

A、 $\frac{450}{x} = \frac{450}{x + \frac{1}{4}} + 1.2$ B、 $\frac{450}{1.2 x} = \frac{450}{x} - \frac{1}{4}$ C、 $\frac{450}{x} = \frac{450}{x + \frac{1}{4}} \times 1.2$ D、 $\frac{450}{1.2 x} = \frac{450}{x} + \frac{1}{4}$

查看试题解析
10. 已知：在 $△ A B C$ 中， $A B = A C$
求证： $∠ B = ∠ C$

证明：如图，作______

在 $△ A B D$ 和 $△ A C D$ 中，

$∵ {\begin{array}{l} A B = A C \\ ∠ B A D = ∠ C A D \\ A D = A D \end{array}$

$∴ △ A B D ≌ △ A C D$

$∴ ∠ B = ∠ C$

其中，横线应补充的条件是（）

A、 $B C$ 边上高 $A D$ B、 $B C$ 边上中线 $A D$ C、 $∠ A$ 的平分线 $A D$ D、 $B C$ 边的垂直平分线

查看试题解析
11. 若一元二次方程 $2 x^{2} - m x + 1 = 0$ 有两个不相等的实数根，则m的值可以是（）

A、3 B、2 C、1 D、0

查看试题解析
12. 如图，有三个小海岛A、B、C，其中海岛C到海岛A的距离为100海里，海岛B在海岛A北偏东70°的方向上，若海岛C在海岛B北偏西20°的方向上，且到海岛B的距离是50海里，则海岛C在海岛A（）

A、北偏东20°方向 B、北偏东30°方向 C、北偏东40°方向 D、北偏西30°方向

查看试题解析
13. 在计算 $\frac{m^{2}}{m + 1} \div \frac{\otimes}{m + 1}$ 时，把运算符号“÷”看成了“+”，得到的计算结果是m，则这道题的正确的结果是（）

A、m B、 $\frac{1}{m}$ C、 $m - 1$ D、 $\frac{1}{m - 1}$

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中， $∠ B = 60 °$ ， $A E$ 平分 $∠ B A D$ 交 $B C$ 于点E，若 $∠ A E D = 80 °$ ，则 $∠ E A C$ 的度数是（）

A、10° B、15° C、20° D、25°

查看试题解析
15. 有一题目：点P、Q、M分别表示数-1、1、5，三点在数轴上同时开始运动，点P运动方向是向左，运动速度是 $2 / s$ ；点Q、M的运动方向是向右，运动速度分别 $1 / s$ 、 $3 / s$ ，如图，在运动过程中，甲、乙两位同学提出不同的看法，甲： $3 P M - 5 P Q$ 的值不变；乙： $5 Q M - 3 P Q$ 的值不变；下列选项中，正确的是（）

A、甲、乙均正确 B、甲正确、乙错误 C、甲错误、乙正确 D、甲、乙均错误

查看试题解析
16. 如图，在△ABC中，∠BAC=90°，AB=AC ， AM是△ABC中线，D是BC边上一点(点D不与点B、C重合)，连接AD ，作AF⊥AD于点A ，且FA=DA ，连接BF交AM于点E ，设BD=x ， ME=y ，则y与x的大致图像是（）

A、 B、 C、 D、

查看试题解析

二、填空题

17. 计算： $\sqrt{18} - \sqrt{2}$ = ．

查看试题解析
18. 如图，在平面直角坐标系中，点 $A (3 ， 4)$ ，点 $B (0 ， a)$ ，点 $C (6 ， a)$ ，连接 $B C$ ，过A点作双曲线 $y = \frac{m}{x} (x > 0)$ 交线段 $B C$ 于点D（不与点B、C重合），已知 $a > 0$ ．

(1)、 $m =$ ．

(2)、若 $B D > D C$ ，则a的取值范围是．

查看试题解析
19. 如图，正六边形 $A B C D E F$ 的边长为2，M点是四边形 $C D E F$ 内的一个动点，若 $∠ C F M = ∠ M C D$ ．

(1)、 $∠ F M C =$ ；

(2)、动点M所经过的路线长是．

查看试题解析

三、解答题

20. 如图所示，某数学活动小组编制了一道有理数混合运算题，即输人一个有理数，按照自左向右的顺序运算，可得计算结果：其中“●”表示一个有理数．

(1)、已知●表示3，
①若输入数-5，求计算结果；

②若计算结果为8，求输入的数是几？

(2)、若●表示非负数，且计算结果为0，求输入数的最大值．

查看试题解析
21. 如图，约定：上方相邻两整式之和等于这两个整式下方箭头共同指向的整式．

(1)、求整式M；

(2)、请将整式N分解因式；

(3)、若 $P = - 4$ ，求x的值．

查看试题解析
22. 为迎接建党一百周年，甲、乙两名同学进行了六次党史知识测试，部分成绩如图所示，已知甲、乙两名同学六次成绩的平均数相等．

(1)、计算甲同学成绩的平均数，并补充完整乙同学成绩的折线统计图；

(2)、若乙同学成绩的方差为 $S_{乙}^{2} = 33.3$ ，请计算甲同学成绩的方差，并比较哪个同学的成绩较稳定；

(3)、甲同学成绩的中位数和众数分别记作a，b，乙同学成绩的众数记作c，在数a，b，c中随机抽取两个数，求抽到的两个数恰好相等的概率．

查看试题解析
23. 如图，点D是△ABC边BC上一点(不与点B、点C重合)，延长BC到E ，使CE=BD ，点F是直线BC外一点，且EF//AC ， DF//AB．

(1)、求证：△ABC≌OFDE；

(2)、已知∠ABC=45°，∠E=60°，连接AD．
①若点O是△ABD的外心，求∠BOD的取值范围；

②若BC= $\sqrt{3}$ +3，求AD的最小值．

查看试题解析
24. 某农业合作社计划投资200万元，开展甲、乙两项种植项目。已知两个项目的收益（万元）均与投资金额（万元）成正比例，但比例系数不同，设投资甲项目的资金为x（万元），两个项目的总收益为y（万元），且在经营过程中，获得的部分数据如下：

x（万元）

10

120

y（万元）

79

68

(1)、求y与x的函数关系式；

(2)、嘉淇说：“两个项目的总收益可以是50万元”，你同意他的说法吗？说明你的理由；

(3)、若投资甲项目的收益不低于投资乙项目的收益的 $\frac{1}{4}$ ，求y的最大值．

查看试题解析
25. 如图，在矩形ABCD中，AB=6，AD=8，点O在对角线BD上(不与点B、D重合)，以O为圆心，QB为半径作圆O交BD于点E．

(1)、sin∠ABD；

(2)、若圆O经过点A ，求圆O的面积；

(3)、若圆O与ΔACD的边所在直线相切，求OB的长．

查看试题解析
26. 我们规定：在平面直角坐标系中，横坐标、纵坐标均为整数的点，称为整点．抛物线 $y = a x^{2} + 4 a x + 4 a$ 的顶点为A，与y轴交于B点．

(1)、求点A的坐标；

(2)、若 $∠ B A O = 45 °$ ，求a的值；

(3)、已知 $a < 0$ ，点 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ 在抛物线上，当 $h - 1 \leq x_{1} \leq h + 1$ ， $x_{2} \geq 1$ 时，均满足 $y_{1} \geq y_{2}$ ，求h的取值范围；

(4)、已知 $a > 0$ ，若抛物线上A、B之间的部分与线段 $A B$ 所围成的区域内（不包括边界）没有整点，求a的值或取值范围．

查看试题解析

x（万元）	10	120
y（万元）	79	68