湖北省孝感市云梦县2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 在二次根式 $\sqrt{x - 2}$ 中，字母x的取值范围是（）

A、 $x > 2$ B、 $x < 2$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
2. 一组数据2，3，5，4，4的众数、中位数分别是（）

A、4，5 B、4，4 C、5，4 D、5，5

查看试题解析
3. 下列四组线段中，能构成直角三角形的是（）

A、4，5，6 B、6，9，10 C、5，12，14 D、7，24，25

查看试题解析
4. 计算 $(3 + \sqrt{2}) (3 - \sqrt{2})$ 的结果是（）

A、1 B、 $2 \sqrt{2}$ C、7 D、 $- 2 \sqrt{2}$

查看试题解析
5. 如图，在菱形ABCD中， $∠ B C D = 60 °$ ， $B D = 8$ ，则AB的长是（）

A、6 B、8 C、10 D、12

查看试题解析
6. 一组数据5，5，7，9，9的方差是（）

A、 $\frac{4}{7}$ B、 $\frac{8}{7}$ C、 $\frac{15}{7}$ D、 $\frac{16}{5}$

查看试题解析
7. 一次函数y=kx+b中，y随x的增大而减小，b＜0，则这个函数的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 如图，在 $R t △ A B C$ ， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ，D，E，F分别是AB，AC，AD的中点， $B C = 3$ ，则EF的长度为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{3}{2}$ D、 $\sqrt{3}$

查看试题解析
9. 如图，在矩形ABCD中，E是AB的中点，将 $△ B C E$ 沿CE翻折得到 $△ F C E$ ，连接AF，若 $∠ B C F = 30 °$ ，则 $∠ A F E$ 的度数是（）

A、 $45 °$ B、 $60 °$ C、 $75 °$ D、 $90 °$

查看试题解析
10. 一个有进水管和出水管的容器，从某时刻开始4min内只进不出水，在随后的8min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（单位：L）与时间x（单位：min）之间的关系如图所示.下列结论：
①当 $0 \leq x \leq 4$ ，y与x的函数解析式为 $y = 5 x$ .

②8min，容器内的水量为25L.

③该容器每分钟进水5L.

④该容器每分钟出水1.25L

其中正确结论的个数是（   ）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 化简 $\sqrt{\frac{9}{25}} =$ .

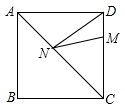
查看试题解析
12. 甲、乙两人各进行10次射击比赛，平均成绩均为9环，方差分别是：S_甲²＝2，S_乙²＝4，则射击成绩较稳定的是（选填“甲”或“乙”）．

查看试题解析
13. 直线 $y = 2 x - 5$ 与x轴交点的坐标是.

查看试题解析
14. 我国古代数学善作《九章算术》中有这样一个问题：“分有池方一文，葭生其中央，出水一尺.引葭赴岸，适与岸齐，闻水深、度长各几何.”译文：“有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面.水的深度和这根芦苇的长分别是多少？”这根芦苇的长度为尺.

查看试题解析
15. 如图，正方形ABCD的边长为4，点M在DC上，且 $D M = 1$ ，N是AC上的一点，则 $D N + M N$ 的最小值为.

查看试题解析
16. 如图，直线 $y_{1} = k x + b$ 过点A(0，2)，且与直线 $y_{2} = m x$ 交于点P(1，m)，则不等式组 $m x$ > $k x + b$ > $m x$ -2的解集是


查看试题解析

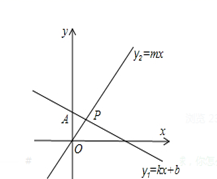
三、解答题

17. 计算： $\sqrt{27} \div \sqrt{3} - 2 \sqrt{12} \times \frac{\sqrt{3}}{4}$

查看试题解析
18. 如图，在 $▱$ ABCD中，点E，F分别在BC，AD上，且BE=FD，求证：四边形AECF是平行四边形．

查看试题解析
19. 如图，在边长为1的小正方形组成的网格中， $△ A B C$ 的三个顶点都在格点上，请按要求完成下列各题.

(1)、在网格中找到一个格点D，使A、B、C、D四个点构成的四边形是平行四边形，画出此平行四边形；

(2)、通过计算，判断 $△ A B C$ 的形状.

查看试题解析
20. 国家规定“中小学生每天在校体育活动时间不低于1h”.为此，某市就“每天在校体育活动时间”的问题随机调查了辖区360名初中学生.根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：
A组： $t < 0.5 h$ B组： $0.5 h \leq t < 1 h$ C组： $1 h \leq t < 1.5 h$ D组： $t \geq 1.5 h$

请根据上述信息解答下列问题：

(1)、求出C组的人数，补全条形统计图；

(2)、本次调查数据的中位数落在组内；

(3)、若该辖区内约有27000名初中生，请你估计其中达到国家规定体育活动时间的人数约有多少？

查看试题解析
21. 已知：如图，平行四边形ABCD中，O是CD的中点，连接AO并延长，交BC的延长线于点E.

(1)、求证： $△ A O D ≌ △ E O C$ ；

(2)、连接AC，DE，当 $∠ B = ∠ A E B =$ °，四边形ACED是正方形？请说明理由.

查看试题解析
22. 某“水上世界”夏季门票销售分为两类，一类为散客门票，价格为30元/张；另一类为团体门票（一次性购买门票10张及以上），每张门票价格在散客门票价格基础上打8折.某班部分同学要去该“水上世界”游玩，设参加游玩人数为x人，购买门票需要y元.

(1)、如果每人分别买票，求y与x之间的函数解析式；

(2)、如果买团体票，求y与x之间的函数解析式，并写出自变量的取值范围；

(3)、若该班恰好有9人参加游玩，按哪类方式购票比较省钱？请你根据参加游玩人数变化设计一种比较省钱的购票方案

查看试题解析
23. 如图1，在正方形ABCD中，点M、N分别在边BC、CD上，AM、AN分别交BD于点P、Q，连接CQ、MQ.且 $C Q = M Q$ .

图1 图2

(1)、求证： $∠ Q A B = ∠ Q M C$

(2)、求证： $∠ A Q M = 90 °$

(3)、如图2，连接MN，当 $B M = 2$ ， $C N = 3$ ，求 $△ A M N$ 的面积

查看试题解析
24. 如图1，在平面直角坐标系中，直线 $y = - \frac{2}{3} x + b$ 分别与x轴、y轴交于A、B，且点A坐标为 $(6 ， 0)$ ，点C为AB的中点.

(1)、直接写出点C的坐标；

(2)、点P为直线AB上的一个动点，过点P作x轴的垂线，与直线OC交于点Q，设点P的横坐标为m，线段PQ的长度为d，求d与m的函数解析式（写出自变量的取值范围）；

(3)、如图2，当点P在线段AB上，在第一象限内有一点N，使得四边形OPNB为菱形，求出点N点坐标.

查看试题解析