湖北省襄阳市襄州区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-05-24 类型:期末考试
一、单选题
-
1. 下列各式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列各组数据中,不能作为直角三角形的三边长是( )A、3,4,6 B、5,5, C、5,12,13 D、6,8,104. 一次函数y=3x﹣6的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 已知正比例函数 的图象上两点 、 ,且 ,下列说法正确的是A、 B、 C、 D、不能确定6. 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
 A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形7. 学校准备从甲、乙、丙、丁四名同学中选一名代表学校参加襄阳市七巧科技创新大赛,这四名同学平时成绩的平均数及方差如下表所示:
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形7. 学校准备从甲、乙、丙、丁四名同学中选一名代表学校参加襄阳市七巧科技创新大赛,这四名同学平时成绩的平均数及方差如下表所示:甲
乙
丙
丁
平均数
8.5
9
9
8
方差
1
1.2
0.8
1.8
如果要选出一个成绩较好且状态稳定的同学去参赛,那么应该选择( )
A、甲 B、乙 C、丙 D、丁8. 某地招录教师要进行笔试和面试,其中笔试占 ,面试占 .莫小贝也参与了这次教师招录考试,她的笔试成绩90分,面试成绩85分,那么莫小贝的最后成绩是( )A、86分 B、87分 C、87.5分 D、88分9. 若一次函数 ( 为常数,且 )的图象经过点 , ,则不等式 的解为( )A、 B、 C、 D、10. 如图,四边形 为菱形,点A的坐标为 ,点C的坐标为 ,点D在y轴上,则点B的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若式子 在实数范围内有意义,则x的取值范围是.12. 如图一根竹子长为8米,折断后竹子顶端落在离竹子底端4米处,折断处离地面高度是米.
 13. 一组数据3,2,7,a,7的平均数是5,则这组数据的方差是.14. 已知一次函数 ,当 时,函数 的最大值是 .15. 如图,正方形 中,E为 中点, , , 交 于P,则 的度数为.
13. 一组数据3,2,7,a,7的平均数是5,则这组数据的方差是.14. 已知一次函数 ,当 时,函数 的最大值是 .15. 如图,正方形 中,E为 中点, , , 交 于P,则 的度数为. 16. 如图,在矩形 中,点E为边 上一点,连接 ,作 的平分线,交 于点F,连接 ,若 , ,且 ,则 .
16. 如图,在矩形 中,点E为边 上一点,连接 ,作 的平分线,交 于点F,连接 ,若 , ,且 ,则 .
三、解答题
-
17. 计算下列各题:(1)、 ;(2)、 .18. 如图,四边形 是菱形, 于 , 交 的延长线于 ,求证: .
 19. 小锤和豆花要测量校园里的一块四边形场地ABCD(如图所示)的周长,其中边BC上有水池及建筑遮挡,没有办法直接测量其长度.小锤经测量得知AB=AD=5m,∠A=60°,DC=13m,∠ABC=150°.豆花说根据小锤所得的数据可以求出CB的长度.你同意豆花的说法吗?若同意,请求出CB的长度;若不同意,请说明理由.
19. 小锤和豆花要测量校园里的一块四边形场地ABCD(如图所示)的周长,其中边BC上有水池及建筑遮挡,没有办法直接测量其长度.小锤经测量得知AB=AD=5m,∠A=60°,DC=13m,∠ABC=150°.豆花说根据小锤所得的数据可以求出CB的长度.你同意豆花的说法吗?若同意,请求出CB的长度;若不同意,请说明理由. 20. 2020年4月是我国第32个爱国卫生月.某校八年级通过网课举行了主题为“防疫有我,爱卫同行”的知识竞赛活动,对全校2200名学生“预防新冠病毒知识”进行了测试(试卷满分100分),从中随机抽取了20名学生的测试卷,按 五个级别分别进行了统计,其中得分在C级别这一范围内的成绩分别是:70,72,74,76,77,78,78,78,79,79
20. 2020年4月是我国第32个爱国卫生月.某校八年级通过网课举行了主题为“防疫有我,爱卫同行”的知识竞赛活动,对全校2200名学生“预防新冠病毒知识”进行了测试(试卷满分100分),从中随机抽取了20名学生的测试卷,按 五个级别分别进行了统计,其中得分在C级别这一范围内的成绩分别是:70,72,74,76,77,78,78,78,79,79(数据整理与描述)将调查结果绘制成如下的统计表和不完整的统计图:

级别
分数
频数
频率
A
2
0.10
B
m
0.20
C
10
0.50
D
3
n
E
1
0.05
(数据应用)请根据以上信息解答下列问题:
(1)、填空: , ;(2)、补全频数分布直方图;(3)、被抽取的20名学生成绩的中位数为;(4)、若这次测试成绩不低于80分的确定为优秀,请估计该校这次测试获得优秀的学生人数.21. 将折叠书架画出侧面示意图, 为面板架, 为支撑架, 为锁定杆,F可在 上移动或固定.已知 .如图甲,将面板 竖直固定时( ),点F恰为 的中点.如图乙,当 时, .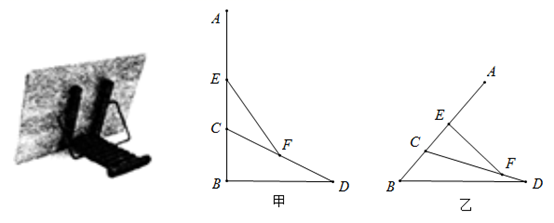 (1)、求锁定杆 的长度;(2)、求支撑架 的长度.22. 已知一次函数 的图象经过点 且与正比例函数 的图象相交于点 ,求:
(1)、求锁定杆 的长度;(2)、求支撑架 的长度.22. 已知一次函数 的图象经过点 且与正比例函数 的图象相交于点 ,求: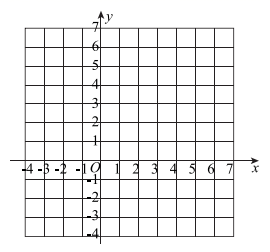 (1)、a的值;(2)、求一次函数 的表达式;(3)、请你画出这两个函数的图象,并判断当 取何值时, ;(4)、求这两个函数图象与 轴围成的三角形的面积.23. 如图,在 中, , , ,点E从点A出发沿 以每秒 的速度向点B运动,同时点D从点C出发沿 以每秒 的速度向点A运动,运动时间为t秒( ),过点D作 于点F.
(1)、a的值;(2)、求一次函数 的表达式;(3)、请你画出这两个函数的图象,并判断当 取何值时, ;(4)、求这两个函数图象与 轴围成的三角形的面积.23. 如图,在 中, , , ,点E从点A出发沿 以每秒 的速度向点B运动,同时点D从点C出发沿 以每秒 的速度向点A运动,运动时间为t秒( ),过点D作 于点F. (1)、试用含t的式子表示 、 、 的长;(2)、如图①,连接 ,求证四边形 是平行四边形;(3)、如图②,连接 ,当t为何值时,四边形 是矩形?并说明理由.24. 某大药房采购员要到厂家批发购买A、B型手持红外测温仪共100个.大药房采购员看到某人两次购买(均按批发价)情况及药房的零售价如下表:
(1)、试用含t的式子表示 、 、 的长;(2)、如图①,连接 ,求证四边形 是平行四边形;(3)、如图②,连接 ,当t为何值时,四边形 是矩形?并说明理由.24. 某大药房采购员要到厂家批发购买A、B型手持红外测温仪共100个.大药房采购员看到某人两次购买(均按批发价)情况及药房的零售价如下表: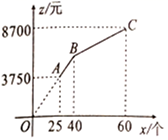
第一次
第二次
药房零售价
A型测温仪
1(个)
3(个)
B型测温仪
3(个)
2(个)
120(元)
进货款
420(元)
560(元)
(1)、求每个A型测温仪、B型测温仪的进货价;(2)、设购买A型测温仪x个,当 时,大药房按零售价销售(O、A、B三点共线);当 时,大药房打折销售A型测温仪,打折前、后销售A型测温仪的总收入z(元)与x(个)之间的关系如图所示(若需要使用z,可直接写出z的函数解析式),假设100个A、B型测温仪全部售完,大药房总获利润为y元;①求y与x之间的函数解析式;
②求该大药房购进A、B型测温仪各多少个时,才能使获得的总利润最大?最大利润为多少元?
25. 如图正方形 , 与 相交于点O(O不与D、E重合). (1)、如图(1),当 ,
(1)、如图(1),当 ,①求证: ;
②求证: ;
(2)、如图(2),当 ,边长 , ,求 的长.