湖北省襄阳市襄城区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子为最简二次根式的是（　　）

A、 $\sqrt{a^{2} + b^{2}}$ B、 $\sqrt{a^{2}}$ C、 $\sqrt{12 a}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
2. 使 $\sqrt{x - 3}$ 有意义的x的取值范围是（）

A、x≤3 B、x＜3 C、x≥3 D、x＞3

查看试题解析
3. △ABC满足下列条件中的一个，其中不能说明△ABC是直角三角形的是（）

A、b²＝（a＋c）（a﹣c） B、a∶b∶c＝1∶ $\sqrt{3}$ ∶2 C、∠C＝∠A﹣∠B D、∠A∶∠B∶∠C＝3∶4∶5

查看试题解析
4. 如图，有一个水池，水池的横截面是一边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺.如果把这根芦苇拉向水池的一边，它的顶端恰好到达池边的水面，这根芦苇的长度为（　　）尺.

A、10 B、12 C、13 D、14

查看试题解析
5. 矩形、菱形、正方形的对角线都具有的性质是（）

A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、对角线互相垂直平分

查看试题解析
6. 如图是甲、乙两人追赶过程中路程和时间函数关系的图象，下列关于图象的叙述正确的个数是（）
（1）甲追乙；（2）甲的速度是4km/h；（3）乙出发5h与甲相遇；（4）乙共走20km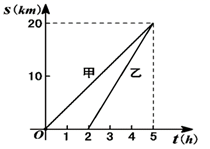

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，直线y＝kx+6经过点（3，0），则关于x的不等式kx+6＜0的解集是（　　）

A、x＞3 B、x＜3 C、x＞6 D、x＜6

查看试题解析
8. 关于数据3， $- 2$ ， $- 1$ ，0，5的说法正确的是（）

A、平均数为 $- 1$ B、中位数为1 C、众数为5 D、方差为6.8

查看试题解析
9. 如图，在 $△ A B C$ 中，D，E分别是 $A B$ ， $A C$ 的中点，则下列说法正确的是（）

A、 $A E = B D$ B、 $B D = D E$ C、 $∠ D E C + ∠ B = 180 °$ D、 $∠ B D E + ∠ B = 180 °$

查看试题解析
10. 如图，正方形ABCD的边长为8，在各边上顺次截取AE=BF=CG=DH=5，则四边形EFGH的面积是（）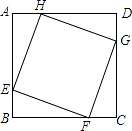

A、30 B、34 C、36 D、40

查看试题解析

二、填空题

11. 甲、乙两位同学在6次线上数学考试中，成绩的平均数都是105分，方差分别是S_甲²＝1.2，S_乙²＝2.5，则同学的成绩更稳定.

查看试题解析
12. 直线y＝ $\frac{1}{2}$ x+3与两坐标轴围成的三角形的面积为.

查看试题解析
13. 如图，在▱ABCD中，对角线AC、BD相交于点O，在不添加任何辅助线的情况下，请你添加一个条件，使▱ABCD是菱形.

查看试题解析
14. 如图所示的网格是正方形网格，则 $∠ A B C + ∠ A C B =$ °（点A，B，C是网格线交点）.

查看试题解析
15. 若x＝ $\sqrt{3}$ ＋1，y＝ $\sqrt{3}$ ﹣1，则（x＋y）²＝.

查看试题解析
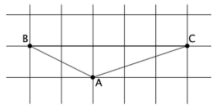16. 如图，在矩形ABCD中，∠B的平分线BE与AD交于点E，∠BED的平分线EF与DC交于点F，当点F是CD的中点时，若AB＝4，则BC＝.

查看试题解析

三、解答题

17. 计算：（ $\sqrt{2}$ +1）²﹣ $\sqrt{18}$ +2 $\sqrt{\frac{1}{2}}$ ．

查看试题解析
18. 如图，在△ABC中，CD⊥AB于点D，AC＝20，CD＝12，BD＝9.

(1)、求BC的长.

(2)、求△ABC的面积.

查看试题解析

19. 为普及防治新型冠状病毒感染的科学知识和有效方法，不断增强同学们的自我保护意识，学校举办了新型冠状病毒疫情防控网络知识竞答活动，试卷题目共10题，每题10分.现分别从七年级的三个班中各随机取10名同学的成绩（单位：分），收集数据如表：

1班：90，70，80，80，80，80，80，90，80，100；

2班：70，80，80，80，60，90，90，90，100，90；

3班：90，60，70，80，80，80，80，90，100，100.

整理数据：

分数人数班级	60	70	80	90	100
1班	0	1	6	2	1
2班	1	1	3	a	1
3班	1	1	4	2	2

分析数据：

	平均数	中位数	众数
1班	83	80	80
2班	83	c	d
3班	b	80	80

根据以上信息回答下列问题：

(1)、请直接写出表格中a，b，c，d的值；

(2)、比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由；

(3)、为了让同学们重视疫情防控知识的学习，学校将给竞答成绩满分的同学颁发奖状，该校七年级新生共600人，试估计需要准备多少张奖状？

查看试题解析

20. 如图，在 $△ A B C$ 中，∠BAC＝90°，DE是 $△ A B C$ 的中位线，AF是 $△ A B C$ 的中线.求证DE＝AF.

证法1：∵DE是 $△ A B C$ 的中位线，

∴DE＝ ▲ .

∵AF是 $△ A B C$ 的中线，∠BAC＝90°，

∴AF＝ ▲ ，

∴DE＝AF.

请把证法1补充完整，连接EF，DF，试用不同的方法证明DE＝AF

证法2：

查看试题解析
21. 已知y与x＋2成正比例，且当x＝1时，y＝6；

(1)、求出y与x之间的函数关系式；

(2)、当x＝﹣3时，求y的值.

查看试题解析
22. 如图，在矩形ABCD中，E是AD上一点，PQ垂直平分BE，分别交AD、BE、BC于点P、O、Q，连接BP、EQ.

(1)、求证：四边形BPEQ是菱形；

(2)、若AB=6，BE=10，求PQ的长.

查看试题解析
23. 河南灵宝苹果为中华苹果之翘楚，被誉为“中华名果”.某水果超市计划从灵宝购进“红富士”与“新红星”两种品种的苹果.已知2箱红富士苹果的进价与3箱新红星苹果的进价的和为282元，且每箱红富士苹果的进价比每箱新红星苹果的进价贵6元.

(1)、求每箱红富士苹果的进价与每箱新红星苹果的进价分别是多少元？

(2)、如果购进红富士苹果有优惠，优惠方案是：购进红富士苹果超过20箱，超出部分可以享受七折优惠.若购进 $a$ （ $a > 0$ ，且 $a$ 为整数）箱红富士苹果需要花费 $w$ 元，求 $w$ 与 $a$ 之间的函数关系式；

(3)、在（2）的条件下，超市决定在红富士、新红星两种苹果中选购其中一种，且数量超过20箱，请你帮助超市选择购进哪种苹果更省钱.

查看试题解析
24. 如图，已知正方形ABCD，点E在BC上，点F在CD延长线上，BE＝DF

(1)、求证：AE＝AF；

(2)、若BD与EF交于点M，连接AM，试判断AM与EF的数量与位置关系，并说明理由.

查看试题解析