湖北省襄阳市老河口市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-05-24 类型:期末考试
一、单选题
-
1. 二次根式 中,字母a的取值范围是( )
A、a<1 B、a≤1 C、a≥1 D、a>12. 等边三角形的边长为4,则该三角形的面积为( )A、 B、 C、 D、33. 在平行四边形ABCD中,∠B=60°,那么下列各式中,不能成立的是( )A、∠D=60° B、∠A=120° C、∠B+∠D=120° D、∠C+∠A=120°4. 从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前的速度随时间的增加而逐渐增大,这个问题中自变量是( )A、物体 B、速度 C、时间 D、空气5. 已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( ) A、x<0 B、-1<x<1或x>3 C、x>-1 D、x<-1或1<x<36. 一次函数y=kx-k(k<0)的图象大致是( )A、
A、x<0 B、-1<x<1或x>3 C、x>-1 D、x<-1或1<x<36. 一次函数y=kx-k(k<0)的图象大致是( )A、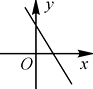 B、
B、 C、
C、 D、
D、 7. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如表:
7. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如表:投中次数
3
5
6
7
8
人数
1
3
2
2
2
则这些队员投中次数的众数、中位数和平均数分别为( )
A、5,6,6 B、2,6,6 C、5,5,6 D、5,6,58. 已知一组数据为7,1,5,x,8,它们的平均数是5,则这组数据的方差为( )A、3 B、4.6 C、5.2 D、69. 若正比例函数y=(2-3m)x的图象经过点A(x1 , y1)和B(x2 , y2),且当x1<x2时,y1>y2 , 则m的取值范围是( )A、m>0 B、m> C、m< D、m<010. 如图,在菱形ABCD中,E,F分别是BC和CD的中点,且AE⊥BC,AF⊥CD,若AE= ,则菱形ABCD的周长等于( ) A、 B、 C、4 D、8
A、 B、 C、4 D、8二、填空题
-
11. 计算: .12. 在 中,AB=20,BC=16,AC=12,点D为AB边中点,则CD的长为.13. 一组数据2,4,8,5,4的中位数是a,则a的值是.14. 某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为92分、85分、90分,综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为分.15. 若一次函数y=x+2的图象与x轴的交点坐标为 .16. 若直线y= x+a和直线y=x+b的交点坐标为(m,8),则a+b= .17. 某书定价40元,如果一次购买20本以上,超过20本的部分打八折.试写出付款金额y(单位:元)与购书数量x(单位:本)之间的函数关系.18. 如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交BC、AD于点E、F,若BE=3,AF=5,则AC的长为.

三、解答题
-
19. 计算: .20. 如图,在 中,AB=25,BC=30,BC边上的中线AD=20,求AC.
 21. 在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E、F为垂足,求证:四边形AFCE是平行四边形.
21. 在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E、F为垂足,求证:四边形AFCE是平行四边形. 22. 已知一次函数的图象经过点(9,0)和点(24,20),求这个函数的解析式.23. 如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD,OE交CD于点F.求证:AD=2EF.
22. 已知一次函数的图象经过点(9,0)和点(24,20),求这个函数的解析式.23. 如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD,OE交CD于点F.求证:AD=2EF. 24. 随机抽取某小吃店一周的营业额(单位:元)如下表:
24. 随机抽取某小吃店一周的营业额(单位:元)如下表:星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
540
680
640
640
780
1110
1070
5460
(1)、分析数据,填空:这组数据的平均数是元,中位数是元,众数是元.(2)、估计一个月的营业额(按30天计算):①星期一到星期五营业额相差不大,用这5天的平均数估算合适吗?为什么?
②选择一个你认为最合适的数据估算这个小吃店一个月的营业额.
25. 1号探测气球从海拔5米处出发,以1 米/分的速度上升.与此同时,2号探测气球从海拔15米处出发,以0.5米/分的速度上升,两个气球都上升了1小时.1号、2号气球所在位置的海拔分别为y1 , y2(单位:米),上升的时间为x(单位:分).(1)、请分别写出y1 , y2与x的函数关系式;(2)、在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?(3)、至少上升多长时间,两个气球的海拔相差不少于15米?

