湖北省武汉市硚口区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-05-24 类型:期末考试
一、单选题
-
1. 式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 五名女生的体重(单位:kg)分别为:37、40、38、42、42,这组数据的众数和中位数分别是( )A、2、40 B、42、38 C、40、42 D、42、404. 下列边长的三角形不是直角三角形的是( )A、 B、 C、 D、5. 下列命题正确的是( )A、有一个角是直角的平行四边形是矩形 B、四条边相等的四边形是矩形 C、有一组邻边相等的平行四边形是矩形 D、对角线相等的四边形是矩形6. “漏壶”是一种这个古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是( )
 A、
A、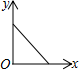 B、
B、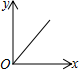 C、
C、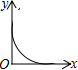 D、
D、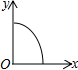 7. 将直线 向上平移2个单位长度后,所得的直线的解析式为( )A、 B、 C、 D、8. 顺次连接四边形 的四边中点所得的四边形是正方形,则下列判断正确的是( )A、四边形 一定是正方形 B、四边形 一定是菱形 C、四边形 一定是矩形 D、四边形 的对角线一定相互垂直且相等9. 甲、乙两车从A城出发前往B城,在整个行程中,甲、乙两车离开A城的距离y与时刻t的对应关系如图所示,则下列结论:① 两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③甲车的平均速度比乙车的平均速度每小时慢40千米;④当甲、乙两车相距20千米时, 7或8.其中正确的结论个数为( )
7. 将直线 向上平移2个单位长度后,所得的直线的解析式为( )A、 B、 C、 D、8. 顺次连接四边形 的四边中点所得的四边形是正方形,则下列判断正确的是( )A、四边形 一定是正方形 B、四边形 一定是菱形 C、四边形 一定是矩形 D、四边形 的对角线一定相互垂直且相等9. 甲、乙两车从A城出发前往B城,在整个行程中,甲、乙两车离开A城的距离y与时刻t的对应关系如图所示,则下列结论:① 两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③甲车的平均速度比乙车的平均速度每小时慢40千米;④当甲、乙两车相距20千米时, 7或8.其中正确的结论个数为( ) A、1个 B、2个 C、3个 D、4个10. 如图,平面直角坐标系 中,点 的坐标为 , 轴,垂足为 ,点 从原点 出发向 轴正方向运动,同时,点 从点 出发向点 运动,当点 到达点 时,点 、 同时停止运动,若点 与点 的速度之比为 ,则下列说法正确的是( )
A、1个 B、2个 C、3个 D、4个10. 如图,平面直角坐标系 中,点 的坐标为 , 轴,垂足为 ,点 从原点 出发向 轴正方向运动,同时,点 从点 出发向点 运动,当点 到达点 时,点 、 同时停止运动,若点 与点 的速度之比为 ,则下列说法正确的是( )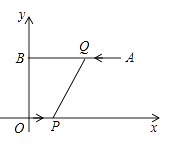 A、线段 始终经过点 B、线段 始终经过点 C、线段 始终经过点 D、线段 不可能始终经过某一定点
A、线段 始终经过点 B、线段 始终经过点 C、线段 始终经过点 D、线段 不可能始终经过某一定点二、填空题
-
11. 计算 的结果是 .12. 某公司欲招聘一名员工,对甲进行了笔试和面试,其笔试和面试的成绩分别为80分和90分,若按笔试成绩占 ,面试成绩占 计算综合成绩,则甲的综合成绩为分.13. 如图,在正方形 的外侧,作等边 ,则 的度数是 .
 14. “黄金1号”玉米种子的价格为5元 ,如果一次购买 以上的种子,超过 部分的种子的价格打8折,若购买种子数量为 ,付款金额为y元.当 时,y与x的函数解析式为;当 时y与x的函数解析为.15. 已知一次函数 和 ,当自变量 时, ,则k的取值范围为.16. 如图,动点 分别在正方形 的边 上, ,过点C作 ,垂足为G,连接 ,若 ,则线段 长的最小值为.
14. “黄金1号”玉米种子的价格为5元 ,如果一次购买 以上的种子,超过 部分的种子的价格打8折,若购买种子数量为 ,付款金额为y元.当 时,y与x的函数解析式为;当 时y与x的函数解析为.15. 已知一次函数 和 ,当自变量 时, ,则k的取值范围为.16. 如图,动点 分别在正方形 的边 上, ,过点C作 ,垂足为G,连接 ,若 ,则线段 长的最小值为.
三、解答题
-
17. 已知一次函数 的图象经过点 .(1)、若直线 与直线 平行,求这个一次函数的解析式;(2)、若直线 经过点 ,求m的值.18. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF//BD交OE的延长线于点F,连接DF.
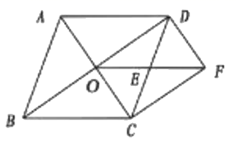
求证:
(1)、△ODE≌△FCE;(2)、四边形OCFD是矩形。19. 中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的数量最少的是5本,最多的是8本,并根据调查结果绘制了如下不完整的图表. (1)、扇形统计图中的 , ;(2)、扇形统计图中课外阅读5本的扇形的圆心角大小为;(3)、求被调查学生课外阅读的平均本数;(4)、若该校八年级共有1200名学生,请估计该校八年级学生课外阅读至少7本的人数.20. 如图是由边长为1的小正方形构成的 网格,每个小正方形的顶点叫做格点.四边形 的顶点是格点.点M是边 与网格线的交点,仅用无刻度的直尺在给定网格中按步骤完成下列画图,画图过程用虚线表示,画图结果用实线表示.
(1)、扇形统计图中的 , ;(2)、扇形统计图中课外阅读5本的扇形的圆心角大小为;(3)、求被调查学生课外阅读的平均本数;(4)、若该校八年级共有1200名学生,请估计该校八年级学生课外阅读至少7本的人数.20. 如图是由边长为1的小正方形构成的 网格,每个小正方形的顶点叫做格点.四边形 的顶点是格点.点M是边 与网格线的交点,仅用无刻度的直尺在给定网格中按步骤完成下列画图,画图过程用虚线表示,画图结果用实线表示.
( 1 )过点C画线段 ,使 ,且 ;
( 2 )在边 上画一点F,使直线 平分四边形 的面积;
( 3 )过点M画线段 ,使 ,且 .
21. 如图,直线 交x轴于点A,交y轴于点B,与直线 交于点 . (1)、求 的值;(2)、已知点 ,过点P作垂直于y轴的直线与直线 交于点M,过点P作垂直于x轴的直线与直线 交于点N(P与N不重合).若 ,求n的值.22. A城有肥料 ,B城有肥料 .现要把这些肥料全部运往 两乡,C乡需要肥料 ,D乡需要肥料 ,从A城运往 两乡的运费分别为20元 和25元 ;从B城运往 两乡的运费分别为15元 和35元 .设从B城运往D乡点的肥料为 .(1)、填表:
(1)、求 的值;(2)、已知点 ,过点P作垂直于y轴的直线与直线 交于点M,过点P作垂直于x轴的直线与直线 交于点N(P与N不重合).若 ,求n的值.22. A城有肥料 ,B城有肥料 .现要把这些肥料全部运往 两乡,C乡需要肥料 ,D乡需要肥料 ,从A城运往 两乡的运费分别为20元 和25元 ;从B城运往 两乡的运费分别为15元 和35元 .设从B城运往D乡点的肥料为 .(1)、填表:A城
B城
总计
C乡
240
D乡
260
总计( )
200
300
500
(2)、从A城运往两乡的总运费为 元,从B城运往两乡的总运费为 元.①分别写出 与 之间的函数关系式(不要求写自变量的取值范围)
②试比较 两城总运费的大小.
(3)、由于从B城到D乡的路况得到改善,缩短了运输时间运费每吨减少a元 ,其余路线运费不变,若 两城总运费和的最小值不小于10160元,求a的取值范围.

