湖北省武汉市江岸区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-05-24 类型:期末考试
一、单选题
-
1. 若代数式 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 下列各式计算正确的是( )A、 B、 C、 D、3. 已知Rt△ABC的三边分别为a、b、c,则下列结论不可能成立的是( )A、a2﹣b2=c2 B、∠A﹣∠B=∠C C、∠A:∠B:∠C=3:4:5 D、a:b:c=7:24:254. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
成绩m
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
2
3
4
1
则这些运动员成绩的众数是( )
A、1.65 B、1.75 C、1.70 D、1.605. 直线y=﹣3x+2图象不经过下列哪个象限( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 下列命题错误的是( )A、平行四边形的对角相等 B、正方形有四条对称轴 C、两条对角线相等的平行四边形是矩形 D、对角线互相垂直的四边形是菱形7. 一次函数 的图象经过点 ,当 时, 则m的取值范围是( )A、 B、 C、 D、8. 如图,正方形ABCD中,E、F分别在边CD,AD上, 于点G,若BC=4,AF=1,则CE的长为( ) A、3 B、 C、 D、9. 一个装有进水管和出水管的空容器,从某时刻开始 内只进水不出水,容器内存水 ,在随后的 内既进水又出水,容器内存水 ,接着关闭进水管直到容器内的水放完.若每分钟进水和出水量是两个常数,容器内的水量 (单位: )与时间 (单位: )之间的函数关系的图象大致的是( )A、
A、3 B、 C、 D、9. 一个装有进水管和出水管的空容器,从某时刻开始 内只进水不出水,容器内存水 ,在随后的 内既进水又出水,容器内存水 ,接着关闭进水管直到容器内的水放完.若每分钟进水和出水量是两个常数,容器内的水量 (单位: )与时间 (单位: )之间的函数关系的图象大致的是( )A、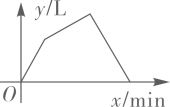 B、
B、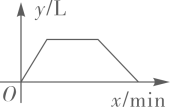 C、
C、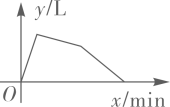 D、
D、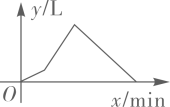 10. 一次函数 有下列结论:(1)当k=1时,图象与坐标轴围成的三角形的面积为3,则 ;(2)当b=1时,图象与函数 的图象有两个交点,则 ;下列结论正确的是( )A、(1)正确 B、(1)(2)正确 C、(2)正确 D、都不正确
10. 一次函数 有下列结论:(1)当k=1时,图象与坐标轴围成的三角形的面积为3,则 ;(2)当b=1时,图象与函数 的图象有两个交点,则 ;下列结论正确的是( )A、(1)正确 B、(1)(2)正确 C、(2)正确 D、都不正确二、填空题
-
11. 计算: .12. 点A(1,5)在一次函数y=2x+m的图象上,则m等于.13. 统计学校的排球队员的年龄,发现有12岁,13岁,14岁,15岁等四种年龄,统计结果如下:
年龄岁
12
13
14
15
个数
2
4
6
8
则根据表中信息可以判断该排球队队员的平均年龄是岁;
14. 如图,平行四边形ABCD,将四边形CDMN沿线段MN折叠,得到四边形QPMN,已知 ,则 . 15. 把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为 .
15. 把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为 .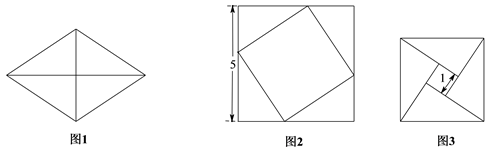 16. 在平面直角坐标系中,垂直x轴的直线l分别与函数 的图象交于P、Q两点,若平移直线l,可以使P、Q都在x轴的下方,则实数a的取值范围是.17. 计算: .
16. 在平面直角坐标系中,垂直x轴的直线l分别与函数 的图象交于P、Q两点,若平移直线l,可以使P、Q都在x轴的下方,则实数a的取值范围是.17. 计算: .三、解答题
-
18. 如图,在菱形ABCD中,对角线AC,点E,F分别在AB,AD上,BE=DF,连接EF.

求证:
19. 2019年是中华人民共和国建国70周年,武汉市某学校开展了“我和我的祖国”主题学习竞赛活动,学校3000名学生全部参加了竞赛,结果所有学生的成绩都不低于60分(满分100分),为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表,根据表中的信息,解答下列问题:成绩x(分)分组
频数
频率
15
0.30
a
0.40
10
b
5
0.10
(1)、表中 ; .(2)、判断:这组数据的众数一定落在 范围内,这个说法(填正确或错误).(3)、若成绩不小于80分为优秀,则全校大约有多少名学生获得优秀成绩?20. 如图,在平面直角坐标系中, ; (1)、求直线AB的解析式;(2)、已知 在直线AB的下方, 的面积为10,求m.21. 在10×10网格中,点A和直线l的位置如图所示;
(1)、求直线AB的解析式;(2)、已知 在直线AB的下方, 的面积为10,求m.21. 在10×10网格中,点A和直线l的位置如图所示; (1)、将点A向右平移6个单位,再向上平移2个单位得到点B,在图1中网格中标出点B,并写出线段AB的长度;(2)、在(1)中的条件下,在直线l上确定一点P,使的值最小,在图1中保留画图痕迹,并直接写出线段 的最小值:;(3)、点C为直线l上格点,是以AB为斜边的直角三角形,在图2网格中标出C,写出线段AC=;22. 为拓展学生视野,促进书本知识与生活实践的深度融合,某中学组织八年级全体学生前往东西湖研学基地开展研学活动,在此活动中一共有234名学生和6名教师,学校计划此次研学活动的租金费用不超过2300元,为安全起见,每辆客车上至少要有1名老师,现有甲、乙两种大型客车,它们的载客量和租金如表所示:
(1)、将点A向右平移6个单位,再向上平移2个单位得到点B,在图1中网格中标出点B,并写出线段AB的长度;(2)、在(1)中的条件下,在直线l上确定一点P,使的值最小,在图1中保留画图痕迹,并直接写出线段 的最小值:;(3)、点C为直线l上格点,是以AB为斜边的直角三角形,在图2网格中标出C,写出线段AC=;22. 为拓展学生视野,促进书本知识与生活实践的深度融合,某中学组织八年级全体学生前往东西湖研学基地开展研学活动,在此活动中一共有234名学生和6名教师,学校计划此次研学活动的租金费用不超过2300元,为安全起见,每辆客车上至少要有1名老师,现有甲、乙两种大型客车,它们的载客量和租金如表所示:甲型车
乙型车
载客量
45
30
租金
400
280
(1)、共需租多少辆汽车?(2)、学校共有租车方案?最少租车费是多少?23. 已知:正方形ABCD (1)、如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG//BF,交正方形外角的平分线CG于点G,连接GF.
(1)、如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG//BF,交正方形外角的平分线CG于点G,连接GF.求证:
① ;
②求证:四边形BRGF是平行四边形.
(2)、如图,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,分类说明满足PE+PF=9的点P的位置情况. 24. 平面直角坐标系中,直线 与x轴分别交于点B,A;
24. 平面直角坐标系中,直线 与x轴分别交于点B,A; (1)、直接写出直线AB关于x轴对称的直线BC的解析式;(2)、如图1,直线BC与直线y=x交于E点,点P为y轴上一点,PE=PB,求P点坐标;(3)、如图2,点P为y轴上一点, 直线EP与直线AB交于点M,求M点的坐标.
(1)、直接写出直线AB关于x轴对称的直线BC的解析式;(2)、如图1,直线BC与直线y=x交于E点,点P为y轴上一点,PE=PB,求P点坐标;(3)、如图2,点P为y轴上一点, 直线EP与直线AB交于点M,求M点的坐标.