湖北省随州市广水市2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $\sqrt{4}$ 的结果是（）

A、 $\pm 2$ B、2 C、 $- 2$ D、4

查看试题解析
2. 若二次根式 $\sqrt{3 - a}$ 有意义，则a的取值范围是（）

A、a＞3 B、a≥3 C、a≤3 D、a≠3

查看试题解析
3. 满足下列条件的 $Δ A B C$ 中，不是直角三角形的是 $($ $)$

A、 $b^{2} = c^{2} - a^{2}$ B、 $a ： b ： c = 3 ： 4 ： 5$ C、 $∠ C = ∠ A - ∠ B$ D、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$

查看试题解析
4. 若平行四边形中两个内角的度数比为1：2，则其中较小的内角是（　　）

A、60° B、90° C、120° D、45°

查看试题解析
5. 如图，下列四组条件中.不能判定四边形ABCD是平行四边形的是（　　）

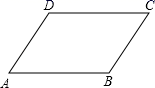A、AB＝DC，AD＝BC B、AB∥DC，AD∥BC C、AB∥DC，AD＝BC D、AB∥DC，AB＝DC

查看试题解析
6. 为了解某电动车一次充电后行驶的里程数（千米），抽检了10辆车统计结果是：200、210、210、210、220、220、220、220、230、230，则这组数据中众数和中位数分别是（）

A、220，220 B、220，210 C、200，220 D、230，210

查看试题解析
7. 直线 $y = - 3 x + 2$ 经过的象限为（）

A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限

查看试题解析
8. 对于函数 $y = - 3 x + 1$ ，下列结论正确的是（）

A、它的图象必经过点（1，3） B、它的图象经过第一、三、四象限 C、当x＞0时，y＜0 D、y的值随x值的增大而减小

查看试题解析
9. 如图是我国数学家赵爽的股弦图，它由四个全等的直角三角形和小正方形拼成的一个大正方形.已知大正方形的面积是l3，小正方形的面积是1，直角三角形的较短直角边长为a，较长直角边长为b，那么 ${(a + b)}^{2}$ 值为（）

A、25 B、9 C、13 D、169

查看试题解析
10. 小明从家骑车上学，先上坡到达A地后再下坡到达学校，所用的时间与路程如图所示.如果返回时，上下坡的速度仍然保持不变，那么他从学校回到家需要的时间是（）.

A、8.6分钟 B、9分钟 C、12分钟 D、16分钟

查看试题解析

二、填空题

11. 计算：2 $\sqrt{7}$ ﹣6 $\sqrt{7}$ = ．

查看试题解析
12. 新冠病毒的直径是0.000 000 95cm，将0.000 000 95用科学记数法表示为cm.

查看试题解析
13. 已知菱形ABCD的边长为5cm，对角线AC＝6cm，则其面积为cm² ．

查看试题解析
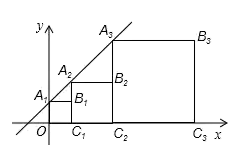14. 正方形 $A_{1} B_{1} C_{1} O 、 A_{2} B_{2} C_{2} C_{1} 、 A_{3} B_{3} C_{3} C_{2} \dots \dots$ 按如图方式放置，点 $A_{1} 、 A_{2} 、 A_{3} \dots \dots$ 和点 $C_{1} 、 C_{2} 、 C_{3} \dots \dots$ 分别在直线 $y = k x + b$ 和 $x$ 轴上，已知点 $B_{1} (1 ， 1) ， B_{2} (3 ， 2)$ ，则 $B_{3}$ 的坐标为.

查看试题解析
15. 两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD＝CD，AB＝CB，晓明同学在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AO＝CO＝ $\frac{1}{2}$ AC；③AC⊥BD；其中，正确的结论有个.

查看试题解析
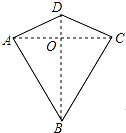16. 如图，从电线杆离地面12m处向地面拉一条长为13m的钢缆，则地面钢缆固定点A到电线杆底部B的距离为．

查看试题解析

三、解答题

17. 计算：

(1)、（2 $\sqrt{3}$ ﹣3 $\sqrt{12}$ +6 $\sqrt{8}$ ）÷2 $\sqrt{2}$

(2)、 $\frac{1}{2} \sqrt{8} - \sqrt{0.5} - \sqrt{4 \frac{1}{2}} + 2 \sqrt{50}$

查看试题解析
18. 已知分式： $(\frac{2 x^{2} + 2 x}{x^{2} - 1} - \frac{x^{2} - x}{x^{2} - 2 x + 1}) \div \frac{x}{x + 1}$ ，解答下列问题：

(1)、化简分式；

(2)、当x=3时，求分式的值；

(3)、原分式的值能等于－1吗？为什么？

查看试题解析
19. 为了解我校学生每周的课外阅读时间情况，随机抽取了八年级部分学生，对学生每周的课外阅读时间x（单位：h）进行分组整理，并绘制了如图所示的不完整的统计图；请根据提供的信息，回答下列问题：

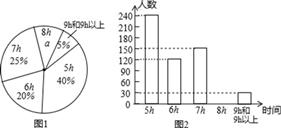(1)、a=▲%，并写出该扇形所对的圆心角的度数为　▲　，请补全条形图.

(2)、在这次抽样调查中，课外阅读时间的众数和中位数分别是多少？

(3)、如果该校共有学生2000人，请你估计该校“课外阅读时间不少于7h”的学生人数大约有多少人？

查看试题解析
20. 如图，▱ABCD的对角线AC、BD相交于点O，过点D作DE∥AC，且DE＝ $\frac{1}{2}$ AC，连接CE、OE

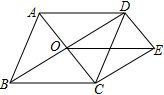(1)、求证：四边形OCED是平行四边形；

(2)、若AD＝DC＝3，求OE的长.

查看试题解析
21. 如图，长方形纸片ABCD中，AB=8，将纸片折叠，使顶点B落在边AD上的E点处，折痕的一端G点在边BC上.

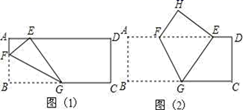(1)、如图（1），当折痕的另一端F在AB边上且AE=4时，求AF的长；

(2)、如图（2），当折痕的另一端F在AD边上且BG=10时，求HF的长.

查看试题解析
22. 今年由于受疫情的影响，引发一系列社会现象，随着疫情的好转，为解决就业、促进民生、拉动内需，国家及时出台地摊经济政策，各地地摊经济如雨后春笋蓬勃发展.长岭中心中学八年级学生郝美丽，最近她每天晚上和妈妈一起去徐家河水库大坝上摆地摊，销售A、B两种电子玩具补贴家用.已知每个A种玩具进价比B种玩具贵4元；且5个A类玩具和2个B类玩具进价共需41元.

(1)、求A、B两种玩具的进价；

(2)、她经实验发现，每天购进这两种玩具共50个，A、B两种玩具售价分别为10元、5元，当天刚好售完.设购进A种玩具x台，两种玩具全部销售完后获得总利润为y元，求y与x之间的函数关系式；

(3)、她每天购买50个玩具的总费用不超过230元；且B类玩具的购买个数不超过A类玩具的4倍.问她采用那种购买方案可获利最大？最大利润是多少元？

查看试题解析
23. 阅读下面问题：
阅读理解：

$\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2}$ ﹣1；

$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；

$\frac{1}{\sqrt{5} + 2} = \frac{1 \times (\sqrt{5} - 2)}{(\sqrt{5} + 2) (\sqrt{5} - 2)} = \sqrt{5} - 2$ .

应用计算：

(1)、 $\frac{1}{\sqrt{7} + \sqrt{6}}$ 的值；

(2)、 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ （n为正整数）的值.
归纳拓展：

(3)、 $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + \dots + \frac{1}{\sqrt{98} + \sqrt{99}} + \frac{1}{\sqrt{99} + \sqrt{100}}$ 的值.

查看试题解析
24. 已知直线y=kx+b经过点A（5，0），B（1，4）.

(1)、求直线AB的解析式；

(2)、若直线y=2x﹣4与直线AB相交于点C，求点C的坐标，并根据图象，直接写出关于x的不等式2x﹣4＞kx+b的解集.

(3)、动点P在y轴上运动，动点Q在x轴上运动，是否存在以P、Q、A、C为顶点，且以AC为边的平行四边形，若存在请求出P点的坐标；若不存在，请说明理由.

查看试题解析