湖北省黄石市经济开发区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-05-24 类型:期末考试
一、单选题
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 以下列各组数据为边长作三角形,其中能组成直角三角形的是( )A、5,12,13 B、3,5,2 C、6,9,14 D、4,10,133. 若一组数据1,4,7,x , 5的平均数为4,则x的值时( )A、7 B、5 C、4 D、34. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数 与方差 :
甲
乙
丙
丁
平均数 ( )
175
173
175
174
方差 ( )
3.5
3.5
12.5
15
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁6. 下列命题中,真命题是( )A、有两边相等的平行四边形是菱形 B、有一个角是直角的四边形是矩形 C、四个角相等的菱形是正方形 D、两条对角线互相垂直且相等的四边形是正方形7. 已知正比例函数y=kx,且y随x的增大而减少,则直线y=2x+k的图象是( )A、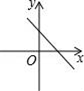 B、
B、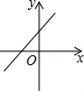 C、
C、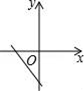 D、
D、 8. 如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( )
8. 如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( ) A、3 B、4 C、5 D、69. 如图,过平行四边形ABCD对角线交点O的线段EF , 分别交AD , BC于点E , F , 当AE=ED时,△AOE的面积为4,则四边形EFCD的面积是( )
A、3 B、4 C、5 D、69. 如图,过平行四边形ABCD对角线交点O的线段EF , 分别交AD , BC于点E , F , 当AE=ED时,△AOE的面积为4,则四边形EFCD的面积是( ) A、8 B、12 C、16 D、3210. 如图,在平面直角坐标系中,点 , , 在直线 上,点 , , 在x轴上, , , 都是等腰直角三角形,若已知点 ,则点 的纵坐标是( )
A、8 B、12 C、16 D、3210. 如图,在平面直角坐标系中,点 , , 在直线 上,点 , , 在x轴上, , , 都是等腰直角三角形,若已知点 ,则点 的纵坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
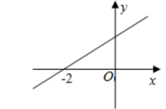
11. 若式子x+ 在实数范围内有意义,则x的取值范围是 .12. 若一直角三角形的两直角边长为 ,1,则斜边长为 .13. 把直线y=﹣x﹣1沿着y轴向上平移2个单位,所得直线的函数解析式为 .14. 如图,直线 与x轴的交点为 ,则关于x的不等式 的解集是.
 15. 如图,平行四边形ABCD在平面直角坐标系中,已知∠DAB=60°,A(﹣2,0),点P在AD上,连接PO , 当OP⊥AD时,点P到y轴的距离为 .
15. 如图,平行四边形ABCD在平面直角坐标系中,已知∠DAB=60°,A(﹣2,0),点P在AD上,连接PO , 当OP⊥AD时,点P到y轴的距离为 .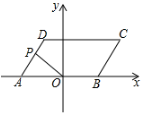 16. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为.
16. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为.
三、解答题
-
17.(1)、计算:(2)、计算: .18. 如图,△ABC中,AB=AC , BC=4cm , 作AD⊥BC , 垂足为D , 若AD=4cm , 求AB的长.
 19. 如图,已知平行四边形 的对角线 和 交于点O,且 , ,求 的周长.
19. 如图,已知平行四边形 的对角线 和 交于点O,且 , ,求 的周长. 20. 某校八年级学生在一次射击训练中,随机抽取10名学生的成绩如下表,请回答问题:
20. 某校八年级学生在一次射击训练中,随机抽取10名学生的成绩如下表,请回答问题:环数
6
7
8
9
人数
1
5
2
(1)、填空:10名学生的射击成绩的众数是 , 中位数是 .(2)、求这10名学生的平均成绩.(3)、若9环(含9环)以上评为优秀射手,试估计全年级500名学生中有多少是优秀射手?21. 如图,菱形 的对角线 、 相交于点O, , , 与 交于点F.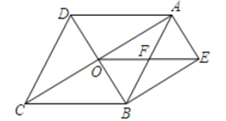 (1)、试判断四边形 的形状,并说明理由;(2)、若 , ,求菱形 的面积.22. 在平面直角坐标系中,原点为O,已知一次函数的图象过点A(0,5),点B(-1,4)和点P(m,n).(1)、求这个一次函数的解析式;(2)、当n=2时,求直线AB,直线OP与x轴围成的图形的面积;(3)、当 的面积等于 的面积的2倍时,求n的值.23. 某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.(1)、设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;(2)、经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元( ),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
(1)、试判断四边形 的形状,并说明理由;(2)、若 , ,求菱形 的面积.22. 在平面直角坐标系中,原点为O,已知一次函数的图象过点A(0,5),点B(-1,4)和点P(m,n).(1)、求这个一次函数的解析式;(2)、当n=2时,求直线AB,直线OP与x轴围成的图形的面积;(3)、当 的面积等于 的面积的2倍时,求n的值.23. 某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.(1)、设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;(2)、经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元( ),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.