湖北省黄冈麻城市2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算一定正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $- 2 \sqrt{3} = \sqrt{2^{2} \times 3} = \sqrt{12}$ C、 $\sqrt{a^{2}} = a$ D、 $| \sqrt{3} - 2 | = 2 - \sqrt{3}$

查看试题解析
2. 在趣味运动会“定点投篮”项目中，我校七年级八个班的投篮成绩（单位：个）分别为：24，20，19，20，22，23，20，22.则这组数据中的众数和中位数分别是（　　）

A、22个、20个 B、22个、21个 C、20个、21个 D、20个、22个

查看试题解析
3. 已知函数 $y = x - 3$ ，若当 $x = a$ 时， $y = 5$ ；当 $x = b$ 时， $y = 3$ ，a 和 b 的大小关系是（）

A、 $a > b$ B、 $a < b$ C、 $a = b$ D、不能确定

查看试题解析
4. 某公司手机话费收费有 A 套餐（月租费 $15$ 元，通话费每分钟 $0.1$ 元）和 B 套餐（月租费 $0$ 元，通话费每分钟 $0.15$ 元）两种.当月通话时间为（）时，A，B 两种套餐收费一样.

A、 $100$ 分钟 B、 $200$ 分钟 C、 $300$ 分钟 D、 $400$ 分钟

查看试题解析
5. 如图，“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形，若直角三角形的两直角边长分别为5和3，则小正方形的面积为（）

A、4 B、3 C、2 D、1

查看试题解析
6. 如图，函数y=kx+b（k≠0）的图象经过点B（2，0），与函数y=2x的图象交于点A ，则不等式0＜kx+b＜2x的解集为（）

A、 $1 < x < 2$ B、 $x > 2$ C、 $x > 0$ D、 $0 < x < 1$

查看试题解析
7. 如图，正方形 $A B C D$ 中， $A B = 4$ ，E 是 $B C$ 的中点，点 P 是对角线 $A C$ 上一动点，则 $P E + P B$ 的最小值为（）

A、4 B、 $2 \sqrt{5}$ C、 $4 \sqrt{2}$ D、 $4 \sqrt{3}$

查看试题解析
8. 如图，平行四边形ABCD的周长是26cm，对角线AC与BD交于点O，AC⊥AB，E是BC中点，△AOD的周长比△AOB的周长多3cm，则AE的长度为（）

A、3cm B、4cm C、5cm D、8cm

查看试题解析

二、填空题

9. 若 $\sqrt{2 x - 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
10. 为从甲乙两名射击运动员中选出一人参加竞标赛，特统计了他们最近10次射击训练的成绩，其中，他们射击的平均成绩为8.9环，方差分别是 $S_{甲}^{2} = 0.8 ， S_{乙}^{2} = 1.3$ ，从稳定性的角度看，的成绩更稳定．（填“甲”或“乙”）

查看试题解析
11. 某大学自主招生考试只考数学和物理，计算综合得分时，按数学占60%，物理点40%计算.已知孔明数学得分为95分，综合得分为93分，那么孔明物理得分是分.

查看试题解析
12. 一次函数y=kx+b与y=2x+1平行，且经过点（﹣3，4），则表达式为：．

查看试题解析
13. 在全民健身环城越野赛中，甲、乙两名选手的行程y（千米）随时间t（时）变化的图象（全程）如图所示.有下列说法：①起跑后1小时内，甲在乙的前面；②第1小时两人都跑了10千米；③甲比乙先到达终点；④两人都跑了20km.其中正确的说法有.

查看试题解析
14. 如图，在平行四边形ABCD中，DE平分∠ADC，AD=6，BE=2，则平行四边形ABCD的周长是．

查看试题解析
15. 如图，在矩形 $A B C D$ 中，点 E，F 分别在边 $A B$ ， $B C$ 上，且 $A E = \frac{1}{3} A B$ ，将矩形沿直线 $E F$ 折叠，点 B 恰好落在 $A D$ 边上的点 P 处，连接 $B P$ 交 $E F$ 于点 Q，则线段QF与QE的长度关系为.

查看试题解析
16. 如图，在周长为8的菱形 $A B C D$ 中，已知 $∠ D A C = 45 °$ ，点O为对角线 $A C$ 的中点，过点O作射线 $O M$ ， $O N$ 分别交 $A B$ ， $B C$ 于点E，F，且 $∠ E O F = 90 °$ ，则 $Δ A E O$ 和 $Δ C F O$ 的面积和为.

查看试题解析

三、解答题

17.

(1)、计算： ${(- \sqrt{5})}^{2} + 3 \sqrt{3} \times \sqrt{12}$ .

(2)、已知 $x = \sqrt{5} - 1$ ，求代数式 $x^{2} + 5 x - 6$ 的值.

查看试题解析
18. 先阅读下面的解题过程，然后再解答.形如 $\sqrt{m \pm 2 \sqrt{n}}$ 的化简，我们只要找到两个数a，b，使 $a + b = m$ ， $a b = n$ ，即 ${(\sqrt{a})}^{2} + {(\sqrt{b})}^{2} = m$ ， $\sqrt{a} \cdot \sqrt{b} = \sqrt{n}$ ，那么便有： $\sqrt{m \pm 2 \sqrt{n}} = \sqrt{{(\sqrt{a} \pm \sqrt{b})}^{2}} = \sqrt{a} \pm \sqrt{b} (a > b ⩾ 0)$ .
例如化简： $\sqrt{7 + 4 \sqrt{3}}$ .

解：首先把 $\sqrt{7 + 4 \sqrt{3}}$ 化为 $\sqrt{7 + 2 \sqrt{12}}$ ，

这里 $m = 7$ ， $n = 12$ ，

由于 $4 + 3 = 7$ ， $4 \times 3 = 12$ ，

所以 ${(\sqrt{4})}^{2} + {(\sqrt{3})}^{2} = 7, \sqrt{4} \times \sqrt{3} = \sqrt{12}$ ，

所以 $\sqrt{7 + 4 \sqrt{3}} = \sqrt{7 + 2 \sqrt{12}} = \sqrt{{(\sqrt{4} + \sqrt{3})}^{2}} = 2 + \sqrt{3}$ .

根据上述方法化简： $\sqrt{13 - 2 \sqrt{42}}$ .

查看试题解析
19. 如图，直线 $y = k x + 8$ 分别与 x 轴，y 轴相交于 A，B 两点，O 为坐标原点，A 点的坐标为 $(4 ， 0)$ .

(1)、求 k 的值；

(2)、过线段 $A B$ 上一点 P（不与端点重合）作 x 轴，y 轴的垂线，垂足分别为 M，N.当长方形 $P M O N$ 的周长是 10 时，求点 P 的坐标.

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = 4$ ， $A C = 3$ ， $B C = 5$ ， $D E$ 是 $B C$ 的垂直平分线， $D E$ 分别交 $B C$ 、 $A B$ 于点D、E.

(1)、说明： $△ A B C$ 为直角三角形.

(2)、求 $A E$ 的长.

查看试题解析
21. 如图，矩形ABCD中，E是AD的中点，延长CE、BA交于点F，连接AC、DF．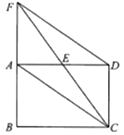

(1)、求证：四边形ACDF是平行四边形；

(2)、当CF平分∠BCD时，写出BC与CD的数量关系，并说明理由．

查看试题解析

22. 某中学举行“校园好声音”歌手大赛，初、高中部根据初赛成绩，各选出

5

名选手组成初中代表队和高中代表队参加学校决赛.每个队

5

名选手的决赛成绩如图所示：

(1)、填表：

	平均数（分）	中位数（分）	众数（分）
初中代表队	85	85
高中代表队	85		100

(2)、结合两队决赛成绩的平均数和中位数，分析哪个代表队的成绩较好；

(3)、计算两队决赛成绩的方差，并判断哪个代表队的成绩较为稳定.

查看试题解析

23. 某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．

(1)、求每台A型电脑和B型电脑的销售利润；

(2)、该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；

②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？最大利润是多少？

查看试题解析
24. 如图，四边形 $A B C D$ 是正方形，M是边 $B C$ 上一点，E是 $C D$ 的中点， $A E$ 平分 $∠ D A M$ .

(1)、判断 $∠ A M B$ 与 $∠ M A E$ 的数量关系，并说明理由；

(2)、求证： $A M = A D + M C$ ；

(3)、若 $A D = 4$ ，求 $A M$ 的长.

查看试题解析
25. 在平面直角坐标系中，点 $A (0 ， b)$ ，点 $B (a ， 0)$ ，点 $D (d ， 0)$ 且 a，b，d 满足 $\sqrt{a + 1} + \sqrt{b - 3} + {(2 - d)}^{2} = 0$ ， $D E ⊥ x$ 轴且 $∠ B E D = ∠ A B D$ ， $B E$ 交 y 轴于点 C， $A E$ 交 x 轴于点 F.

(1)、求点 A，B，D 的坐标；

(2)、求点 E，F 的坐标；

(3)、如图，过 $P (0 ， - 1)$ 作 x 轴的平行线，在该平行线上有一点 Q（点 Q 在 P 的右侧）使 $∠ Q E M = 45^{\circ}$ ， $Q E$ 交 x 轴于 N， $M E$ 交 y 轴正半轴于 M，求 $\frac{A M - M Q}{P Q}$ 的值.

查看试题解析