湖北省丹江口市2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子一定是二次根式的是（）

A、 $\sqrt{a^{2}}$ B、－ $\sqrt{a}$ C、 $\sqrt[3]{a}$ D、 $\sqrt{a}$

查看试题解析
2. 下列运算中，正确的是（）

A、5 $\sqrt{3}$ －2 $\sqrt{3}$ =3 B、2 $\sqrt{2}$ ×3 $\sqrt{2}$ =6 C、3 $\sqrt{3}$ ÷ $\sqrt{3}$ =3 D、2 $\sqrt{3}$ ＋3 $\sqrt{2}$ =5 $\sqrt{5}$

查看试题解析
3. 下列四组数据不能作为直角三角形的三边长的是（）

A、6，8，10 B、5，12，13 C、3，5，6 D、 $\sqrt{2}$ ， $\sqrt{3}$ ， $\sqrt{5}$

查看试题解析
4. 下列说法中错误的是（）

A、一组数据的平均数受极端值的影响较大 B、一组数据的平均数、众数、中位数有可能相同 C、如果一组数据的众数是5，那么这组数据中出现次数最多的数据是5 D、一组数据的中位数有时有两个

查看试题解析
5. 能判定一个四边形是平行四边形的条件是（）

A、一组对角相等 B、两条对角线互相平分 C、一组对边相等 D、两条对角线互相垂直

查看试题解析
6. 已知直线y＝2x＋b，当b＜0时，该直线不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 在Rt△ABC中，∠C＝90°，其中一个锐角为30°，最短边长为5cm，则最长边上的中线是( 　 )

A、5cm B、2.5cm C、10cm D、15cm

查看试题解析
8. 如图，是一张直角三角形的纸片，两直角边 $A C = 6 ， B C = 8$ ，现将 $△ A B C$ 折叠，使点B点A重合，折痕为DE，则BD的长为（）

A、7 B、 $\frac{25}{4}$ C、6 D、 $\frac{11}{2}$

查看试题解析
9. 甲、乙两车从 $A$ 城出发匀速行驶至 $B$ 城.在整个行驶过程中，甲、乙两车离 $A$ 城的距离 $y$ (千米)与甲车行驶的时间 $t$ (小时)之间的函数关系如图所示.则下列结论：
① $A ， B$ 两城相距 $300$ 千米；②乙车比甲车晚出发 $1$ 小时，却早到 $1$ 小时；③乙车出发后 $2.5$ 小时追上甲车；④当甲、乙两车相距 $50$ 千米时， $t = \frac{5}{4} 或 \frac{15}{4}$ 其中正确的结论有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
10. 如图，在正方形OABC中，点B的坐标是(6，6)，点E，F分别在边BC，BA上，OE=3 $\sqrt{5}$ .若∠EOF=45°，则F点的纵坐标是（）

A、2 B、 $\frac{5}{3}$ C、 $\sqrt{3}$ D、 $\sqrt{5}$ －1

查看试题解析

二、填空题

11. 若式子 $\sqrt{1 - x}$ 在实数范围内有意义，则x的取值范围是.

查看试题解析
12. 在一次数学答题比赛中，六位同学答对题目的个数分别为7，5，3，7，5，10，则这组数据的众数是.

查看试题解析
13. 如图，已知两正方形的面积分别是25和169，则字母B所代表的正方形的边长是。

查看试题解析
14. 已知一次函数y=kx+2k+3的图象与y轴的交点在y轴的正半轴上，且函数值y随x的增大而减小，则k所能取到的整数值为．

查看试题解析
15. 如图，在Rt△ABC中，∠BAC=90°，且BA=9，AC=12，点D是斜边BC上的一个动点，过点D分别作DE⊥AB于点E，DF⊥AC于点F，点G为四边形DEAF对角线交点，则线段GF的最小值为.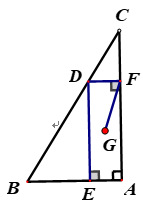

查看试题解析
16. 如图，正方形ABCD对角线相交于点O，CP⊥DP于P，CP＝5，DP＝7，则△POD面积为.

查看试题解析

三、解答题

17. 计算： $(2 + \sqrt{3}) (2 - \sqrt{3}) - | \sqrt{3} - 2 | + {(\sqrt{3} + 1)}^{0}$

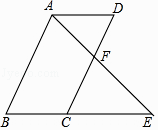
查看试题解析
18. 如图，四边形ABCD为平行四边形，F是CD的中点，连接AF并延长与BC的延长线交于点E．求证：BC=CE．

查看试题解析
19. 已知y＋3与x成正比例，且x＝2时，y＝7.

(1)、求y与x的函数关系式；

(2)、将所得函数图象平移，使它过点(0，3)，求平移后直线的解析式.

查看试题解析
20. 如图，一架长25米的梯子，斜靠在竖直的墙上，这时梯子底端离墙7米．

(1)、此时梯子顶端离地面多少米？

(2)、若梯子顶端下滑4米，那么梯子底端将向左滑动多少米？

查看试题解析
21. 某单位若干名职工参加“预防新冠肺炎”卫生知识竞赛，将成绩制成如图所示的扇形统计图和条形统计图，根据图中提供的信息，求这些职工成绩的中位数和平均数.

查看试题解析
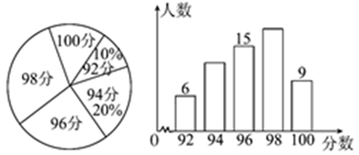22. 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F.

(1)、若∠B＝30°，AC＝4，求CE的长；

(2)、过点F作AB的垂线，垂足为G，连接EG，试判断四边形CEGF的形状，并说明理由.

查看试题解析
23. 如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量 $y$ （千瓦时）关于已行驶路程 $x$ （千米）的函数图象.

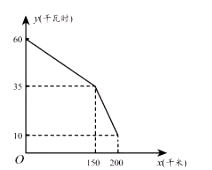(1)、根据图象，直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程，当 $0 \leq x \leq 150$ 时，求1千瓦时的电量汽车能行驶的路程；

(2)、当 $150 \leq x \leq 200$ 时求 $y$ 关于 $x$ 的函数表达式，并计算当汽车已行驶180千米时，蓄电池的剩余电量.

查看试题解析
24. 如图1，点O是菱形ABCD对角线的交点，点P是对角线AC上一动点，过点P作PE⊥直线AD于E，PF⊥直线CD于F，AB＝10，AC＝16.

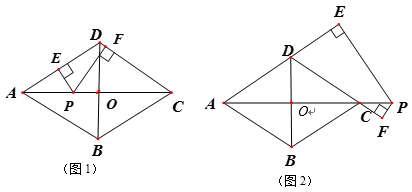(1)、填空：BD＝；

(2)、点P在运动过程中，PE＋PF的值是否发生变化？若不变，请求出PE＋PF的值；若变化，请说明理由；

(3)、如图2，若点P在线段AC延长线上运动时，求PE－PF的值.

查看试题解析
25. 如图，直线y＝ $\frac{1}{2}$ x－3分别与x轴，y轴交于点A，B两点，直线y＝－x交直线AB于点C，点P从点O出发，以每秒1个单位的速度向点A匀速运动.

(1)、求点C坐标；

(2)、若△COP是等腰三角形，求点P运动时间；

(3)、当直线CP平分△OAC的面积时，直线CP与y轴交于点D，求线段CD的长.

查看试题解析