初中数学北师大版八年级下学期 第六章 单元测试卷
试卷更新日期：2021-05-24 类型：单元试卷
一、单选题
-
1. 六边形的外角和为（ ）A、180° B、360° C、720° D、1080°2. 一个n边形的每个外角都是45°，则这个n边形的内角和是（ ）A、1080° B、540° C、2700° D、2160°3. 在平行四边形 中，若 ，则 的度数是（ ）A、50° B、60° C、70° D、80°4. 如图所示，在平行四边形ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于（ ）
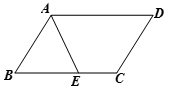A、2 cm B、3 cm C、4 cm D、5 cm5. 如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是（ ）
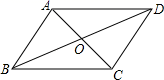A、AB∥CD，AD∥BC B、AD∥BC，AB＝CD C、OA＝OC，OB＝OD D、AB＝CD，AD＝BC6. 如图 是正五边形 的三个外角，若 则 =（ ）
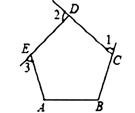A、 B、 C、 D、7. 一个四边形，截一刀后得到的新多边形的内角和将（ ）A、增加180° B、减少180° C、不变 D、以上三种情况都有可能8. 如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF，CF，则下列结论中不一定成立的是（ ）
A、S△BEC=2S△CEF B、EF=CF C、∠DCF= ∠BCD D、∠DFE=3∠AEF二、填空题
-
9. 一个正多边形的内角和为 ，则这个多边形的外角的度数为.10. 如图，小亮从点A出发，沿直线前进15米后向左转30°，再沿直线前进15米，又向左转30°…… 照这样走下去，他第一次回到出发地点A时，共走了米．
11. 若多边形的内角和是外角和的2倍，则该多边形是边形.12. 某多边形的内角和是 ，从这个多边形的一个顶点出发可以作条对角线.13. 如图，□ 的周长为 ， 相交于点 ， 交 于 ，则 的周长为 .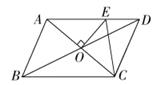
14. 如图，AB＝AC，四边形AEDF是平行四边形，△CFD和△DEB的周长分别为5和10，则△ABC的周长是.
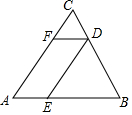15. 如图，平行四边形ABCD中，AB=8cm，AD=12cm，点P在AD边上以每秒1cm的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在运动以后，以P、D、Q、B四点组成平行四边形的次数有次.
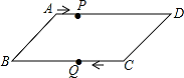16. 如图，在 中， ， ， ，过点A作 且点F在点A的右侧.点D从点A出发沿射线AF方向以 /秒的速度运动，同时点P从点E出发沿射线EB方向以 /秒的速度运动，在线段PE上取点C，使得 ，设点D的运动时间为 秒.当 秒时，以A，B，C，D为顶点的四边形是平行四边形.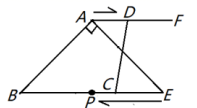
三、解答题
-
17. 如图，在平行四边形 中， .
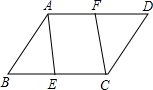
求证： .
18. 如图，在平行四边形 中， 分别是 的中点．求证： ．
19. 如图，点 ， 是四边形 的对角线 上的两点，且 ， ， ．求证： ．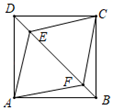
20. 多边形的内角和与某一外角的度数总和为1 350°，那么这个多边形的边数是多少？21. 一个正多边形的每一个内角比每一个外角的5倍还小60°，求这个正多边形的边数及内角和.22. 如图，四边形 ABCD 和四边形 CDEF 均为平行四边形，连接 AE，BF.求证：AE=BF.
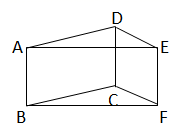23. 已知，如图，点P是平行四边形ABCD外一点，PE∥AB交BC于点E． PA、PD分别交BC于点M、N，点M是BE的中点．求证：CN＝EN．
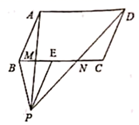24. 如图，DE是△ABC的中位线，延长DE到F，使EF=DE，连接BF．求证：BF=DC；
25. 如图所示，在四边形ABCD中，AD∥BC，AD=24cm ， BC=30cm ， 点P从A向点D以1cm/s的速度运动，到点D即停止．点Q从点C向点B以2cm/s的速度运动，到点B即停止．直线PQ将四边形ABCD截得两个四边形，分别为四边形ABQP和四边形PQCD，则当P，Q两点同时出发，几秒后所截得两个四边形中，其中一个四边形为平行四边形？
26. 已知四边形ABCD的对角线AC与BD交于点O，给出下列四个论断① OA＝OC ② AB＝CD ③ ∠BAD＝∠DCB ④ AD∥BC
请你从中选择两个论断作为条件，以“四边形ABCD为平行四边形”作为结论，完成下列各题：
(1)、构造一个真命题，画图并给出证明；
(2)、构造一个假命题，举反例加以说明.