浙江省备考2021年中考数学模拟试卷(丽水市)
试卷更新日期:2021-05-22 类型:中考模拟
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 的相反数是( )A、-3 B、3 C、- D、2. 若分式 的值为0,则x的值为( )A、﹣2 B、0 C、2 D、±23. 下列各式中能用平方差公式计算的是( )A、 B、 C、 D、4. 下列图形是中心对称图形的是( )A、
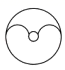 B、
B、 C、
C、 D、
D、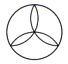 5. 小明将分别标有爱我中华汉字的四个小球装在一个不透明的口袋中,这些球除汉字外都相同,每次摸球前先搅拌均匀,随机摸出一球记下汉字后放回,再随机摸出一球,两次摸出的球上的汉字能组成“中华”的概率是( )A、 B、 C、 D、6. 将一副三角板和一张对边平行的纸条按如图摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
5. 小明将分别标有爱我中华汉字的四个小球装在一个不透明的口袋中,这些球除汉字外都相同,每次摸球前先搅拌均匀,随机摸出一球记下汉字后放回,再随机摸出一球,两次摸出的球上的汉字能组成“中华”的概率是( )A、 B、 C、 D、6. 将一副三角板和一张对边平行的纸条按如图摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( ) A、15° B、22.5° C、30° D、45°7. 如图是反比例函数 的图象在第二象限内的一个分支,则下列说法错误的是( )
A、15° B、22.5° C、30° D、45°7. 如图是反比例函数 的图象在第二象限内的一个分支,则下列说法错误的是( ) A、另一个分支在第四象限内 B、常数 C、在每个象限内,y随x的增大而增大 D、若A(-1,h),B(2,k) 在图象上,则h k8. 如图, 内接于⊙O, , ,则⊙O的半径为( )
A、另一个分支在第四象限内 B、常数 C、在每个象限内,y随x的增大而增大 D、若A(-1,h),B(2,k) 在图象上,则h k8. 如图, 内接于⊙O, , ,则⊙O的半径为( ) A、 B、 C、2 D、49. 我国古代《孙子算经》记载“多人共车”问题:“今有三人共车,二车空;二人共车,九人步问人与车各几何?”意思是说“每三人共乘一辆车,最终剩余2辆车;每2人共乘一辆车,最终有9人无车可乘.问人和车的数量各是多少?”若设有x个人,则可列方程是( )A、3(x+2)=2x﹣9 B、3(x﹣2)=2x+9 C、 +2= D、 ﹣2=10. 图1是我国著名的“赵爽弦图”,它是由四个全等的直角三角形所围成.将四个直角三角形的较短边(如 )向外延长1倍得到点 , , , ,并连结得到图2.已知正方形 与正方形 的面积分别为 和 ,则图2中阴影部分的面积是( )
A、 B、 C、2 D、49. 我国古代《孙子算经》记载“多人共车”问题:“今有三人共车,二车空;二人共车,九人步问人与车各几何?”意思是说“每三人共乘一辆车,最终剩余2辆车;每2人共乘一辆车,最终有9人无车可乘.问人和车的数量各是多少?”若设有x个人,则可列方程是( )A、3(x+2)=2x﹣9 B、3(x﹣2)=2x+9 C、 +2= D、 ﹣2=10. 图1是我国著名的“赵爽弦图”,它是由四个全等的直角三角形所围成.将四个直角三角形的较短边(如 )向外延长1倍得到点 , , , ,并连结得到图2.已知正方形 与正方形 的面积分别为 和 ,则图2中阴影部分的面积是( )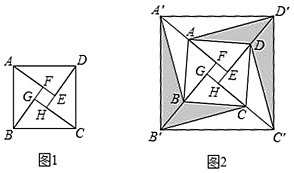 A、 B、 C、 D、
A、 B、 C、 D、二、填空题 (本题有6小题,每小题4分,共24分)
-
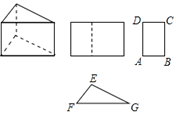
11. 若点(2,m﹣3)在第四象限,则实数m的取值范围是.12. 一组数据:16,5,11,9,5的中位数是.13. 三棱柱的三视图如图所示,已知△EFG中,EF=8cm,EG=12cm,∠EFG=45°.则AB的长为cm.
 14. 已知:在平行四边形ABCD中,点E在DA的延长线上,AE= AD,连接CE交BD于点F,则 的值是 .
14. 已知:在平行四边形ABCD中,点E在DA的延长线上,AE= AD,连接CE交BD于点F,则 的值是 . 15. 如图,正六边形ABCDEF外接圆的半径为4,则其内切圆的半径是 .
15. 如图,正六边形ABCDEF外接圆的半径为4,则其内切圆的半径是 .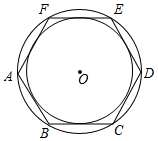 16. 如图,将△ABC沿BC翻折得到△DBC,再将△DBC绕C点逆时针旋转60°得到△FEC,延长BD交EF于H,已知∠ABC=30°,∠BAC=90°,AC=1,则四边形CDHF的面积为 .
16. 如图,将△ABC沿BC翻折得到△DBC,再将△DBC绕C点逆时针旋转60°得到△FEC,延长BD交EF于H,已知∠ABC=30°,∠BAC=90°,AC=1,则四边形CDHF的面积为 .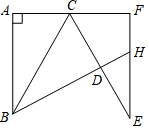
三、解答题 (本题有8小题,共66分,各小题都必须写出解答过程)
-
17. 计算: +|1﹣ |﹣2sin60°+(π﹣2016)0﹣ .18. 解不等式: ﹣ ≤119. 某茶农要对1号、2号、3号、4号四个品种共500株茶树幼苗进行成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号茶树幼苗成活率为89.6%,把实验数据绘制成图1和图2所示的两幅不完整的统计图.
 (1)、实验所用的2号茶树幼苗的数量是株;(2)、求出3号茶树幼苗的成活数,并补全统计图2;(3)、该茶农要从这四种茶树中选择两个品种进行推广,请用列表或画树状图的方法求出1号品种被选中的概率.20. 如图,BC为⊙O直径,点A是⊙O上任意一点(不与点B、C重合),以BC、AB为邻边的平行四边形ABCD的顶点D在⊙O外.
(1)、实验所用的2号茶树幼苗的数量是株;(2)、求出3号茶树幼苗的成活数,并补全统计图2;(3)、该茶农要从这四种茶树中选择两个品种进行推广,请用列表或画树状图的方法求出1号品种被选中的概率.20. 如图,BC为⊙O直径,点A是⊙O上任意一点(不与点B、C重合),以BC、AB为邻边的平行四边形ABCD的顶点D在⊙O外. (1)、当AD与⊙O相切时,求∠B的大小.(2)、若⊙O的半径为2,BC=2AB,直接写出 的长.21. 为了更好地做好复课准备,某班家委会讨论决定购买A,B两种型号的口罩供班级学生使用,已知A型口罩每包价格a元,B型口罩每包价格比A型少4元,180元钱购买的A型口罩比B型口罩少12包。(1)、求a的值。(2)、经与商家协商,购买A型口罩价格可以优惠,其中每包价格y(元)和购买数量x(包)的函数关系如图所示,B型口罩一律按原价销售。
(1)、当AD与⊙O相切时,求∠B的大小.(2)、若⊙O的半径为2,BC=2AB,直接写出 的长.21. 为了更好地做好复课准备,某班家委会讨论决定购买A,B两种型号的口罩供班级学生使用,已知A型口罩每包价格a元,B型口罩每包价格比A型少4元,180元钱购买的A型口罩比B型口罩少12包。(1)、求a的值。(2)、经与商家协商,购买A型口罩价格可以优惠,其中每包价格y(元)和购买数量x(包)的函数关系如图所示,B型口罩一律按原价销售。
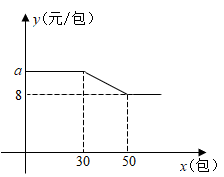
①求y关于x的函数解析式;
②若家委会计划购买A型、B型共计100包,其中A型不少于30包,且不超过60包。问购买A型口罩多少包时,购买口罩的总金额最少,最少为多少元?
22. 如图 (1)、问题发现
(1)、问题发现如图1,△ABC与△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,直线BD,CE交于点F,直线BD,AC交于点G.则线段BD和CE的数量关系是 , 位置关系是;
(2)、类比探究如图2,在△ABC和△ADE中,∠ABC=∠ADE=α,∠ACB=∠AED=β,直线BD,CE交于点F,AC与BD相交于点G.若AB=kAC,试判断线段BD和CE的数量关系以及直线BD和CE相交所成的较小角的度数,并说明理由;
(3)、拓展延伸如图3,在平面直角坐标系中,点M的坐标为(3.0),点N为y轴上一动点,连接MN.将线段MN绕点M逆时针旋转90得到线段MP,连接NP,OP.请直接写出线段OP长度的最小值及此时点N的坐标.
23. 如图,二次函数 的图象交x轴于A,B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4). (1)、求二次函数的解析式和直线BD的解析式;(2)、点p是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B,D的点Q,使 中BD边上的高为 ,若存在求出点Q的坐标;若不存在请说明理由.24. 如图,已知⊙C过菱形ABCD的三个顶点B,A,D,连结BD,过点A作AE∥BD交射线CB于点E.
(1)、求二次函数的解析式和直线BD的解析式;(2)、点p是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B,D的点Q,使 中BD边上的高为 ,若存在求出点Q的坐标;若不存在请说明理由.24. 如图,已知⊙C过菱形ABCD的三个顶点B,A,D,连结BD,过点A作AE∥BD交射线CB于点E.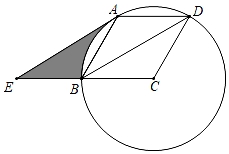 (1)、求证:AE是⊙C的切线.(2)、若半径为2,求图中线段AE、线段BE和 围成的部分的面积.(3)、在(2)的条件下,在⊙C上取点F,连结AF,使∠DAF=15°,求点F到直线AD的距离.
(1)、求证:AE是⊙C的切线.(2)、若半径为2,求图中线段AE、线段BE和 围成的部分的面积.(3)、在(2)的条件下,在⊙C上取点F,连结AF,使∠DAF=15°,求点F到直线AD的距离.