浙江省备考2021年中考数学模拟试卷（金华市）

试卷更新日期：2021-05-22 类型：中考模拟

进入出卷网下载

一、选择题(本题有10小题,每小题3分,共30分)

1. $3$ 的相反数是（　　）

A、 $- 3$ B、 $\sqrt{3}$ C、 $3$ D、 $\pm 3$

查看试题解析
2. 若分式 $\frac{x^{2} - x - 2}{x + 1}$ 的值为0，则x的值为（）

A、 $x = 1$ 或 $x = 2$ B、 $x = 0$ C、 $x = 2$ D、 $x = - 1$

查看试题解析
3. 选择计算 $(- 4 x^{2} + 3 y) (4 x^{2} + 3 y)$ 的最佳方法是（）

A、运用多项式乘多项式法则 B、运用平方差公式 C、运用单项式乘多项式法则 D、运用完全平方公式

查看试题解析
4. 下列四个图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 从箱子中摸出红球的概率为 $\frac{1}{4}$ ，已知口袋中红球有 $4$ 个，则袋中共有球（）个

A、 $24$ B、 $16$ C、 $8$ D、 $4$

查看试题解析
6. 如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是（）

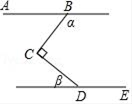A、α+β＝180° B、α+β＝90° C、β＝3α D、α﹣β＝90°

查看试题解析
7. 若点A（x₁ ， y₁），B（x₂ ， y₂），和C（x₃ ， y₃），分别在反比例函数 $y = \frac{6}{x}$ 的图象上，且x₁＜x₂＜0＜x₃ ，则下列判断中正确的是（）

A、y₁＜y₂＜y₃ B、y₂＜y₁＜y₃ C、y₃＜y₂＜y₁ D、y₂＜y₃＜y₁

查看试题解析
8. 如图，A，B，C三点在圆上，在△ABC中，∠ABC=70°，∠ACB=30°，D是弧BAC的中点，连结DB，DC，则∠DBC的度数为（　　）

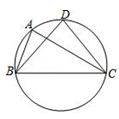A、70° B、50° C、45° D、30°

查看试题解析
9. 小明和小亮两人在长为50m的直道AB（A、B为直道两端点）上进行匀速往返跑训练，两人同时从A点起跑，到达B点后，立即转身跑向A点，到达A点后，又立即转身跑向B点……若小明跑步速度为5m/s，小亮跑步速度为4m/s，则起跑后60s内，两人相遇的次数为（）

A、3 B、4 C、5 D、6

查看试题解析
10. 如图，四个全等的直角三角形拼成“赵爽弦图”得到正方形ABCD与正方形EFGH.连结EG，BD相交于点O，BD与HC相交于点P.若 $G O = G P$ ，下列结论：① $∠ G O P = ∠ B C P$ ，② $B C = B P$ ，③ $B G ： P G = \sqrt{2} + 1$ ，④ $D P = P O$ .正确的是（）

A、②③④ B、①③④ C、①②④ D、①②③

查看试题解析

二、填空题 (本题有6小题,每小题4分,共24分)

11. 在平面直角坐标系中，点A（2，﹣3）位于第象限．

查看试题解析
12. 已知一组数据3，4，4，2，5，这组数据的中位数为

查看试题解析
13. 如图是某圆锥的主视图和左视图，该圆锥的侧面积是.

查看试题解析
14. 如图，已知▱ABCD的对角线AC，BD交于点O，且AC=8，BD=10，AB=5，则△OCD的周长为.

查看试题解析
15. 如图，正六边形ABCDEF内接于 $⊙ O$ ，半径为4，则这个正六边形的边心距OM的长为．

查看试题解析
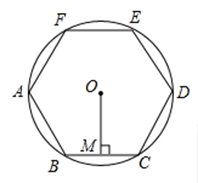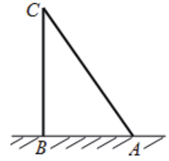
16. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中记载了一个“折竹抵地”问题：“今有竹高二丈，末折抵地，去本六尺，问折者高几何？”
译文：“有一根竹子，原高二丈（1丈=10尺），现被风折断，竹梢触地面处与竹根的距离为6尺，问折断处离地面的高度为多少尺？”

如图，我们用点 $A ， B ， C$ 分别表示竹梢，竹根和折断处，设折断处离地面的高度 $B C$ 为x尺，则可列方程为．

查看试题解析

三、解答题 (本题有8小题,共66分,各小题都必须写出解答过程)

17. 计算：3cos60°﹣2^﹣1+（π﹣3）⁰﹣ $\sqrt{{(- 2)}^{2}}$ ．

查看试题解析
18. 解不等式： $2 (x - 1) + 4 > 0$

查看试题解析
19. 某企业工会开展“一周工作量完成情况”调查活动，随机调查了部分员工一周的工作量剩余情况，并将调查结果统计后绘制成如图1和图2所示的不完整统计图．

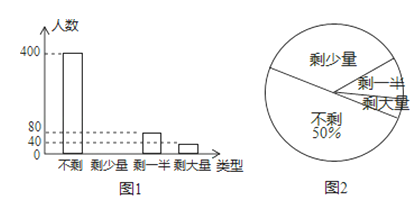(1)、被调查员工人数为人，并把条形统计图补充完整；

(2)、求扇形统计图中“剩一半”项目所对应扇形的圆心角度数；

(3)、若该企业有员工10000人，请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人？

查看试题解析
20. 如图，在 $△ A B C$ 中，以 $A C$ 为直径的 $⊙ O$ 交 $B C$ 于点D，交 $A B$ 于点M，点D是 $\overset{⌢}{C M}$ 的中点，连接 $A D$ ，点N为 $A C$ 延长线上的一点， $∠ B A C = 2 ∠ C D N$ ，

(1)、求证： $D N$ 是 $⊙ O$ 的切线；

(2)、若 $N D = 3 \sqrt{3} ， C N = 3$ ，求出 $\overset{⌢}{D M}$ 的长．

查看试题解析
21. 国家支持大学生创新办实业，提供小额无息贷款，学生王亮享受国家政策贷款36000元用于代理某品牌服装销售，已知该店代理的品牌服装的进价为每件40元，该品牌服装日销售量y（件）与销售价x（元/件）之间的关系可用图中的一条线段（实线）来表示．该店应支付员工的工资为每人每天82元，每天还应支付其它费用为106元（不包含贷款）．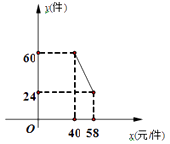

(1)、求日销售量y（件）与销售价x（元/件）之间的函数关系式；

(2)、若该店暂不考虑偿还贷款，当某天的销售价为48元/件时，当天正好收支平衡（销售额－成本=支出），求该店员工的人数；

(3)、若该店只有2名员工，则该店至少需要多少天能还清所有贷款？此时每件服装的价格应定为多少元？

查看试题解析
22. 如图， $A B$ 为 $⊙ O$ 直径， $C$ 是 $⊙ O$ 上一点， $C O ⊥ A B$ 于点 $O$ ，弦 $C D$ 与 $A B$ 交于点 $F$ .过点 $D$ 作 $⊙ O$ 的切线交 $A B$ 的延长线于点 $E$ ，过点 $A$ 作 $⊙ O$ 的切线交 $E D$ 的延长线于点 $G$ .

(1)、求证： $Δ E F D$ 为等腰三角形；

(2)、若 $O F ： O B = 1 ： 3$ ， $⊙ O$ 的半径为3，求 $A G$ 的长.

查看试题解析
23. 如图，抛物线y=ax²+bx+2经过点A(−1，0)，B(4，0)，交y轴于点C；

(1)、求抛物线的解析式(用一般式表示)；

(2)、点D为y轴右侧抛物线上一点，是否存在点D使S_△ABC= $\frac{2}{3}$ S_△ABD?若存在，请求出点D坐标；若不存在，请说明理由；

(3)、将直线BC绕点B顺时针旋转45°，与抛物线交于另一点E，求BE的长.

查看试题解析
24. 平行四边形 $A B C D$ 中，N为线段 $C D$ 上一动点.

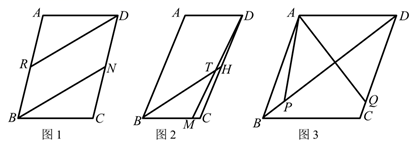(1)、如图1，已知 $∠ A D C < 90 °$ .若 $D R = B N$ ，求证：四边形 $D R B N$ 为平行四边形；

(2)、如图2，已知 $∠ A B C = 60 °$ .若 $B N$ 为 $∠ A B C$ 的角平分线，T为线段 $B N$ 上一点， $D T$ 的延长线交线段 $B C$ 于点M，满足： $\tan ∠ B T M = \frac{1}{2}$ 且 $D N = B M$ .请认真思考（1）中图形，探究 $\frac{M D}{A D}$ 的值.

(3)、如图3，平行四边形 $A B C D$ 中， $∠ A B C = 60 °$ ， $A B = B C = 2$ ，P在线段 $B D$ 上，Q在线段 $C D$ 上，满足： $B P = 2 C Q$ .直接写出 $(2 Q A + A P)$ 的最小值为.

查看试题解析