初中数学北师大版八年级下学期 第六章 6.3 三角形的中位线
试卷更新日期:2021-05-22 类型:同步测试
一、单选题
-
1. 如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )
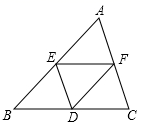 A、20 B、15 C、10 D、52. 如图,D、E分别是△ABC的边AB、AC的中点,若BC=6,则DE=( )
A、20 B、15 C、10 D、52. 如图,D、E分别是△ABC的边AB、AC的中点,若BC=6,则DE=( ) A、2 B、3 C、4 D、53. Rt△ABC两直角边的长分别为6cm和8cm,则连接这两条直角边中点的线段长为( )A、10cm B、3cm C、4cm D、5cm4. 如图,现有一等腰直角三角形 的腰长为4, ,将 沿 折叠,使 的顶点恰好落在 边的中点 处,则线段 的长度为( )
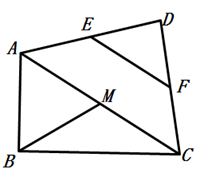
A、2 B、3 C、4 D、53. Rt△ABC两直角边的长分别为6cm和8cm,则连接这两条直角边中点的线段长为( )A、10cm B、3cm C、4cm D、5cm4. 如图,现有一等腰直角三角形 的腰长为4, ,将 沿 折叠,使 的顶点恰好落在 边的中点 处,则线段 的长度为( ) A、 B、 C、 D、5. 如图,M、N分别是△ABC的边AB、AC的中点,若∠A=65°,∠ANM=45°,则∠B=( )
A、 B、 C、 D、5. 如图,M、N分别是△ABC的边AB、AC的中点,若∠A=65°,∠ANM=45°,则∠B=( ) A、20° B、45° C、65° D、70°6. 如图,已知在Rt△ABC中,∠ACB=90°,∠A=30°, ;将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( ).
A、20° B、45° C、65° D、70°6. 如图,已知在Rt△ABC中,∠ACB=90°,∠A=30°, ;将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( ).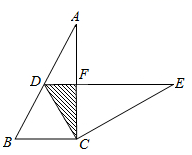 A、30,2 B、60,2 C、60, D、60,7. 如图,在Rt△ABC中,∠ACB=90°,AC=6,CD为中线,延长CB至点E,使BE=BC,连接DE,F为DE的中点,连接BF,若BF=3,则BC的长为( )
A、30,2 B、60,2 C、60, D、60,7. 如图,在Rt△ABC中,∠ACB=90°,AC=6,CD为中线,延长CB至点E,使BE=BC,连接DE,F为DE的中点,连接BF,若BF=3,则BC的长为( )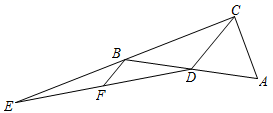 A、6 B、3 C、6 D、8
A、6 B、3 C、6 D、8二、填空题
-
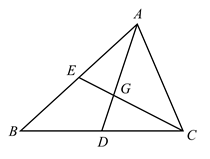
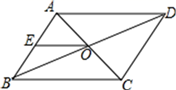
8. 如图,在平行四边形 中, 、 相交于点 ,点 是 的中点.若 ,则 的长是 .
 9. 如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么CD的长是
9. 如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么CD的长是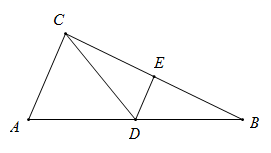 10. 如图,在 中, 分别是 的中点,连接 ,若 ,则四边形 的周长是.
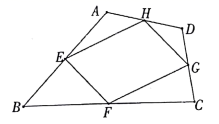
10. 如图,在 中, 分别是 的中点,连接 ,若 ,则四边形 的周长是.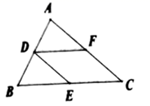 11. 已知三角形的周长为20cm,连接各边中点所得的三角形的周长为cm.12. 如图,任意四边形ABCD各边中点分别是E , F , G , H , 若对角线AC , BD的长都为10 cm , 则四边形EFGH的周长是cm .
11. 已知三角形的周长为20cm,连接各边中点所得的三角形的周长为cm.12. 如图,任意四边形ABCD各边中点分别是E , F , G , H , 若对角线AC , BD的长都为10 cm , 则四边形EFGH的周长是cm .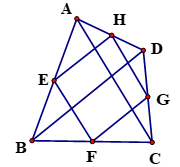 13. 如图,▱ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E,若OA=1,△AOE的周长等于5,则▱ABCD的周长等于.
13. 如图,▱ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E,若OA=1,△AOE的周长等于5,则▱ABCD的周长等于.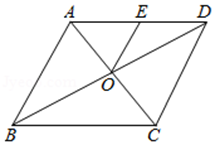 14. 如图,矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是BO、BC的中点,若AB=5,BC=12,则EF=;
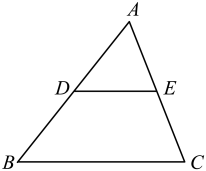
14. 如图,矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是BO、BC的中点,若AB=5,BC=12,则EF=; 15. 如图,D、E分别是△ABC的边AB和AC的中点,若BC=18,则DE= .
15. 如图,D、E分别是△ABC的边AB和AC的中点,若BC=18,则DE= .
三、解答题