浙江省备考2021年中考数学模拟试卷（绍兴市）

试卷更新日期：2021-05-22 类型：中考模拟

进入出卷网下载

一、选择题(本大题有10小题，每小题4分，共40分，)

1. 在 $\frac{1}{2}$ ，0，1，-9四个数中，负数是（）

A、 $\frac{1}{2}$ B、0 C、1 D、-9

查看试题解析
2. 某市大力发展新能源汽车生产，预计2019年的产量达51.7万辆，将51.7万用科学记数法表示为（）

A、 $5.17 \times 10^{3}$ B、 $5.17 \times 10^{4}$ C、 $5.17 \times 10^{5}$ D、 $5.17 \times 10^{6}$

查看试题解析
3. 图1和图2中所有的小正方形都全等，将图1的正方形放在图2中①、②、③、④的某个位置，使它与原来7个小正方形组成的图形是中心对称图形.这个位置是（）

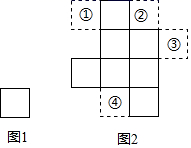A、① B、② C、③ D、④

查看试题解析
4. 如图，△ABC是⊙O的内接三角形，半径OB=3，sinA= $\frac{2}{3}$ ，则弦BC的长为（）

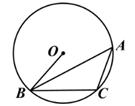A、3 B、4 C、5 D、3.75

查看试题解析
5. 如图，D、E是AB的三等分点，DF∥EG∥BC，图中三部分的面积分别为S₁ ， S₂ ， S₃ ，则S₁：S₂：S₃=（）

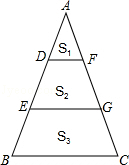A、1：2：3 B、1：2：4 C、1：3：5 D、2：3：4

查看试题解析
6. 将一枚飞镖投掷到如图所示的正六边形镖盘上，飞镖落在白色区域的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{2}{3}$

查看试题解析
7. 已知等腰三角形两边长分别是方程 $x^{2} - 6 x + 8 = 0$ 的两个根，则三角形周长为（）

A、6 B、8 C、10 D、8或10

查看试题解析
8. 如图，在四边形 $A B C D$ 中， $A D // B C$ ， $A D = 6$ ， $B C = 16$ ，E是 $B C$ 的中点．点P以每秒1个单位长度的速度从点A出发，沿 $A D$ 向点D运动；点Q同时以每秒3个单位长度的速度从点C出发，沿 $C B$ 向点B运动．点P停止运动时，点Q也随之停止运动．若以点 $P ， Q ， E ， D$ 为顶点的四边形是平行四边形，则点P运动的时间为（）

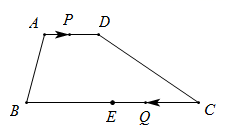A、1 B、 $\frac{7}{2}$ C、2或 $\frac{7}{2}$ D、1或 $\frac{7}{2}$

查看试题解析
9. 如图，在△ABC中，BD平分∠ABC，E是BC的中点，过点E作BC的垂线交BD于点F，连结CF。若∠A=50°，∠ACF=40°，则∠CFD的度数为（）

A、30° B、45° C、55° D、60°

查看试题解析
10. 同型号的甲、乙两辆车加满气体燃料后均可行驶210km，它们各自单独行驶并返回的最远距离是105km。现在它们都从A地出发，行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注人乙车的气体燃料桶，然后甲车再行驶返回A地，而乙车继续行驶，到B地后再行驶返回A地．则B地最远可距离A地（）

A、120km B、140km C、1 60km D、180km

查看试题解析

二、填空题(本大题有6小题，每小题5分，共30分)

11. 分解因式：x²﹣9= ．

查看试题解析
12. 已知 ${\begin{matrix} \end{matrix} \begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是关于x，y的二元一次方程组 ${\begin{matrix} \end{matrix} \begin{matrix} a x + b y = 7 \\ a x - b y = 1 \end{matrix}$ 的一组解，则a+b= ．

查看试题解析
13. 《九章算术》是我国古代重要的数学著作之一，在“勾股”中记载了一道“折竹抵地”问题：“今有竹高一丈，未折抵地，去本三尺，问折者高几何？”翻译成数学问题是：如图所示，△ABC中，∠ACB＝90°，AC+AB＝10，BC＝3，求AC的长，如果设AC＝x，则可列方程求出AC的长为.

查看试题解析
14. 在△ABC中，AB＝4，∠C＝60°，∠A＞∠B，则BC的长的取值范围是.

查看试题解析
15. 某公司生产一种饮料是由A，B两种原料液按一定比例配成，其中A原料液的原成本价为10元/千克，B原料液的原成本价为5元/千克，按原售价销售可以获得50%的利润率，由于物价上涨，现在A原料液每千克上涨20%，B原料液每千克上涨40%，配制后的饮料成本增加了 $\frac{1}{3}$ ，公司为了拓展市场，打算再投入现在成本的25%做广告宣传，如果要保证该种饮料的利润率不变，则这种饮料现在的售价应比原来的售价高元/千克.

查看试题解析
16. 如图，在平面直角坐标系中，矩形OABC的顶点A、C的坐标分别为（10，0），（0，4），点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为．

查看试题解析

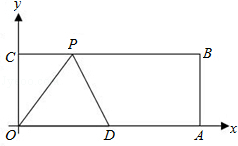
三、解答题(本大题有8小题，第17~20小题每小题8分，第21小题10分，第22，23小题每小题12分，第24小题14分，共80分.)

17.

(1)、计算：2^﹣¹+（2018﹣π）⁰﹣sin30°；

(2)、化简：（a+1）²﹣a（a+1）﹣1．

查看试题解析
18. 如图，在正方形ABCD中，点E（与点B、C不重合）是BC边上一点，将线段EA绕点E顺时针旋转90°到EF，过点F作BC的垂线交BC的延长线于点G，连接CF．

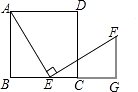(1)、求证：△ABE≌△EGF；

(2)、若AB=2，S_△_ABE=2S_△_ECF ，求BE．

查看试题解析

19. 前苏联教育家苏霍姆林斯曾说过：“让学生变聪明的方法，不是补课，不是増加作业量，而是阅读，阅读，再阅读”.课外阅读也可以促进我们养成终身学习的习惯.云南某学校组织学生利用课余时间多读书，读好书，一段时间后，学校对部分学生每周阅读时间进行调查，并绘制了不完整的频数分布表和频数分布直方图，如图所示：

时间（时）	频数	百分比
$0 \leq x < 3$	10	10%
$3 \leq x < 6$	25	m
$6 \leq x < 9$	n	30%
$9 \leq x < 12$	a	20%
$12 \leq x < 15$	15	15%

根据图表提供的信息，回答下列问题：

(1)、填空：m= ， n=；

(2)、请补全频数分布直方图；

(3)、该校共有3600名学生，估计学生每周阅读时间x（时）在

6 \leq x < 12

范围内的人数有多少人？

查看试题解析

20. 在抗击新型冠状病毒感染的肺炎疫情过程中，某医药研究所正在试研发一种抑制新型冠状病毒的药物，据临床观察：如果成人按规定的剂量注射这种药物，注射药物后每毫升血液中的含药量y（微克）与时间t（小时）之间的关系近似地满足图中折线.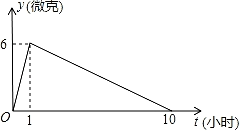

(1)、求注射药物后每毫升血液中含药量y与时间t之间的函数关系式，并写出自变量的取值范围；

(2)、据临床观察：每毫升血液中含药量不少于4微克时，对控制病情是有效的.如果病人按规定的剂量注射该药物后，求控制病情的有效时间.

查看试题解析
21. “三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图1所示的“三等分角仪”能三等分任一角.其抽象示意图如图2所示，由两根有槽的棒 $O A$ ， $O B$ 组成，两根棒在O点相连并可绕O转动.C点固定， $O C = C D = D E = 5 cm$ ，点D，E可在槽中滑动，

(1)、求证： $∠ B D E = 3 ∠ B O E$ .

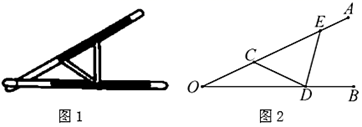(2)、若 $O D = 8 cm$ ，
①求 $∠ B D E$ 的度数；

②求点D到 $O A$ 的距离.

（参考数据： $\sin 36 ° \approx 0.60$ ， $\cos 36 ° \approx 0.80$ ， $\tan 36 ° \approx 0.75$ ， $\sin 66 ° \approx 0.92$ ， $\cos 66 ° \approx 0.40$ ， $\tan 66 ° \approx 2.24$ ）

查看试题解析
22. 在△ABC中，∠ACB＝90°，AC＝BC＝2，D是射线BC上一动点，过点B作BE⊥AD，垂足为点E，交直线AC于点P.

(1)、（问题发现）
如图①，若点D在BC的延长线上，试猜想AP，CD，BC之间的数量关系为；

(2)、（类比探究）
如图②，若点D在线段BC上，试猜想AP，CD，BC之间的数量关系，并说明理由；

(3)、（拓展应用）
当E为BP的中点时，直接写出线段CD的长度.

查看试题解析
23. 女生排球考试要求：垫球后，球在运动中离地面的最大高度至少为2米.某次模拟测试中，某女生在O处将球垫偏，之后又在A， B两处先后垫球，球沿抛物线C₁ → C₂ → C₃运动（假设抛物线C₁ ， C₂ ， C₃在同一平面内），最终正好在O处垫住，O处离地面的距离为1米.如图所示，以O为坐标原点1米为单位长度建立直角坐标系，x轴平行于地面水平直线m，已知点A（ $\frac{3}{2}$ ， $\frac{3}{8}$ ），点B的横坐标为 - $\frac{3}{2}$ ，抛物线C₁和C₃的表达式分别为 y = ax²- 2ax 和 y = 2ax² + bx （a≠ 0）.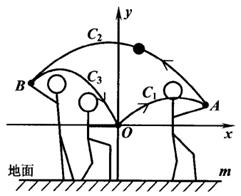

(1)、求抛物线C₁的函数表达式.

(2)、第一次垫球后，球在运动中离地面的最大高度是否达到要求？请说明理由.

(3)、为了使第三次垫球后，球在运动中离地面的最大高度达到要求，该女生第三次垫球处B 离地面的高度至少为多少米？

查看试题解析
24. 已知 $R t △ A B C$ 和 $R t △ D E B$ 中， $∠ A C B = ∠ D E B = 90 °$ ， $∠ A B C = ∠ D B E$ ， $D E = k A C$ （其中 $0 < k < 1$ ），连接AD、CE，点M为线段AD的中点，连接ME、MC， $△ B D E$ 绕点B顺时针旋转，探究线段ME与MC的数量关系．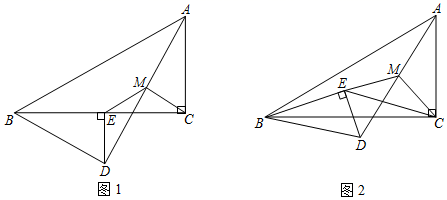

(1)、如图1，点E落在BC边上时，探究ME与MC的数量关系，并说明理由；

(2)、如图2，点E落在 $△ A B C$ 内部时，探究ME与MC的数量关系，并说明理由；

(3)、若 $∠ A B C = 30 °$ ， $k = \frac{\sqrt{3}}{3}$ ，当A、E、D共线时，直接写出 $\frac{C E}{B E}$ 的值．

查看试题解析