浙江省备考2021年中考数学模拟试卷（湖州市）

试卷更新日期：2021-05-22 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. $\sqrt{4}$ 的算术平方根是（）

A、2 B、±2 C、± $\sqrt{2}$ D、 $\sqrt{2}$

查看试题解析
2. 大树的价值很多，可以吸收有毒气体，防止大气污染，增加土壤肥力，涵养水源，为鸟类及其他动物提供繁衍场所等价值，累计计算，一棵50年树龄的大树总计创造价值超过160万元，其中160万元用科学记数法表示为（）

A、1.6×10⁵ B、1.6×10⁶ C、1.6×10⁷ D、1.6×10⁸

查看试题解析
3. 一个几何体的三视图如图所示，则这个几何体是（）

A、圆柱 B、三棱锥 C、球 D、圆锥

查看试题解析
4. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ， $F$ 是 $\overset{⌢}{C D}$ 上一点，且 $\overset{⌢}{D F} = \overset{⌢}{B C}$ ，连接 $C F$ 并延长交 $A D$ 的延长线于点 $E$ ，连接 $A C$ ，若 $∠ A B C = 105 °$ ， $∠ B A C = 25 °$ ，则 $∠ E$ 的度数为（）

A、 $60 °$ B、 $45 °$ C、 $50 °$ D、 $30 °$

查看试题解析
5. 一组数据4，4，5，5，x，6，7的平均数是5，则这组数据的众数和中位数分别是（）

A、4，5 B、4，4 C、5，4 D、5，5

查看试题解析
6. 若一次函数y＝kx+b图象经过第一、三、四象限，则关于x的方程x²﹣2x+kb+1＝0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、只有一个实数根

查看试题解析
7. 如图，在菱形 $ABCD$ 中，点 $E$ 是 $BC$ 的中点，以C为圆心、 $CE$ 为半径作弧，交 $CD$ 于点F，连接 $AE ， AF$ .若 $AB = 6$ ， $∠ B = 60^{\circ}$ ，则阴影部分的面积为（）

A、 $9 \sqrt{3} - 3 π$ B、 $9 \sqrt{3} - 2 π$ C、 $\frac{3}{2}$ D、 $18 \sqrt{3} - 6 π$

查看试题解析
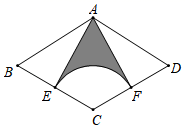8. 直线y=－2x+m与直线y=2x－1的交点在第四象限，则m的取值范围是（）

A、m＞－1 B、m＜1 C、－1＜m＜1 D、－1≤m≤1

查看试题解析
9. 如图，直线l₁∥l₂ ， ⊙O与l₁和l₂分别相切于点A和点B，点M和点N分别是l₁和l₂上的动点，MN沿l₁和l₂平移，若⊙O的半径为1，∠1=60°，下列结论错误的是（）

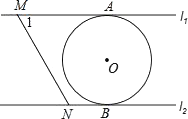A、MN= $\frac{4 \sqrt{3}}{3}$ B、若MN与⊙O相切，则AM= $\sqrt{3}$ C、l₁和l₂的距离为2 D、若∠MON=90°，则MN与⊙O相切

查看试题解析
10. 如图，小靓用七巧板拼成一幅装饰图，放入长方形ABCD内，装饰图中的三角形顶点E，F分别在边AB，BC上，△GHD的边GD在边AD上，则 $\frac{A B}{B C}$ 的值为（　　）

A、 $\frac{1 + \sqrt{2}}{4}$ B、4 $\sqrt{2}$ ﹣4 C、 $\frac{3 \sqrt{2} + 1}{3}$ D、 $\frac{9 \sqrt{2} + 3}{19}$

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 计算 $- 3 - 2 =$ ．

查看试题解析
12. 已知 $\frac{1}{a} + \frac{1}{b} = 2$ ，则 $\frac{a + b}{a - a b + b}$ ＝.

查看试题解析
13. 如图，AB为⊙O的直径，弦CD⊥AB于点E，已知CD=6，EB=1，则⊙O的半径为．

查看试题解析
14. 如图，电路图上有四个开关A、B、C、D和一个小灯泡，在开关全部断开的情况下，闭合其中任意一个开关，灯泡发亮的概率是；若闭合其中任意两个开关，灯泡发亮的概率是.

查看试题解析
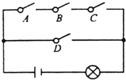15. 如图，已知M是平行四边形ABCD中AB边的三等分点，BD与CM交于E，则阴影部分面积与平行四边形面积比为.

查看试题解析
16. 如图，反比例函数y= $\frac{k}{x}$ （x＞0）的图象交Rt△OAB的斜边OA于点D，交直角边AB于点C，点B在x轴上．若△OAC的面积为5，AD：OD=1：2，则k的值为．

查看试题解析

三、解答题（本题有8小题，共66分）

17. 计算： $| 1 - \sqrt{3} | + {(\frac{1}{2})}^{- 1} - 1 - 2 \tan 60 °$ .

查看试题解析
18. 解不等式组 ${\begin{array}{l} \frac{x - 1}{2} \leq 1 \\ - 3 x - 5 \leq 1 \end{array}$ 并在数轴上画出不等式组的解集．

查看试题解析
19. 图1是一种折叠门，由上下轨道和两扇长宽相等的活页门组成，整个活页门的右轴固定在门框上，通过推动左侧活页门开关。图2是其俯视简化示意图，已知轨道AB=120cm，两扇活页门的宽OC=OB=60cm，点B固定，当点C在AB上左右运动时，OC与OB的长度不变。

(1)、若∠OBC=53°，求AC的长。
(结果保留整数，参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3)

(2)、当点C从点A向右运动60cm时，求点O在此过程中运动的路径长。

查看试题解析
20. 校体育组为了解全校学生“最喜欢的一项球类项目”，随机抽取了部分学生进行调查，下面是根据调查结果绘制的不完整的统计图：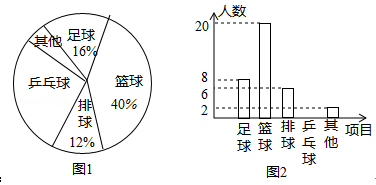

请你根据统计图回答下列问题：

(1)、喜欢乒乓球的学生所占的百分比是多少？并请补全条形统计图；

(2)、请你估计全校500名学生中最喜欢“排球”项目的有多少名？

(3)、在扇形统计图中，“篮球”部分所对应的圆心角是多少度？

(4)、篮球教练在制定训练计划前，将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈，请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.

查看试题解析
21. 如图，OA，OD是⊙O半径．过A作⊙O的切线，交∠AOD的平分线于点C，连接CD，延长AO交⊙O于点E，交CD的延长线于点B．

(1)、求证：直线CD是⊙O的切线；

(2)、如果D点是BC的中点，⊙O的半径为 3cm，求 $\vec{D E}$ 的长度．(结果保留π)

查看试题解析
22. 某旅行团32人在景区A游玩，他们由成人、少年和儿童组成．已知儿童10人，成人比少年多12人．

(1)、求该旅行团中成人与少年分别是多少人?

(2)、因时间充裕，该团准备让成人和少年（至少各1名）带领10名儿童去另一景区B游玩．景区B的门票价格为100元/张，成人全票，少年8折，儿童6折，一名成人可以免费携带一名儿童．①若由成人8人和少年5人带队，则所需门票的总费用是多少元?②若剩余经费只有1200元可用于购票，在不超额的前提下，最多可以安排成人和少年共多少人带队?求所有满足条件的方案，并指出哪种方案购票费用最少．

查看试题解析
23. 【概念认识】
定义：对角线互相垂直且相等的四边形叫做垂等四边形．

(1)、如图 1，已知在垂等四边形 ABCD 中，对角线 AC 与 BD 交于点 E ，若 AB⊥AD ， AB＝4cm，cos∠ABD= $\frac{4}{5}$ 求 AC 的长度，

(2)、【数学理解】
在探究如何画“圆内接垂等四边形”的活动中，小李与同学讨论出了如下方法：如图 2，在⊙O 中，已知 AB 是⊙O 的弦，只需作 OD⊥OA、OC⊥OB ，分别交⊙O 于点 D 和点 C ，即可得到垂等四边形 ABCD ，请你写出证明过程．

(3)、【问题解决】
如图 3，已知 A 是⊙O 上一定点，B 为⊙O 上一动点，以 AB 为一边作出⊙O 的内接垂等四边形(A、B 不重合且 A、B、0 三点不共线)，对角线 AC 与 BD 交于点 E ， ⊙O 的半径为 2 $\sqrt{2}$ ，当点 E 到 AD 的距离为 $\sqrt{3}$ 时，求弦 AB 的长度．

查看试题解析
24. 如图，已知A（-1，0），一次函数 $y = - \frac{1}{2} x + 2$ 的图象交坐标轴于点B、C，二次函数 $y = a x^{2} + b x + 2$ 的图象经过点A、C、B.点Q是二次函数图象上一动点。

(1)、当 $S_{△ Q A B} = 5 S_{△ A O C}$ 时，求点Q的坐标；

(2)、过点Q作直线 $l$ //BC，当直线 $l$ 与二次函数的图象有且只有一个公共点时，求出此时直线 $l$ 对应的一次函数的表达式并求出此时直线 $l$ 与直线BC之间的距离。

查看试题解析