浙江省备考2021年中考数学模拟试卷（宁波市）

试卷更新日期：2021-05-22 类型：中考模拟

进入出卷网下载

一、选择题(每小题4分，共40分)

1. 2的相反数是（）

A、 $\frac{1}{2}$ B、-2 C、 $\sqrt{2}$ D、 $\pm 2$

查看试题解析
2. 下列计算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $a^{2} \cdot a^{3} = a^{5}$ C、 ${(a^{2})}^{3} = a^{8}$ D、 ${(a b)}^{2} = a b^{2}$

查看试题解析
3. 在这次抗击新冠疫情的斗争中，全国共有13000多名90后医护驰援湖北.习近平主席在给北京大学援鄂医疗队全体“90后”党员的信中写到：“广大青年用行动证明，新时代的中国青年是好样的，是堪当大任的！”将13000用科学记数法表示应为（）

A、 $1.3 \times 10^{3}$ B、 $1.3 \times 10^{4}$ C、 $13 \times 10^{3}$ D、 $0.13 \times 10^{5}$

查看试题解析
4. 如图是小强用八块相同的小正方体积木搭建的几何体，这个几何体的主观图是（）

A、 B、 C、 D、

查看试题解析
5. 在一个不透明的袋子里装有红球，黄球共36个，这些球除颜色外都相同.小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能（）

A、5 B、9 C、15 D、24

查看试题解析
6. 函数y＝ $\frac{\sqrt{2 x - 1}}{x - 1}$ 中，自变量x的取值范围是（　　）

A、x $\leq \frac{1}{2}$ 且x≠1 B、x $\geq \frac{1}{2}$ 且x≠1 C、x $> \frac{1}{2}$ 且x≠1 D、x $< \frac{1}{2}$ 且x≠1

查看试题解析
7. 如图在菱形ABCD中，对角线AC、BD相交于点O，H为AD边中点，菱形ABCD的周长为32，则AH的长等于（）

A、8 B、6 C、7 D、4

查看试题解析
8. 《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十三两，问金、银各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚黄金重量相同），称重两袋相等，两袋互相交换1枚后，甲袋比乙袋轻了13辆（袋子重量忽略不计），问黄金、白银每枚各重多少两？设每枚黄金重x辆，每枚白银重y辆，根据题意得（）

A、 ${\begin{cases} 11 x = 9 y \\ (10 y + x) - (8 x + y) = 13 \end{cases}$ B、 ${\begin{cases} 10 y + x = 8 x + y \\ 9 x + 13 = 11 y \end{cases}$ C、 ${\begin{cases} 9 x = 11 y \\ (8 x + y) - (10 y + x) = 13 \end{cases}$ D、 ${\begin{cases} 9 x = 11 y \\ (10 y + x) - (8 x + y) = 13 \end{cases}$

查看试题解析
9. 抛物线y＝ax²+bx+c的顶点为(﹣1，3)，与x轴的交点A在点(﹣3，0)和(﹣2，0)之间，其部分图象如图，则以下结论，其中符合题意结论的个数为（）
①若点P(﹣3，m)，Q(3，n)在抛物线上，则m＜n；②c＝a+3；③a+b+c＜0；④方程ax²+bx+c＝3有两个相等的实数根．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，在平面直角坐标系中，O为坐标原点，将等边△ABC放在第一象限，其中边BC的端点B、C分别在x轴的正半轴、y轴的正半轴上滑动，D是AC的中点，AB=4，连接OD，则线段OD长度的最大值是（）

A、2 $\sqrt{3}$ B、4 C、2 $\sqrt{5}$ D、2 $\sqrt{6}$

查看试题解析

二、填空题(每小题5分，共30分)

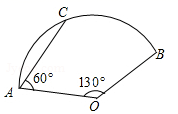
11. 若x,y为实数，且 $| x - 2 | + {(y + 4)}^{2} = 0,$ 则xy的立方根为。

查看试题解析
12. 分解因式：m²n - n³＝.

查看试题解析
13. 甲，乙两人进行飞镖比赛，每人各投6次.甲的成绩(单位:环)为:9，8，9.6，10，6.甲、乙两人平均成绩相等，乙成绩的方差为4.那么成绩较为稳定的是.(填“甲”或“乙“).

查看试题解析
14. 如图，在扇形AOB中，AC为弦，∠AOB=130°，∠CAO=60°，OA=6，则 $\overset{⌢}{B C}$ 的长为．

查看试题解析
15. 如图，在Rt△ABC中，∠C=90°，过点C作△ABC外接圆⊙O的切线交AB的垂直平分线于点D，AB的垂直平分线交AC于点E，若OE=2，AB=8，则CD=。

查看试题解析
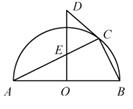16. 如图，函数 $y = \frac{k}{x}$ (k为常数，k＞0)的图象与过原点的O的直线相交于A ， B两点，点M是第一象限内双曲线上的动点（点M在点A的左侧），直线AM分别交x轴，y轴于C ， D两点，连接BM分别交x轴，y轴于点E ， F ．现有以下四个结论：①△ODM与△OCA的面积相等；②若BM⊥AM于点M ，则∠MBA＝30°；③若M点的横坐标为1，△OAM为等边三角形，则 $k = 2 + \sqrt{3}$ ；④若 $M F = \frac{2}{5} M B$ ，则MD＝2MA ．其中正确的结论的序号是．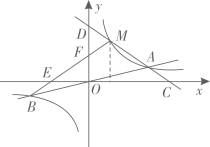

查看试题解析

三、解答题(本大题有8小题，共80分)

17.

(1)、计算 ${(- 2015)}^{0} + | 1 - \sqrt{2} | -$ $2 \cos 45 ° + \sqrt{8} + {(- \frac{1}{3})}^{- 2}$

(2)、解不等式 $\frac{3 x + 1}{2} \geq x$ .

查看试题解析
18. 如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．

(1)、请画出△ABC绕点O逆时针旋转90°得到的△A₁B₁C₁；

(2)、请画出△ABC以点O为对称中心的中心对称图形△A₂B₂C₂；

(3)、在x轴上求作一点P ，使△PAB的周长最小，请画出△PAB ，并直接写出点P的坐标．

查看试题解析
19. 如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交AC，BC于点D，E，过点B作⊙O的切线，交AC的延长线于点F.

(1)、求证：∠CBF= $\frac{1}{2}$ ∠CAB；

(2)、若CD=2， $\tan ∠ C B F = \frac{1}{2}$ ，求FC的长.

查看试题解析
20. 已知抛物线 $L_{1}$ ：y＝ $x^{2} + b x + c$ 经过点M（2，﹣3），与y轴交于点C（0，﹣3）.

(1)、求抛物线 $L_{1}$ 的表达式；

(2)、平移抛物线 $L_{1}$ ，设平移后的抛物线为 $L_{2}$ ，抛物线 $L_{2}$ 的顶点记为P，它的对称轴与x轴交于点Q，已知点N（2，﹣8），怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形？

查看试题解析

21. 某校为了了解全校学生线上学习情况，随机选取该校部分学生，调查学生居家学习时每天学习时间（包括线上听课及完成作业时间）．以下是根据调查结果绘制的统计图表．请你根据图表中的信息完成下列问题：

频数分布表

学习时间分组	频数	频率
A组（ $0 \leq x < 1$ ）	9	m
B组（ $1 \leq x < 2$ ）	18	0.3
C组（ $2 \leq x < 3$ ）	18	0.3
D组（ $3 \leq x < 4$ ）	n	0.2
E组（ $4 \leq x < 5$ ）	3	0.05

(1)、频数分布表中

m =

，

n =

，并将频数分布直方图补充完整；

(2)、若该校有学生1000名，现要对每天学习时间低于2小时的学生进行提醒，根据调查结果，估计全校需要提醒的学生有多少名？

(3)、已知调查的E组学生中有2名男生1名女生，老师随机从中选取2名学生进一步了解学生居家学习情况．请用树状图或列表求所选2名学生恰为一男生一女生的概率．

查看试题解析

22. 轿车从甲地出发匀速驶向乙地，到达乙地后，立即按原路原速返回甲地；货车从乙地出发沿相同路线匀速驶向甲地，出发t(t>0)小时后，货车因故障在途中停车1小时，然后继续按原速驶向甲地，货车在行驶过程中的速度是80千米/时，轿车比货车早1小时到达甲地，两车距各自出发地的路程y千米与轿车行驶时间 x小时之间的函数关系如图所示，请结合图象信息解答下列问题：

(1)、写出轿车行驶的速度，并直接写出图中（）内正确的数。

(2)、求轿车从乙地返回甲地的过程中，y与x的函数解析式(不需要写出自变量x的取值范围).

(3)、若轿车返回甲地后，立即按原路原速返回乙地，再经过多久，两车相遇。

查看试题解析
23. 天府新区某校数学活动小组在一次活动中，对一个数学问题作如下探究：

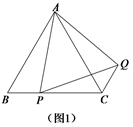
(1)、问题发现：如图1，在等边△ABC中，点P是边BC上任意一点，连接AP，以AP为边作等边△APQ，连接CQ.求证：BP = CQ；

(2)、变式探究：如图2，在等腰△ABC中，AB=BC，点P是边BC上任意一点，以AP为腰作等腰△APQ，使AP =PQ，∠APQ =∠ABC，连接CQ.判断∠ABC和∠ACQ的数量关系，并说明理由；

(3)、解决问题：如图3，在正方形ADBC中，点P是边BC上一点，以AP为边作正方形 APEF，Q是正方形APEF的中心，连接CQ.若正方形APEF的边长为6， $C Q = 2 \sqrt{2}$ ，求正方形ADBC的边长.

查看试题解析
24. 定义：有一组对角互余的四边形叫做对余四边形.

(1)、理解：若四边形 $A B C D$ 是对余四边形，则 $∠ A$ 与 $∠ C$ 的度数之和为；

(2)、证明：如图1， $M N$ 是 $⊙ O$ 的直径，点 $A ， B ， C$ 在 $⊙ O$ 上， $A M$ ， $C N$ 相交于点D.
求证：四边形 $A B C D$ 是对余四边形；

(3)、探究：如图2，在对余四边形 $A B C D$ 中， $A B = B C$ ， $∠ A B C = 60^{°}$ ，探究线段 $A D$ ， $C D$ 和 $B D$ 之间有怎样的数量关系？写出猜想，并说明理由.

查看试题解析