浙江省备考2021年中考数学模拟试卷(衢州市)
试卷更新日期:2021-05-22 类型:中考模拟
一、选择题(本题共有10小题,每小题3分,共30分)
-
1. 比﹣2小1的数是( )A、2 B、0 C、﹣1 D、﹣32. 下列几何体中,主视图与俯视图不相同的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算中,正确的是( )A、a2·a3=a6 B、a3÷a-3=1 C、(a-b)2=a2-ab+b2 D、(-a2)3=-a64. 正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为( )
3. 下列计算中,正确的是( )A、a2·a3=a6 B、a3÷a-3=1 C、(a-b)2=a2-ab+b2 D、(-a2)3=-a64. 正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为( )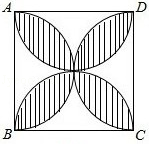 A、 B、 C、 D、5. 下列二次根式中,无论x取什么值都有意义的是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上用阴影表示正确的是( )A、
A、 B、 C、 D、5. 下列二次根式中,无论x取什么值都有意义的是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上用阴影表示正确的是( )A、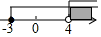 B、
B、 C、
C、 D、
D、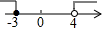 7. 为执行“均衡教育"政策,某县2017年投入教育经费 万元,预计到2019年底三年累计投入 亿元.若每年投人教育经费的年平均增长百分率为x,则下列方程正确的是( )A、 B、 C、 D、8. 在以下三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是( )
7. 为执行“均衡教育"政策,某县2017年投入教育经费 万元,预计到2019年底三年累计投入 亿元.若每年投人教育经费的年平均增长百分率为x,则下列方程正确的是( )A、 B、 C、 D、8. 在以下三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是( )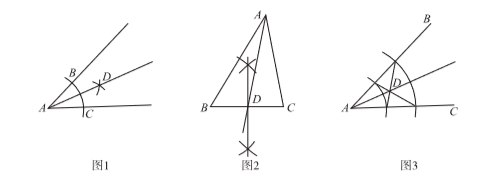 A、图2 B、图1与图2 C、图1与图3 D、图2与图39. 在平面直角坐标系中,抛物线y=(x﹣5)(x+3)经平移变换后得到抛物线y=(x﹣3)(x+5),则这个变换可以是( )A、向左平移2个单位长度 B、向右平移2个单位长度 C、向左平移8个单位长度 D、向右平移8个单位长度10. 如图,在正方形 中, 为对角线,点E在 边上, 于点F , 连接 的周长为12,则EB的长为( )
A、图2 B、图1与图2 C、图1与图3 D、图2与图39. 在平面直角坐标系中,抛物线y=(x﹣5)(x+3)经平移变换后得到抛物线y=(x﹣3)(x+5),则这个变换可以是( )A、向左平移2个单位长度 B、向右平移2个单位长度 C、向左平移8个单位长度 D、向右平移8个单位长度10. 如图,在正方形 中, 为对角线,点E在 边上, 于点F , 连接 的周长为12,则EB的长为( )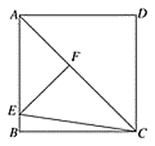 A、 B、 C、 D、5
A、 B、 C、 D、5二、填空题(本题共有6小题,每小题4分,共24分)
-
11. 关于x的一元一次方程 的解为x=1,则a+m的值为.
12. 如果y=x2-3,y=-x2+3,那么x4-y2= .13. 在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为.14. 七巧板是一种古老的中国传统智力游戏.小明利用七巧板(如图1)拼出了一个数字“7”(如图2),若图1中正方形ABCD的面积为32cm2 , 则图2的周长为cm 15. 如图,点A是反比例函数y= (x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB= .点C是反比例函数y= (x>0)图象上一动点,连接AC,OC,若△AOC的面积为 ,则点C的坐标为 .
15. 如图,点A是反比例函数y= (x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB= .点C是反比例函数y= (x>0)图象上一动点,连接AC,OC,若△AOC的面积为 ,则点C的坐标为 .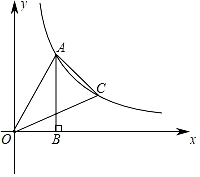 16. 如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为 ,则图中阴影部分的面积为.
16. 如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为 ,则图中阴影部分的面积为.
三、解答题(本题共有8小题,第17~19小题每小题6分,第20~21小题每小题8分,第22~23小题每小题10分,第24小题12分,共66分。请务必写出解答过程)
-
17. 计算: .18. 先化简,再求值: ,其中 .19. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
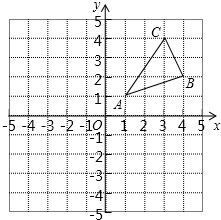 (1)、请画出△ABC关于原点对称的△A1B1C1;(2)、四边形CBC1B1为四边形;(3)、点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.20. 近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
(1)、请画出△ABC关于原点对称的△A1B1C1;(2)、四边形CBC1B1为四边形;(3)、点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.20. 近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,C类表示“听同学讲过”,D类表示“不知道”,划分类别后的数据整理如表:
类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06
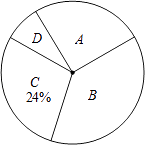 (1)、表中的a=b=;(2)、根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;(3)、若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?21. 如图,⊙O是等边△ACD的外接圆,AB是⊙O的直径,过点B作⊙O的切线BM,延长AD交BM于点E.
(1)、表中的a=b=;(2)、根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;(3)、若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?21. 如图,⊙O是等边△ACD的外接圆,AB是⊙O的直径,过点B作⊙O的切线BM,延长AD交BM于点E.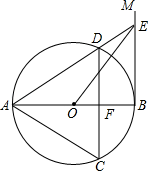 (1)、求证:CD∥BM;(2)、连接OE,若DE=4,求OE的长.22. 现有甲骑电瓶车,乙骑自行车从湖州西山漾公园丝绸小镇门口出发沿同一路线匀速前往太湖龙之梦乐园.设乙行驶的时间为x(h),甲、乙两人距出发点的路程S甲、S乙关于x的函数图象如图①所示;甲、乙两人之间的路程差y关于x的函数图象如图②所示:
(1)、求证:CD∥BM;(2)、连接OE,若DE=4,求OE的长.22. 现有甲骑电瓶车,乙骑自行车从湖州西山漾公园丝绸小镇门口出发沿同一路线匀速前往太湖龙之梦乐园.设乙行驶的时间为x(h),甲、乙两人距出发点的路程S甲、S乙关于x的函数图象如图①所示;甲、乙两人之间的路程差y关于x的函数图象如图②所示: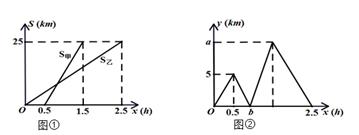
请你解决以下问题:
(1)、甲的速度是km/h;乙的速度是km/h ;(2)、对比图①、图②可知: a=;b=.(3)、乙出发多少时间,甲、乙两人路程差为7.5km?23. 如图,在矩形 中, , ,点 是对角线 上的一个动点,过点 作 ,交边 于点 (点 与点 , 都不重合),点 是射线 上一动点,连结 , ,并一直保持 .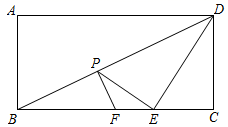 (1)、求证: .(2)、设 的长为 , 的面积为 ,求 关于 的函数表达式,并写出自变量 的取值范围.(3)、当 与 相似时,求 的面积.24. 定义:有两边之比为 的三角形叫做智慧三角形.(1)、如图1,在智慧三角形 中, 为 边上的中线,求 的值;
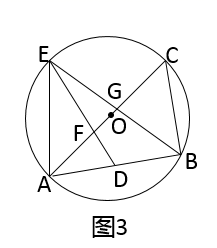
(1)、求证: .(2)、设 的长为 , 的面积为 ,求 关于 的函数表达式,并写出自变量 的取值范围.(3)、当 与 相似时,求 的面积.24. 定义:有两边之比为 的三角形叫做智慧三角形.(1)、如图1,在智慧三角形 中, 为 边上的中线,求 的值;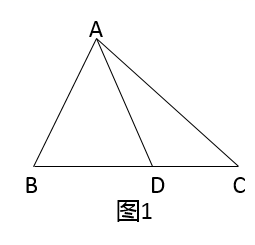 (2)、如图2, 是⊙O的内接三角形, 为直径,过 的中点D作 交线段 于点F,交⊙O于点E,连结 交 于点G.
(2)、如图2, 是⊙O的内接三角形, 为直径,过 的中点D作 交线段 于点F,交⊙O于点E,连结 交 于点G.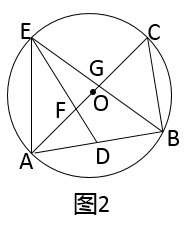
①求证: 是智慧三角形;
②设 ,若⊙O的半径为 ,求y关于x的函数表达式;
(3)、如图3,在(2)的条件下,当 时,求 的余弦值.