浙江省备考2021年中考数学模拟试卷（台州市）

试卷更新日期：2021-05-22 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题4分，共40分.请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）

1. 若（）﹣5＝﹣3，则括号内的数是（）

A、﹣2 B、﹣8 C、2 D、8

查看试题解析
2. 如图所示的几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、2a³•3a²＝6a⁶ B、（﹣a）³ⁿ÷（﹣a）²ⁿ＝aⁿ C、（a+b）³＝a³+b³ D、（﹣a³）⁴＝a¹²

查看试题解析
4. 最接近 $\sqrt{7}$ 的整数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 一组数据：1，3，3，5，若添加一个数据3，则下列统计量中发生变化的是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
6. 如图，将一颗小星星放置在平面直角坐标系中第二象限内的甲位置，先将它绕原点O旋转 $180 °$ 到乙位置，再将它向上平移 $2$ 个单位长到丙位置，则小星星顶点A在丙位置中的对应点 $A^{'}$ 的坐标为（）

A、 $(- 3 ， 1)$ B、 $(1 ， 3)$ C、 $(3 ， 1)$ D、 $(3 ， - 1)$

查看试题解析
7. 如图，四边形ABCD是平行四边形，以点A为圆心、AB的长为半径画弧交AD于点F，再分别以点B，F为圆心、大于 $\frac{1}{2}$ BF的长为半径画弧，两弧交于点M，作射线AM交BC于点E，连接EF.下列结论中不一定成立的是（）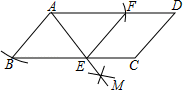

A、BE＝EF B、EF∥CD C、AE平分∠BEF D、AB＝AE

查看试题解析
8. 在平行四边形ABCD中，AC，BD是两条对角线，现从以下四个关系：①AB＝BC，②AC＝BD，③AC⊥BD，④AB⊥BC中任取一个作为条件，即可推出平行四边形ABCD是菱形的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
9. 如图，在边长为3的菱形ABCD中，点P从A点出发，沿A→B→C→D运动，速度为每秒3个单位；点Q同时从A点出发，沿A→D运动，速度为每秒1个单位，则 $Δ A P Q$ 的面积S关于时间 $t$ 的函数图象大致为（）

A、 B、 C、 D、

查看试题解析
10. 如图，在矩形ABCD中，∠ADC的平分线与AB交于E，点F在DE的延长线上，∠BFE=90°，连接AF、CF，CF与AB交于G．有以下结论：①AE=BC②AF=CF③BF²=FG•FC④EG•AE=BG•AB其中正确的个数是（）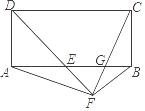

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本题有6小题，每小题5分，共30分）

11. 分解因式：a³﹣9a= ．

查看试题解析
12. 化简： $\frac{2 a}{a^{2} - b^{2}} + \frac{1}{b - a}$ 的结果是.

查看试题解析
13. 如图，l∥m，等腰直角三角形ABC的直角顶点C在直线m上，若∠β=35°，则∠α的度数为．

查看试题解析
14. 今年某果园随机从甲、乙、丙三个品种的枇杷树中各选了5棵，每棵产量的平均数 $\bar{x}$ (单位：千克)及方差 $S^{2}$ (单位：千克²)如下表所示：

甲

乙

丙

$\bar{x}$

45

45

42

$S^{2}$

1.8

2.3

1.8

明年准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植，则应选的品种.

查看试题解析
15. 如图，ABCD是⊙O的内接四边形，AB是⊙O的直径，过点D的切线交BA的延长线于点E，若∠ADE＝25°，则∠C＝度.

查看试题解析
16. 如图，在平面直角坐标系中，正方形 $A B C D$ 的对角线相交于点 $E ， A (2 ， 0) ， B (6 ， 0)$ ，将正方形 $A B C D$ 以 $A$ 为位似中心， $1 ： 2$ 为位似比缩小，点 $E$ 的对应点 $E^{'}$ 的坐标是

查看试题解析

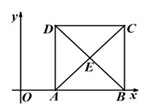
三、解答題（本题有8小题，第17~20题每题8分，第21题10分，第22,23题每题12分,第题14分，共80分）

17. 计算：（﹣2）²+|﹣ $\sqrt{3}$ |+2sin60°﹣ $\sqrt{12}$ ．

查看试题解析
18. 解方程组 ${\begin{array}{l} 3 x + 5 y = 50 \\ 2 x + 3 y = 31 \end{array}$

查看试题解析
19. 如图，要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角 $α$ 一般要满足 $50^{°} ⩽ α \leq 75^{°}$ ，现有一架长为 $6m$ 的梯子，当梯子底端离墙面 $2m$ 时，此时人是否能够安全使用这架梯子（参考数据： $\sin 50^{°} \approx 0.77 ， \cos 50^{°} \approx 0.64$ ， $\sin 75^{°} \approx 0.97 ， \cos 75^{°} = 0.26$ ）？

查看试题解析
20. 月电科技有限公司用160万元，作为新产品的研发费用，成功研制出了一种市场急需的电子产品，已于当年投入生产并进行销售．已知生产这种电子产品的成本为4元/件，在销售过程中发现：每年的年销售量y（万件）与销售价格x（元/件）的关系如图所示，其中AB为反比例函数图象的一部分，BC为一次函数图象的一部分．设公司销售这种电子产品的年利润为s（万元）．（注：若上一年盈利，则盈利不计入下一年的年利润；若上一年亏损，则亏损计作下一年的成本．）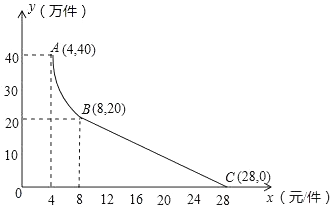

(1)、请求出y（万件）与x（元/件）之间的函数关系式；

(2)、求出第一年这种电子产品的年利润s（万元）与x（元/件）之间的函数关系式，并求出第一年年利润的最大值．

(3)、假设公司的这种电子产品第一年恰好按年利润s（万元）取得最大值时进行销售，现根据第一年的盈亏情况，决定第二年将这种电子产品每件的销售价格x（元）定在8元以上（x＞8），当第二年的年利润不低于103万元时，请结合年利润s（万元）与销售价格x（元/件）的函数示意图，求销售价格x（元/件）的取值范围．

查看试题解析
21. 如图，在▱ABCD中，点O是对角线AC的中点，直线EF分别交AD、BC于点E，F．连接CE，AF，

(1)、求证：△AOE≌△COF.

(2)、若EF⊥AC，猜想四边形AECF形状，并证明你的猜想.

查看试题解析

22. 重庆一中开展了“爱生活•爱运动”的活动，以鼓励学生积极参与体育锻炼.为了解学生每周体育锻炼时间，学校在活动之前对八年级同学进行了抽样调査，并根据调査结果将学生每周的体育锻炼时间分为3小时、4小时、5小时、6小时、7小时共五种情况.小明根据调查结构制作了如图两幅统计图，请你结合图中所给信息解答下列问题：

（整理数据）

“爱生活•爱运动”的活动结束之后，再次抽查这部分学生的体育锻炼时间：

一周体育锻炼时间（小时）	3	4	5	6	7
人数	3	5	15	a	10

活动之后部分学生体育锻炼时间的统计表

（分析数据）

	平均数	中位数	众数
活动之前锻炼时间（小时）	5	5	5
活动之后锻炼时间（小时）	5.52	b	c

请根据调查信息分析：

(1)、补全条形统计图，并计算a＝， b＝小时，c＝小时；

(2)、小亮同学在活动之前与活动之后的这两次调查中，体育锻炼时间均为5小时，根据体育锻炼时间由多到少进行排名统计，请问他在被调查同学中体育锻炼时间排名靠前的是（填“活动之前”或“活动之后”），理由是；

(3)、已知八年级共2200名学生，请估算全年级学生在活动结束后，每周体育锻炼时间至少有6小时的学生人数有多少人？

查看试题解析

23. 如图，在矩形 $A B C D$ 中， $A B = 4$ ， $B C = 8$ ，点P在边 $B C$ 上（点P与端点B、C不重合），以P为圆心， $P B$ 为半径作圆，圆P与射线 $B D$ 的另一个交点为点E，直线 $C E$ 与射线 $A D$ 交于点G．点M为线段 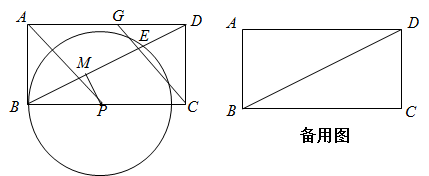$B E$ 的中点，联结 $P M$ ．设 $B P = x ， B M = y$ ．

(1)、求y关于x的函数解析式，并写出该函数的定义域；

(2)、联结 $A P$ ，当 $A P / / C E$ 时，求x的值；

(3)、如果射线 $E C$ 与圆P的另一个公共点为点F，当 $△ C P F$ 为直角三角形时，求 $△ C P F$ 的面积．

查看试题解析
24. 如图l，皮皮小朋友燃放-种手持烟花，这种烟花每隔1.4秒发射-发花弹，每-发花弹的飞行路径，爆炸时的高度均相同.皮皮小朋友发射出的第-发花弹的飞行高度h(米)随飞行时间t(秒)变化的规律如下表，

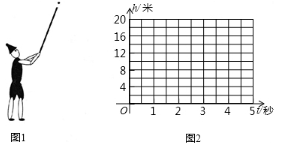
(1)、根据这些数据在图2的坐标系中画出相应的点，选择适当的函数表示h与t之间的关系，并求出相应的函数解析式；

(2)、当t=t_l时，第-发花弹飞行到最高点，此时高度为h_l.在t≠t₁的情况下，随着t的增大， $\frac{| h - h_{1} |}{| t - t_{1} |}$ 的变化趋势是（）

A、-直增大 B、-直减小 C、先增大后减小 D、先减小后增大

(3)、为了安全，要求花弹爆炸时的高度不低于l5米.皮皮发现在第-发花弹爆炸的同时，第三发花弹与它处于同-高度，请分析花弹的爆炸高度是否符合安全要求?

查看试题解析

	甲	乙	丙
$\bar{x}$	45	45	42
$S^{2}$	1.8	2.3	1.8