浙江省备考2021年中考数学模拟试卷(舟山市)
试卷更新日期:2021-05-22 类型:中考模拟
一、选择题(本题有10小题,每题3分,共30分)
-
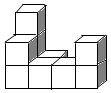
1. 近年来,我国5G发展取得明显成效,截至2020年2月底,全国建设开通5G基站达16.4万个,将数据16.4万用科学记数法表示为( )A、 B、 C、 D、2. 如图是由相同小正方体组成的立体图形,其俯视图为( )
 A、
A、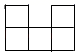 B、
B、 C、
C、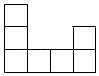 D、
D、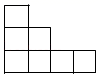 3. 某大桥某一周的日均车流量分别为13,14,11,10,12,12,15(单位:千辆),则这组数据的中位数与众数分别为( )A、10,12 B、12,10 C、12,12 D、13,124. 在同一平面直角坐标系中,函数 与 的图象可能是( )A、
3. 某大桥某一周的日均车流量分别为13,14,11,10,12,12,15(单位:千辆),则这组数据的中位数与众数分别为( )A、10,12 B、12,10 C、12,12 D、13,124. 在同一平面直角坐标系中,函数 与 的图象可能是( )A、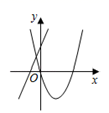 B、
B、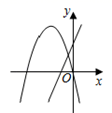 C、
C、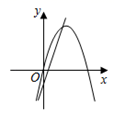 D、
D、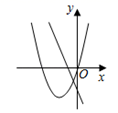 5. 如图,平面直角坐标系中,点E(﹣4,2),F(﹣1,﹣1),以原点O为位似中心,把△EFO缩小为△E′F′O , 且△E′F′O与△EFO的相似比为1:2,则点E的对应点E′的坐标为( )
5. 如图,平面直角坐标系中,点E(﹣4,2),F(﹣1,﹣1),以原点O为位似中心,把△EFO缩小为△E′F′O , 且△E′F′O与△EFO的相似比为1:2,则点E的对应点E′的坐标为( )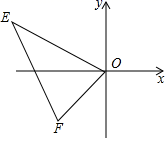 A、(2,﹣1) B、(8,﹣4) C、(2,﹣1)或(﹣2,1) D、(8,﹣4)或(﹣8,4)6. 不等式2x+3>1的解集在数轴上表示正确的是( )A、
A、(2,﹣1) B、(8,﹣4) C、(2,﹣1)或(﹣2,1) D、(8,﹣4)或(﹣8,4)6. 不等式2x+3>1的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、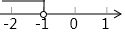 D、
D、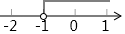 7. 如图,点O是边长为1的等边三角形 的中心,将 绕点O逆时针方向旋转 ,得到 ,则 与 重叠部分(图中阴影部分)的面积为( )
7. 如图,点O是边长为1的等边三角形 的中心,将 绕点O逆时针方向旋转 ,得到 ,则 与 重叠部分(图中阴影部分)的面积为( )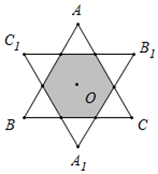 A、 B、 C、 D、8. 已知 关于的二元一次方程组 的解满足 ,且关于x的不等式组 无解,那么所有符合条件的整数a的个数为( )A、6个 B、7个 C、8个 D、9个9. 如图, 是 的直径, 切 于点 , ,点 在 上, 交 于 , ,则 的长是( )
A、 B、 C、 D、8. 已知 关于的二元一次方程组 的解满足 ,且关于x的不等式组 无解,那么所有符合条件的整数a的个数为( )A、6个 B、7个 C、8个 D、9个9. 如图, 是 的直径, 切 于点 , ,点 在 上, 交 于 , ,则 的长是( )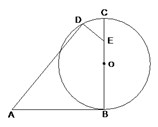 A、 B、 C、 D、10. 如图,在平面直角坐标系 中,函数 的图像与对称轴直线 交于点A,与 轴交于 三点,下列命题正确的是( )
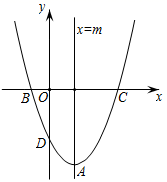
A、 B、 C、 D、10. 如图,在平面直角坐标系 中,函数 的图像与对称轴直线 交于点A,与 轴交于 三点,下列命题正确的是( )① ;②若 ,则 ;③对于任意 ,始终有 ;④若B的坐标为 ,则C的坐标为 .
 A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题(本题有6小题,每题4分,共24分)
-
11. 分解因式:x4﹣2x2y2+y4=.12. 如图,在四边形 中,对角线 交于点 ,且 ,若要使四边形 是菱形,则可以添加的条件是 .
 13. 小明和小红玩抛硬币游戏,连续抛两次,小明说:“如果两次都是正那赢;如 果两次是一正一反,则我嬴.”小红赢的概率是 ,据此判断该游戏 (填“公平”或“不公平”).14. 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为 的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为 cm2 .
13. 小明和小红玩抛硬币游戏,连续抛两次,小明说:“如果两次都是正那赢;如 果两次是一正一反,则我嬴.”小红赢的概率是 ,据此判断该游戏 (填“公平”或“不公平”).14. 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为 的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为 cm2 .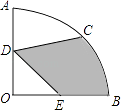 15. 新冠疫情期间,口罩成为了人们出行必备的防护工具.某药店抓住商机购进甲、乙、丙三种口罩进行销售.已知销售每件甲种口罩的利润率为30%,每件乙种口罩的利润率为20%,每件丙种口罩的利润率为5%.当售出的甲、乙、丙口罩件数之比为1:3:2时,药店得到的总利润率为20%;当售出的甲、乙、丙口罩件数之比为3:2:2时,药店得到的总利润率为24%.因丙种口罩利润较低,现药店准备只购进甲、乙两种口罩进行销售,若该药店想要获得的总利润率为28%,则该药店应购进甲、乙两种口罩的数量之比是.16. 如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE= ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为.
15. 新冠疫情期间,口罩成为了人们出行必备的防护工具.某药店抓住商机购进甲、乙、丙三种口罩进行销售.已知销售每件甲种口罩的利润率为30%,每件乙种口罩的利润率为20%,每件丙种口罩的利润率为5%.当售出的甲、乙、丙口罩件数之比为1:3:2时,药店得到的总利润率为20%;当售出的甲、乙、丙口罩件数之比为3:2:2时,药店得到的总利润率为24%.因丙种口罩利润较低,现药店准备只购进甲、乙两种口罩进行销售,若该药店想要获得的总利润率为28%,则该药店应购进甲、乙两种口罩的数量之比是.16. 如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE= ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为.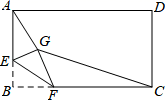
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
17. 计算:(1)、(2)、化简:18. 阅读下列材料:
( 1 )关于x的方程x2﹣3x+1=0(x≠0)方程两边同时乘以 得:x-3+ =0即x+ =3, , .
( 2 )a3+b3=(a+b)(a2﹣ab+b2);a3﹣b3=(a﹣b)(a2+ab+b2).
根据以上材料,解答下列问题:
(1)、x2﹣4x+1=0(x≠0),则x+ =1 , = , =;(2)、2x2﹣7x+2=0(x≠0),求 的值.19. 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.求证:AP=BP. 20. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y=
20. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y=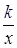 (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3). 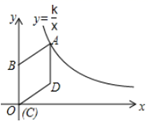 (1)、求k的值;(2)、若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=
(1)、求k的值;(2)、若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=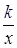 (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离. 21. 学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类:A:好,B:中,C:差.请根据图中信息,解答下列问题:
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离. 21. 学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类:A:好,B:中,C:差.请根据图中信息,解答下列问题: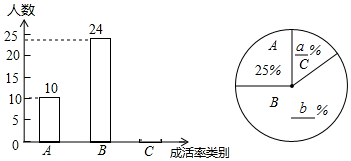 (1)、求全班学生总人数;(2)、在扇形统计图中,a= , b= , C类的圆心角为;(3)、张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请求出全是B类学生的概率.22. 如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)
(1)、求全班学生总人数;(2)、在扇形统计图中,a= , b= , C类的圆心角为;(3)、张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请求出全是B类学生的概率.22. 如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)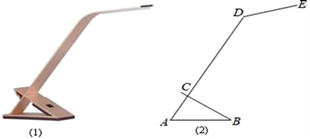 (1)、求DE与水平桌面(AB所在直线)所成的角;(2)、求台灯的高(点E到桌面的距离,结果精确到0.1cm).23. 如图,在菱形ABCD中,AB=AC,点E、F、G分别在边BC、CD上,BE=CG,AF平分∠EAG,点H是线段AF上一动点(与点A不重合).
(1)、求DE与水平桌面(AB所在直线)所成的角;(2)、求台灯的高(点E到桌面的距离,结果精确到0.1cm).23. 如图,在菱形ABCD中,AB=AC,点E、F、G分别在边BC、CD上,BE=CG,AF平分∠EAG,点H是线段AF上一动点(与点A不重合).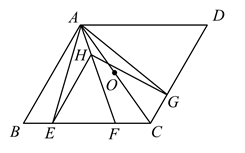 (1)、求证:△AEH≌△AGH;(2)、当AB=12,BE=4时:
(1)、求证:△AEH≌△AGH;(2)、当AB=12,BE=4时:①求△DGH周长的最小值;
②若点O是AC的中点,是否存在直线OH将△ACE分成三角形和四边形两部分,其中三角形的面积与四边形的面积比为1:3.若存在,请求出 的值;若不存在,请说明理由.
24. 如图,在平面直角坐标系xOy中,一次函数y= x+m(m为常数) 的图象与x轴交于点A(-3,0),与y轴交于点C,以直线x=1为对称轴的拋物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B。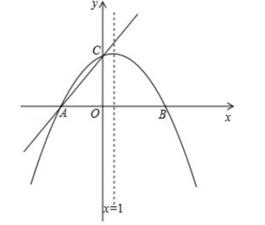
(参考公式:在平面直角坐标之中,若A((x1 , y1),B(x2 , y2),则A,B两点间的距离为AB= )
(1)、求m的值及抛物线的函数表达式;(2)、是否存在抛物线上一动点Q, 使得△ACQ是以AC为直角边的直角三角形?若存在, 求出点Q的横坐标;若存在,请说明理由;(3)、若P是抛物线对称轴上一动点, 且使△ACP周长最小, 过点P任意作一条与y轴不平行的直线交抛物线于M1 (x1 , y1),M2(x2;y2)两点,试问 是否为定值,如果是,请求出结果,如果不是请说明理由。