初中数学人教版八年级下学期第十九章单元巩固练习题

试卷更新日期：2021-05-21 类型：单元试卷

进入出卷网下载

一、单选题

1. 一次函数y＝－3x－2的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知，直线l经过第二、三、四象限，l的解析式是y=（m﹣2）x+n，则m的取值范围在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
3.
如图，直线y=kx+b与x轴交于点A（-4，0），则当y＜0时，x的取值范围是（）

A、x＞-4 B、x＞0 C、x＜-4 D、x＜0

查看试题解析
4. 函数y=（2m-1）x是正比例函数，且y随自变量x的增大而增大，则m的取值范围是（　　）

A、m> $\frac{1}{2}$ B、m< $\frac{1}{2}$ C、m≥ $\frac{1}{2}$ D、m≤ $\frac{1}{2}$

查看试题解析
5. 若一次函数 $y = k x + b$ 的图象不经过第二象限，则关于 $x$ 的方程 $x^{2} + k x + b = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
6. 在无锡全民健身越野赛中，甲、乙两选手的行程 y（千米）随时间（时）变化的图象（全程）如图所示．下列四种说法：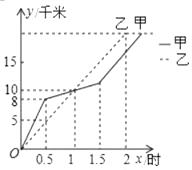
①起跑后 1 小时内，甲在乙的前面；
②第 1 小时两人都跑了 10 千米；
③甲比乙先到达终点；
④两人都跑了 20 千米．
正确的有（）

A、①②③④ B、①②③ C、①②④ D、②③④

查看试题解析
7. 如果实数k，b满足kb<0，且不等式kx<b的解集是x> $\frac{b}{k}$ ，那么函数y=kx+b的图象只可能是（）

A、 B、 C、 D、

查看试题解析
8. 小明家、食堂、图书馆依次在同一条直线上，小明从家去食堂吃早餐，接着去图书馆读报，然后回家．如图反映了这个过程，小明离家的距离与时间之间的对应关系，下列说法错误的是（）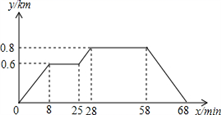

A、小明从家到食堂用了8min B、小明家离食堂0.6km，食堂离图书馆0.2km C、小明吃早餐用了30min，读报用了17min D、小明从图书馆回家的平均速度为0.08km/min

查看试题解析
9. 目前，全球淡水资源日益减少，提倡全社会节约用水。据测试：拧不紧的水龙头每分钟滴出100滴水，每滴水约0.05毫升。小康同学洗手后，没有把水龙头拧紧，水龙头以测试的速度滴水，当小康离开x分钟后，水龙头滴出y毫升的水，请写出y与x之间的函数关系式是（）

A、y=0.05x B、y=5x C、y=100x D、y=0.05x+100

查看试题解析
10. 如果一次函数y=kx+b，当-3≤x≤1时，-1≤y≤7，则kb的值为（）

A、10 B、21 C、－10或2 D、－2或10

查看试题解析
11. 如图，已知一次函数 $y=k x+b$ 的图象与x轴，y轴分别交于点（2，0），点（0，3）．有下列结论：①关于x的方程 $k x + b = 0$ 的解为 $x = 2$ ；②关于x的方程 $k x + b = 3$ 的解为 $x = 0$ ；③当 $x > 2$ 时， $y < 0$ ；④当 $x < 0$ 时， $y < 3$ ．其中正确的是（）

A、①②③ B、①③④ C、②③④ D、①②④

查看试题解析
12. 如图，在同一直角坐标系中，正比例函数 $y = k_{1} x$ ， $y = k_{2} x$ ， $y = k_{3} x$ ， $y = k_{4} x$ 的图象分别为 $l_{1}$ ， $l_{2}$ ， $l_{3}$ ， $l_{4}$ ，则下列关系中正确的是（）

A、 $k_{1} < k_{2} < k_{3} < k_{4}$ B、 $k_{2} < k_{1} < k_{4} < k_{3}$ C、 $k_{1} < k_{2} < k_{4} < k_{3}$ D、 $k_{2} < k_{1} < k_{3} < k_{4}$

查看试题解析

二、填空题

13. 在平面直角坐标系中，如果直线 y＝kx 与函数 y＝ ${\begin{array}{l} 2 x + 4 (x < - 3) \\ - 2 (- 3 \leq x \leq 3) \\ 2 x - 8 (x > 3) \end{array}$ 的图象恰有 3 个不同的交点，则 k的取值范围是.

查看试题解析
14. 函数y= $\frac{x + 1}{\sqrt{x - 1}}$ 中，自变量x的取值范围是．

查看试题解析
15. 一次函数y=kx+b（k≠0）的图象经过A（1，0）和B（0，2）两点，则它的图象不经过第象限．

查看试题解析
16. 若直线y=(k-2)x+2k-1与y轴交于点（0，1），则k的值等于．

查看试题解析
17. 如图，射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象，图中s、t分别表示行驶距离和时间，则这两人骑自行车的速度相差 km/h．

查看试题解析
18. 如图，已知函数y=ax+b和y=cx+d的图象交于点M，则根据图象可知，关于x，y的二元一次方程组 ${\begin{matrix} y = a x + b \\ y = c x + d \end{matrix}$ 的解为．

查看试题解析

三、解答题

19. 甲、乙两人走同一路线都从A地匀速驶向B地，如图是两人行驶路程随时间变化的图象．

(1)、此变化过程中，是自变量，是因变量；

(2)、乙行驶了小时刚好追上甲；

(3)、分别求出甲、乙两人S与t的关系式.

查看试题解析
20. 暑假期间，两名家长计划带领若干名学生去旅游，他们联系了报价均为每人1000元的两家旅行社，经协商，甲旅行社的优惠条件是：两名家长全额收费，学生都按七折收费；乙旅行社的优惠条件是家长、学生都按八折收费．假设这两位家长带领x名学生去旅游，他们应该选择哪家旅行社？

查看试题解析
21. 小明从家骑自行车出发，沿一条直路到相距2400m的邮局办事，小明出发的同时，他的爸爸以96m/min速度从邮局同一条道路步行回家，小明在邮局停留2min后沿原路以原速返回，设他们出发后经过t min时，小明与家之间的距离为s₁ m，小明爸爸与家之间的距离为s₂m，图中折线OABD、线段EF分别表示s₁、s₂与t之间的函数关系的图象．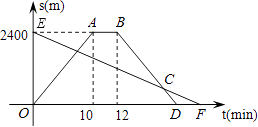

(1)、求s₂与t之间的函数关系式；

(2)、小明从家出发，经过多长时间在返回途中追上爸爸？这时他们距离家还有多远？

查看试题解析
22. 如图，直线 $l_{1}$ 的解析式为 $y_{1} = - 2 x + 2$ ，且 $l_{1}$ 与 $x$ 轴交于点 $D$ ，直线 $l_{2}$ 经过点 $A (4 ， 0)$ ， $(0 ， - 1)$ ，两直线交于点 $C$ .

(1)、求直线 $l_{2}$ 的函数解析式；

(2)、求 $△ A D C$ 的面积.

查看试题解析
23. 山地自行车越来越受到中学生的喜爱，各种品牌相继投放市场，某车行经营的A型车去年销售总额为5万元，今年每辆销售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．
（1）今年A型车每辆售价多少元？（用列方程的方法解答）
（2）该车行计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？
A，B两种型号车的进货和销售价格如下表：

A型车
B型车
进货价格（元）
1100
1400
销售价格（元）
今年的销售价格
2000

查看试题解析
24. 某企业开展献爱心扶贫活动，将购买的60吨大米运往贫困地区帮扶贫困居民，现有甲、乙两种货车可以租用．已知一辆甲种货车和3辆乙种货车一次可运送29吨大米，2辆甲种货车和3辆乙种货车一次可运送37吨大米．

(1)、求每辆甲种货车和每辆乙种货车一次分别能装运多少吨大米？

(2)、已知甲种货车每辆租金为500元，乙种货车每辆租金为450元，该企业共租用8辆货车．请求出租用货车的总费用w（元）与租用甲种货车的数量x（辆）之间的函数关系式．

(3)、在（2）的条件下，请你为该企业设计如何租车费用最少？并求出最少费用是多少元？

查看试题解析

	A型车	B型车
进货价格（元）	1100	1400
销售价格（元）	今年的销售价格	2000