吉林省长春市绿园区2021年中考数学一模试卷
试卷更新日期:2021-05-21 类型:中考模拟
一、单选题
-
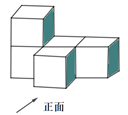
1. 3的绝对值是 ( )A、-3 B、3 C、 D、2. 据国家邮政局统计,2021年农历除夕和初一两天,全国快递处理超130 000 000件,与去年同期相比增长223%,快递的春节“不打烊”服务确保了广大用户能够顺利收到年货,欢度佳节.将130 000 000用科学记数法表示应为( )A、1.3×107 B、13×107 C、1.3×108 D、0.13×1093. 如图所示的是一个由5块大小相同的小正方体搭建成的几何体,则它的左视图是( )
 A、
A、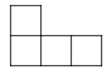 B、
B、 C、
C、 D、
D、 4. 不等式 的解集在数轴上表示正确的是( )A、
4. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,已知 , 平分 , ,则 为( )
5. 如图,已知 , 平分 , ,则 为( )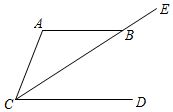 A、 B、 C、 D、6. 如图,菊花1角硬币为外圆内正九边形的边缘异形币,则该正九边形的一个内角的大小为( )
A、 B、 C、 D、6. 如图,菊花1角硬币为外圆内正九边形的边缘异形币,则该正九边形的一个内角的大小为( ) A、 B、 C、 D、7. 如图,在△ABC中,CD,BE分别是△ABC的边AB,AC上的中线,则 ( )
A、 B、 C、 D、7. 如图,在△ABC中,CD,BE分别是△ABC的边AB,AC上的中线,则 ( )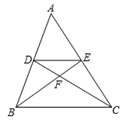 A、 B、 C、 D、8. 如图,以O为圆心的圆与反比例函数 的图象交于 两点,已知点B的坐标为 ,则 的长度为( )
A、 B、 C、 D、8. 如图,以O为圆心的圆与反比例函数 的图象交于 两点,已知点B的坐标为 ,则 的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 实数的大小比较:2 .(填“>”、“=”或“<”)10. 计算:11. 若关于x的一元二次方程 无实数根,则k的取值范围是.12. 如图,在 中, , , ,分别以点 、 为圆心,大于 的长为半径画弧,两弧相交于点 、 ,作直线 交 于点 ,连接 ,则 的长为 .
 13. 如图,在平面直角坐标系中,点P是正比例函数y=x图象上的一点,点A的坐标为(0,1),点B的坐标为(4,1),当PB+PA取最小值时,点P的坐标为 .
13. 如图,在平面直角坐标系中,点P是正比例函数y=x图象上的一点,点A的坐标为(0,1),点B的坐标为(4,1),当PB+PA取最小值时,点P的坐标为 . 14. 如图,某抛物线型桥拱的最大高度为16米,跨度为40米,如图所示建立平面直角坐标系,则该抛物线对应的函数关系式为: .
14. 如图,某抛物线型桥拱的最大高度为16米,跨度为40米,如图所示建立平面直角坐标系,则该抛物线对应的函数关系式为: .
三、解答题
-
15. 先化简,再求值: ,其中 .16. 随着互联网经济的发展,人们的购物模式发生了改变,不带现金也能完成支付,比如使用微信、支付宝、银行卡等.在一次购物中小明和小亮都想从微信(记为A)、支付宝(记为B)、银行卡(记为C)三种支付方式中选择一种方式进行支付.请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.17. 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.(1)、在图1中, 画一个三角形,使它的三边长分别为3,2 , ;(2)、在图2中,画一个钝角三角形,使它的面积为4.
 18. 长春是以汽车产业为主要经济支柱的工业化城市,新中国的第一辆汽车就是在长春诞生的,长春是中国大型的汽车制造城市,所以又叫“汽车城”.某汽车制造厂生产一款电动汽车,计划一个月生产200辆.由于抽调不出足够的熟练工来完成电动汽车的安装,工厂决定招聘一些新工人,他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.(1)、每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)、若工厂现在有熟练工人30人,求还需要招聘多少新工人才能完成一个月的生产计划?19. 如图, 是 的弦, 交 于点 ,过点 的切线交 于点 .
18. 长春是以汽车产业为主要经济支柱的工业化城市,新中国的第一辆汽车就是在长春诞生的,长春是中国大型的汽车制造城市,所以又叫“汽车城”.某汽车制造厂生产一款电动汽车,计划一个月生产200辆.由于抽调不出足够的熟练工来完成电动汽车的安装,工厂决定招聘一些新工人,他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.(1)、每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)、若工厂现在有熟练工人30人,求还需要招聘多少新工人才能完成一个月的生产计划?19. 如图, 是 的弦, 交 于点 ,过点 的切线交 于点 .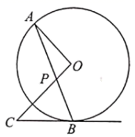 (1)、求证: 是等腰三角形;(2)、若 的半径为 , ,求 的长.20. 为贯彻《关于全面加强新时代大中小学劳动教育的意见》,各学校都在深入开展劳动教育.某校为了解七、八年级学生一学期参加课外劳动时间(用t表示,单位:小时)的情况,从该校七、八年级中各随机抽查了20名学生进行问卷调查,并将调查结果进行整理、描述和分析( ),下面给出了部分信息.
(1)、求证: 是等腰三角形;(2)、若 的半径为 , ,求 的长.20. 为贯彻《关于全面加强新时代大中小学劳动教育的意见》,各学校都在深入开展劳动教育.某校为了解七、八年级学生一学期参加课外劳动时间(用t表示,单位:小时)的情况,从该校七、八年级中各随机抽查了20名学生进行问卷调查,并将调查结果进行整理、描述和分析( ),下面给出了部分信息.七年级抽取的学生在C组的课外劳动时间为: .
八年级抽取的20名学生的课外劳动时间为: .
下表为七、八年级抽取的学生的课外劳动时间的统计量
年级
平均数
众数
中位数
方差
七年级
50
35
a
580
八年级
50
b
50
560

根据以上信息,解答下列问题:
(1)、直接写出 的值. , , , ;(2)、根据以上数据,在该校七、八年级中,你认为哪个年级参加课外劳动的情况较好?请说明理由(一条理由即可);(3)、若该校七、八年级分别有学生400人,试估计该校七、八年级学生一学期课外劳动时间不少于60小时的人数之和.21. 某童装店购进某种品牌的童装若干件,销售了一部分后,剩下的童装每件降价10元销售,全部售完.销售总额y(元)与销售量x(件)之间的函数关系如图所示,请完成下列问题: (1)、降价前该童装的销售单价是元/件;(2)、求a的值;(3)、求降价后销售总额y(元)与销售量x(件)之间的函数关系式,并写出自变量的取值范围.22. 下面是华师版八年级下册数学教材第121页的部分内容.
(1)、降价前该童装的销售单价是元/件;(2)、求a的值;(3)、求降价后销售总额y(元)与销售量x(件)之间的函数关系式,并写出自变量的取值范围.22. 下面是华师版八年级下册数学教材第121页的部分内容.如图,在正方形 中, ,求证: .
 (1)、请根据上述内容,结合图①,写出完整的证明过程.
(1)、请根据上述内容,结合图①,写出完整的证明过程. (2)、如图②,在四边形 中, 交 于点F,交 于点 ,点G是线段 上的一个动点,连结 .当四边形 的面积是4时,线段 的长度为 .
(2)、如图②,在四边形 中, 交 于点F,交 于点 ,点G是线段 上的一个动点,连结 .当四边形 的面积是4时,线段 的长度为 . 23. 如图,在 中, ,动点P从点A出发,沿 以每秒3个单位长度的速度向终点C匀速运动.同时,动点Q从点C出发,沿 以每秒4个单位长度的速度向终点B匀速运动.当点P不与点 重合时,连结 .以直线 为对称轴作 的轴对称图形 .连结 .设点P的运动时间为t秒.
23. 如图,在 中, ,动点P从点A出发,沿 以每秒3个单位长度的速度向终点C匀速运动.同时,动点Q从点C出发,沿 以每秒4个单位长度的速度向终点B匀速运动.当点P不与点 重合时,连结 .以直线 为对称轴作 的轴对称图形 .连结 .设点P的运动时间为t秒. (1)、用含t的代数式表示线段 的长度为;(2)、当直线 与 垂直时,求t的值;(3)、当 是钝角三角形时,求t的取值范围;(4)、当 的一边与 垂直时,直接写出t的值.24. 已知函数 (m为常数且 ),其图象记为G.(1)、当 时,求y的值;(2)、若 ,当G与x轴恰好有两个公共点时,求m的值;(3)、若 ,图象G在 上最低点的纵坐标为 时,求n的值;(4)、当图象G恰有3个点与直线 的距离是 时,直接写出m的取值范围.
(1)、用含t的代数式表示线段 的长度为;(2)、当直线 与 垂直时,求t的值;(3)、当 是钝角三角形时,求t的取值范围;(4)、当 的一边与 垂直时,直接写出t的值.24. 已知函数 (m为常数且 ),其图象记为G.(1)、当 时,求y的值;(2)、若 ,当G与x轴恰好有两个公共点时,求m的值;(3)、若 ,图象G在 上最低点的纵坐标为 时,求n的值;(4)、当图象G恰有3个点与直线 的距离是 时,直接写出m的取值范围.