吉林省延边州2021年中考数学二模试卷
试卷更新日期:2021-05-21 类型:中考模拟
一、单选题
-
1. ﹣4的绝对值等于( )A、﹣ B、 C、﹣4 D、42. 某种细菌的半径约为0.000 0335厘米,将0.000 0335这个数用科学记数法表示为( )A、33.5× B、3.35× C、3.35× D、0.335×3. 某几何体的左视图如图所示,则该几何体不可能是( )
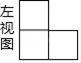 A、
A、 B、
B、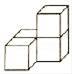 C、
C、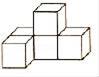 D、
D、 4. 用式子表示“比a的平方的2倍小1的数”为( )A、2a2﹣1 B、(2a)2﹣1 C、2(a﹣1)2 D、(2a﹣1)25. 如图,AE∥DB,∠1=85°,∠2=28°,则∠C的度数为( )
4. 用式子表示“比a的平方的2倍小1的数”为( )A、2a2﹣1 B、(2a)2﹣1 C、2(a﹣1)2 D、(2a﹣1)25. 如图,AE∥DB,∠1=85°,∠2=28°,则∠C的度数为( )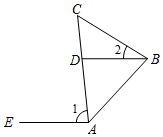 A、55° B、56° C、57° D、60°6. 如图, 、 是 的半径, 是 上一点,连接 、 .若 ,则 的大小为( )
A、55° B、56° C、57° D、60°6. 如图, 、 是 的半径, 是 上一点,连接 、 .若 ,则 的大小为( ) A、126° B、116° C、108° D、106°
A、126° B、116° C、108° D、106°二、填空题
-
7. 分解因式:a2﹣ab= .8. 不等式组 的解集是 .9. 一元二次方程2x2﹣4x+1=0的根的判别式的值为 .10. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡兔各几何?” 设鸡x只,兔y只,可列方程组为.11. 如图,有两堵围墙,有人想测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外,小明提供了测量方案:分别反向延长OA、OB至点C、D,他测量∠COD的度数就是∠AOB的度数,则小明依据的数学道理是 .
 12. 如图, .若 , ,则 的长为.
12. 如图, .若 , ,则 的长为. 13. 如图,OA,OB是⊙O的半径,连接AB并延长到点C,连接OC,若∠AOC=80°,∠C=40°,⊙O的半径为2,则 的长为(结果保留π).
13. 如图,OA,OB是⊙O的半径,连接AB并延长到点C,连接OC,若∠AOC=80°,∠C=40°,⊙O的半径为2,则 的长为(结果保留π). 14. 如图,在平面直角坐标系中,点A(﹣3,0)、点B(0,3),点E在OB上,将△ABE绕点E顺时针旋转90°得到△A'B'E,则A'B'的值为 .
14. 如图,在平面直角坐标系中,点A(﹣3,0)、点B(0,3),点E在OB上,将△ABE绕点E顺时针旋转90°得到△A'B'E,则A'B'的值为 .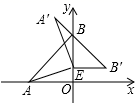
三、解答题
-
15. 先化简,再求值 ,其中 .
16. 小明和小亮进行摸牌游戏,如图,他们有三张除牌面数字不同外、其他完全相同的纸牌,牌面数字分别为4,6,7.他们把纸牌背面朝上,充分洗匀后,从这三张纸牌中随机摸出一张,记下数字放回后,再次重新洗匀,然后再随机摸出一张,再次记下数字.若两次数字之和大于11,则小明胜,否则小亮胜.请你用列表法或画树状图的方法求小明获胜的概率. 17. 用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.18. 如图, ,延长 到 , ,求证: .
17. 用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.18. 如图, ,延长 到 , ,求证: . 19. 图①、图②分别是一把水平放置的椅子的效果图与椅子侧面的示意图,椅子高为AC,椅面宽BE为60cm,椅脚高ED为35cm,且AC⊥BE,AC⊥CD,AC//ED.从点A测得点E的俯角为53°,求椅子高AC.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
19. 图①、图②分别是一把水平放置的椅子的效果图与椅子侧面的示意图,椅子高为AC,椅面宽BE为60cm,椅脚高ED为35cm,且AC⊥BE,AC⊥CD,AC//ED.从点A测得点E的俯角为53°,求椅子高AC.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)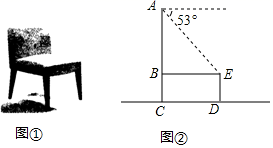 20. 如图,将一个矩形放置在平面直角坐标系中,OA=2,OC=3,E是AB的中点,反比例函数图象过点E且与BC相交于点F.
20. 如图,将一个矩形放置在平面直角坐标系中,OA=2,OC=3,E是AB的中点,反比例函数图象过点E且与BC相交于点F. (1)、求反比例函数的解析式;(2)、连接OE、OF,求四边形OEBF的面积.21. 如图,在6×8的方格纸中有直线l,点A、B、C都在格点上.按要求画四边形,使它的顶点都在格点上,点A、B、C在它的边上(包括顶点).
(1)、求反比例函数的解析式;(2)、连接OE、OF,求四边形OEBF的面积.21. 如图,在6×8的方格纸中有直线l,点A、B、C都在格点上.按要求画四边形,使它的顶点都在格点上,点A、B、C在它的边上(包括顶点). (1)、在图①中画一个轴对称图形,使直线l是对称轴;(2)、在图②中画一个中心对称图形,使直线l平分它的面积.22. 某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如图(单位:分)、整理、分析过程如下,请补充完整.
(1)、在图①中画一个轴对称图形,使直线l是对称轴;(2)、在图②中画一个中心对称图形,使直线l平分它的面积.22. 某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如图(单位:分)、整理、分析过程如下,请补充完整. (1)、按如下分数段整理、描述这两组数据并填写如表:
(1)、按如下分数段整理、描述这两组数据并填写如表:成绩x
学生
70≤x≤74
75≤x≤79
80≤x≤84
85≤x≤89
90≤x≤94
95≤x≤100
甲
乙
1
1
4
2
1
1
(2)、两组数据的平均数、中位数、众数如表所示,填写完整:学生
平均数
中位数
众数
甲
83.7
86
乙
83.7
82
(3)、甲说自己的成绩好,你赞同他的说法吗?请说明理由.23. 甲、乙两个工程队共同开凿一条隧道,甲队按一定的工作效率先施工,一段时间后,乙队从隧道的另一端按一定的工作效率加入施工,中途乙队调离一部分工人去完成其他任务,工作效率降低.当隧道气打通时,甲队工作了40天,设甲,乙两队各自开凿隧道的长度为y(米),甲队的工作时间为x(天),y与x之间的函数图象如图所示. (1)、求甲队的工作效率.(2)、求乙队调离一部分工人后y与x之间的函数关系式(3)、求这条隧道的总长度.24.
(1)、求甲队的工作效率.(2)、求乙队调离一部分工人后y与x之间的函数关系式(3)、求这条隧道的总长度.24. (1)、如图①,在▱ABCD中,点E为CD的中点,连接BE并延长交AD的延长线于点F.求证:点E是BF的中点,点D是AF的中点;(2)、如图②,在四边形ABCD中,AD//BC,∠BAD=90°,AB=4,AD=3,点E是CD的中点,BE⊥CD,BE、AD的延长线相交于点F,则AF= .(3)、如图③,在△ABC中,点D是AC的中点,点E是AB上一点, ,BD,CE相交于点F,则 = .25. 如图,在△ABC中,∠ACB=90°,AC=3,BC=4.动点D从点A出发,以每秒3个单位长度的速度向终点B运动,过点D作AB的垂线交射线AC于点E,过点E在DE右侧作EF⊥DE,且使∠EDF=∠A.设点D运动的时间为t秒.
(1)、如图①,在▱ABCD中,点E为CD的中点,连接BE并延长交AD的延长线于点F.求证:点E是BF的中点,点D是AF的中点;(2)、如图②,在四边形ABCD中,AD//BC,∠BAD=90°,AB=4,AD=3,点E是CD的中点,BE⊥CD,BE、AD的延长线相交于点F,则AF= .(3)、如图③,在△ABC中,点D是AC的中点,点E是AB上一点, ,BD,CE相交于点F,则 = .25. 如图,在△ABC中,∠ACB=90°,AC=3,BC=4.动点D从点A出发,以每秒3个单位长度的速度向终点B运动,过点D作AB的垂线交射线AC于点E,过点E在DE右侧作EF⊥DE,且使∠EDF=∠A.设点D运动的时间为t秒. (1)、用含t的代数式表示EF的长;(2)、当点F落在BC上时,求t的值;(3)、在点D运动的过程中,求△DEF与△ABC重叠部分图形的周长(长度单位)与运动时间t(秒)之间的函数关系式(y>0);(4)、在点D运动的过程中,当△DEF的边被BC平分时,直接t写出的值.26. 如图,在平面直角坐标系中,抛物线 与x轴正半轴交于点A,过点A的直线y=kx+b(k≠0)与该抛物线的另一个交点B的横坐标为2,P是该抛物线上的任意一点,其横坐标为m+1,过点P作x轴的垂线,交直线AB于点C,在该垂线的点P上方取一点D,使PD=1,以CD为边作矩形CDEF,设点E的横坐标为2m.
(1)、用含t的代数式表示EF的长;(2)、当点F落在BC上时,求t的值;(3)、在点D运动的过程中,求△DEF与△ABC重叠部分图形的周长(长度单位)与运动时间t(秒)之间的函数关系式(y>0);(4)、在点D运动的过程中,当△DEF的边被BC平分时,直接t写出的值.26. 如图,在平面直角坐标系中,抛物线 与x轴正半轴交于点A,过点A的直线y=kx+b(k≠0)与该抛物线的另一个交点B的横坐标为2,P是该抛物线上的任意一点,其横坐标为m+1,过点P作x轴的垂线,交直线AB于点C,在该垂线的点P上方取一点D,使PD=1,以CD为边作矩形CDEF,设点E的横坐标为2m. (1)、求直线AB对应的函数关系式;(2)、当点P与点A重合时,求点E的坐标;(3)、当点E在该抛物线上时,求抛物线的顶点到EF的距离;(4)、当矩形CDEF的边CD与该抛物线相交,且该抛物线在矩形CDEF内的部分所对应函数值y随x的增大而增大时,直接写出m的取值范围.
(1)、求直线AB对应的函数关系式;(2)、当点P与点A重合时,求点E的坐标;(3)、当点E在该抛物线上时,求抛物线的顶点到EF的距离;(4)、当矩形CDEF的边CD与该抛物线相交,且该抛物线在矩形CDEF内的部分所对应函数值y随x的增大而增大时,直接写出m的取值范围.