黑龙江省大庆市2021年中考数学一模试卷
试卷更新日期:2021-05-21 类型:中考模拟
一、单选题
-
1. 在实数 , ,0, 中,最小的实数是( ).A、 B、 C、0 D、2. 某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )A、 B、 C、 D、3. 若 与 互为相反数,则 的值为( )A、1 B、-1 C、5 D、-54. 函数y= 中,自变量x的取值范围是( )A、x>﹣2 B、x≥﹣2 C、x>﹣2且x≠1 D、x≥﹣2且x≠15. 已知k1>0>k2 , 则函数y=k1x和y= 的图象在同一平面直角坐标系中大致是( )A、
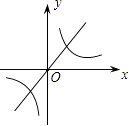 B、
B、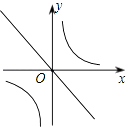 C、
C、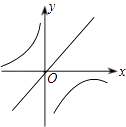 D、
D、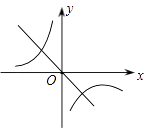 6. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“中”字所在面相对的面上的汉字是( )
6. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“中”字所在面相对的面上的汉字是( )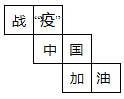 A、油 B、战 C、加 D、役7. 某公司有10名员工,每人年收入数据如下表:
A、油 B、战 C、加 D、役7. 某公司有10名员工,每人年收入数据如下表:年收入/万元
4
6
8
10
人数/人
3
4
2
1
则他们年收入数据的众数与中位数分别为( )
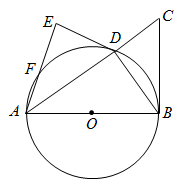
A、4,6 B、6,6 C、4,5 D、6,58. 一个圆锥和一个圆柱的高相等,若要使体积一样,圆锥底面积应是圆柱底面积的( )A、3倍 B、 C、 倍 D、9. 一个三角形支架三条边长分别是75cm,100cm,120cm,现要再做一个与其相似的三角形木架,而只有长为60cm,120cm的两根木条,要求以其中一根为一边,从另一根上截下两段作为另两边(允许有余料),则不同的截法有( )A、一种 B、两种 C、三种 D、四种10. 如图,直线 与 , 轴分别交于点 , ,与直线 交于点 .,在线段 上,动点 以每秒1个单位长度的速度从点 出发向点 做匀速运动,过点 作 轴交直线 于点 ,过点 作 轴交直线 于点 , 轴于点 ,设运动时间为 秒,四边形 的面积为 (点 , 重合除外),在运动过程中,当 时, 的值为( )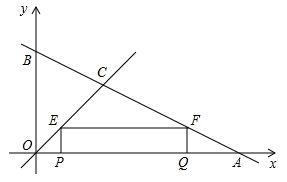 A、 或 B、 或 C、 或 D、 或
A、 或 B、 或 C、 或 D、 或二、填空题
-
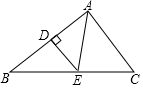
11. 在平面直角坐标系中,点 关于x轴对称的点的坐标为 .12. 因式分解:a2+ab﹣a= .13. 如图,在 中, , 的垂直平分线交 于点 ,交 于点 ,连接 .若 , ,则 的周长为.
 14. 如图,将直尺与30°角的三角尺叠放在一起,若 ,则 .
14. 如图,将直尺与30°角的三角尺叠放在一起,若 ,则 .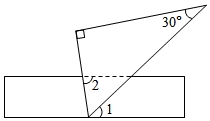 15. 某校九(1)班准备举行一次演讲比赛,甲、乙、丙三人通过抽签方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率是.16. 把黑色三角形按如图所示的规律拼图案,其中第1个图案中有1个黑色三角形,第2个图案中有3个黑色三角形,第3个图案中有6个黑色三角形……按此规律排列下去,则第5个图案中黑色三角形的个数为个.
15. 某校九(1)班准备举行一次演讲比赛,甲、乙、丙三人通过抽签方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率是.16. 把黑色三角形按如图所示的规律拼图案,其中第1个图案中有1个黑色三角形,第2个图案中有3个黑色三角形,第3个图案中有6个黑色三角形……按此规律排列下去,则第5个图案中黑色三角形的个数为个.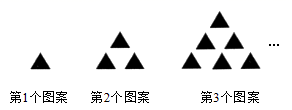 17. 已知一元二次方程 :
17. 已知一元二次方程 :①若方程两根为-1和2,则 ;②若 ,则一元二次方程 有两个不相等的实数根;③若 ,则一元二次方程 有两个不相等的实数根;④若 是方程 的一个根,则一定有 成立.其中正确的是.
18. 如图,边长为2的等边三角形 , 为 内(包括 的边)一动点,且满足 ,则点 运动的路径的长度为.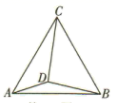
三、解答题
-
19. 计算: .20. 先化简,再求值: ,其中21. 解分式方程:22. 大庆市某校数学兴趣小组借助无人机测量一条河流的宽度 ;如图所示,一架水平飞行的无人机在 处测得正前方河流左岸 处的俯角为 ,无人机沿水平线 方向继续飞行50米至 处,测得正前方河流右岸 处的俯角为30°;线段 的长为无人机距地面的铅直高度,点 , , 在同一条直线上;其中 , 米;求河流的宽度 .(结果精确到1米,参考数据: , )
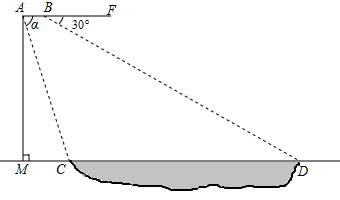 23. 在镇村两委及帮扶人大力扶持下,贫困户周大叔与某公司签定了农产品销售合同,并于今年在自家荒地种植了A,B,C,D四种不同品种的树苗共300棵,其中C品种果树苗的成活率为 ,几个品种果树树苗种植情况及其成活情况分别绘制在下列图①和图②两个尚不完整的统计图中.
23. 在镇村两委及帮扶人大力扶持下,贫困户周大叔与某公司签定了农产品销售合同,并于今年在自家荒地种植了A,B,C,D四种不同品种的树苗共300棵,其中C品种果树苗的成活率为 ,几个品种果树树苗种植情况及其成活情况分别绘制在下列图①和图②两个尚不完整的统计图中.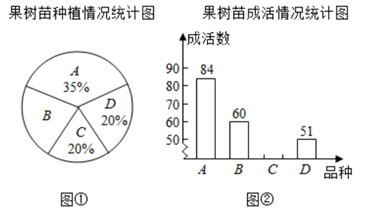 (1)、种植B品种树苗有多少棵;(2)、请你将图②的统计图补充完整;(3)、通过计算说明,哪个品种的果树苗成活率最高?24. 如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交AD,AC,BC于点E,O,F,连接CE和AF.
(1)、种植B品种树苗有多少棵;(2)、请你将图②的统计图补充完整;(3)、通过计算说明,哪个品种的果树苗成活率最高?24. 如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交AD,AC,BC于点E,O,F,连接CE和AF. (1)、求证:四边形AECF为菱形;(2)、若AB=4,BC=8,求菱形AECF的周长.25. 黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.(1)、甲、乙两种商品的进货单价分别是多少?(2)、设甲商品的销售单价为x(单位:元/件),在销售过程中发现:当11≤x≤19时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:
(1)、求证:四边形AECF为菱形;(2)、若AB=4,BC=8,求菱形AECF的周长.25. 黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.(1)、甲、乙两种商品的进货单价分别是多少?(2)、设甲商品的销售单价为x(单位:元/件),在销售过程中发现:当11≤x≤19时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:销售单价x(元/件)
11
19
日销售量y(件)
18
2
请写出当11≤x≤19时,y与x之间的函数关系式.
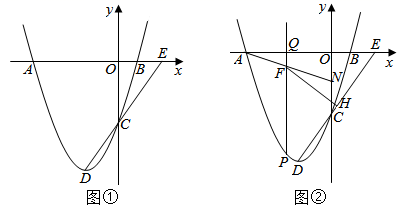
(3)、在(2)的条件下,设甲商品的日销售利润为w元,当甲商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润是多少?26. 如图在平面直角坐标系中,一次函数 的图像经过点 、 交反比例函数 的图像于点 ,点 在反比例函数的图象上,横坐标为 , 轴交直线 于点 , 是 轴上任意一点,连接 、 . (1)、求一次函数和反比例函数的表达式;(2)、求 面积的最大值.
(1)、求一次函数和反比例函数的表达式;(2)、求 面积的最大值.