广东省阳江市阳西县2021年中考数学一模试卷

试卷更新日期：2021-05-21 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算：﹣2﹣5的结果是（）

A、﹣7 B、﹣3 C、3 D、7

查看试题解析
2. 单项式2a的系数是（　　）

A、2 B、2a C、1 D、a

查看试题解析
3. 如图，△ABC中，∠A=60°，∠B=40°，则∠C等于（）

A、100° B、80° C、60° D、40°

查看试题解析
4. 如果把分式 $\frac{2 y}{x + y}$ 中的 $x$ 和 $y$ 都扩大为原来的2倍，那么分式的值（）

A、不变 B、缩小为原来的 $\frac{1}{2}$ C、扩大为原来的2倍 D、扩大为原来的4倍

查看试题解析
5.
在平面直角坐标系中，一次函数y=kx+b的图象如图所示，观察图象可得（）

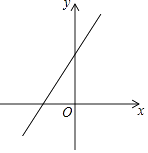A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
6. 若3x＞﹣3y ，则下列不等式中一定成立的是（）

A、 $x + y > 0$ B、 $x - y > 0$ C、 $x + y < 0$ D、 $x - y < 0$

查看试题解析
7. 从 $\sqrt{2}$ ，0，π，3.14，6这5个数中随机抽取一个数，抽到有理数的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
8. 若反比例函数 $y = \frac{k - 1}{x}$ 的图象位于第二、四象限，则k的取值可能是（）

A、0 B、2 C、3 D、4

查看试题解析
9. 如图，将函数y＝ $\frac{1}{2}$ （x﹣2）²+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（）

A、y＝ $\frac{1}{2}$ （x﹣2）²-2 B、y＝ $\frac{1}{2}$ （x﹣2）²+7 C、y＝ $\frac{1}{2}$ （x﹣2）²-5 D、y＝ $\frac{1}{2}$ （x﹣2）²+4

查看试题解析
10. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $∠ A B C = 30 °$ ， $A C = 2$ ， $△ A B C$ 绕点 $C$ 顺时针旋转得到 $△ A_{1} B_{1} C$ ，当点 $A_{1}$ 落在 $A B$ 边上时，连接 $B B_{1}$ ，取 $B B_{1}$ 的中点 $D$ ，连接 $A_{1} D$ ，则 $A_{1} D$ 的长是（）

A、 $\sqrt{7}$ B、 $2 \sqrt{2}$ C、3 D、 $2 \sqrt{3}$

查看试题解析

二、填空题

11. 若- $\sqrt{{(x - 2)}^{2}} = 2 - x$ ，则 $x$ 的取值范围是.

查看试题解析
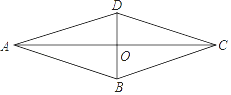
12. 若单项式 $a^{m - 1} b^{2}$ 与 $\frac{1}{2} a^{2} b^{n}$ 的和仍是单项式，则 $n^{m}$ 的值是．

查看试题解析
13. 如图，已知菱形ABCD，对角线AC，BD相交于点O．若tan∠BAC= $\frac{1}{3}$ ，AC=6，则BD的长是．

查看试题解析
14. 已知 $x$ ， $y$ 满足方程组 ${\begin{array}{l} x + 4 y = 12, \\ 2 x - y = 3, \end{array}$ ，则 $x + y$ 的值为．

查看试题解析
15. 将正比例函数 $y = 2 x$ 的图象向上平移3个单位长度，所得的直线不经过第象限．

查看试题解析
16. 如图，AB是⊙O的直径，弦CD⊥AB于点E，⊙O半径为 $\sqrt{3}$ cm，弦CD的长为3 cm，则阴影部分的面积是 cm² ．

查看试题解析
17. 如图，在矩形 $A B C D$ 中， $A B = 5$ ， $B C = 3$ ．将矩形 $A B C D$ 绕点 $B$ 按顺时针方向旋转得到矩形 $G B E F$ ，点 $A$ 落在矩形 $A B C D$ 的边 $C D$ 上的点 $G$ 处，连接 $C E$ ，则 $C E$ 的长是．

查看试题解析

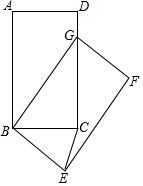
三、解答题

18. 先化简，再求值： $(2 + x) (2 - x) + (x - 1) (x + 5)$ ，其中 $x = \frac{3}{2}$ ．

查看试题解析
19. 在一个不透明的袋子中装有仅颜色不同的 $10$ 个小球，其中红球 $4$ 个，黑球 $6$ 个．

(1)、先从袋子中取出 $m (m > 1)$ 个红球，再从袋子中随机摸出一个球，将“摸出黑球”记为事件 $A$ ．当 $m$ 为何值时，事件 $A$ 是必然事件？

(2)、先从袋子中取出 $m$ 个红球，再放入 $m$ 个一样的黑球并摇匀，若随机摸出 $1$ 个球是黑球的概率等于 $\frac{4}{5}$ ，求 $m$ 的值．

查看试题解析
20. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ．

(1)、请用尺规作图：作 $∠ A$ 的平分线 $A D$ ， $A D$ 交 $B C$ 于点 $D$ ；（保留作图痕迹，不要求写作法）

(2)、若点 $D$ 恰好在线段 $A B$ 的垂直平分线上，求 $∠ B A C$ 的度数．

查看试题解析
21. 如图，在▱ABCD中，DE＝CE，连接AE并延长交BC的延长线于点F.

(1)、求证：△ADE≌△FCE；

(2)、若AB＝2BC，∠F＝36°，求∠B的度数．

查看试题解析
22. 某花店用4500元购进一批花卉和其他植物共2000株进行栽培，已知花卉幼苗每株2元，其他植物幼苗每株3元．

(1)、购进花卉和其他植物幼苗各多少株？

(2)、花店将栽培后的花卉和其他植物全部搭配成500个桌面装饰盆栽．若每个盆栽以15元销售，则可以全部卖完；若每个盆栽涨价1元，则花店每天少销售10个．在不考虑其他费用的情况下，每个盆栽的售价为多少时利润最高？最高利润是多少？

查看试题解析
23. 如图，在平面直角坐标系中， $C$ ， $D$ 是反比例函数 $y = \frac{k}{x}$ 的图象上的两点，以 $C D$ 为边作正方形 $A B C D$ ，点 $A$ ， $B$ 分别在 $x$ 轴、 $y$ 轴的正半轴上，点 $B$ 的坐标为 $(0 ， 1)$ ，且 $∠ A B O = 45 °$ ．

(1)、求 $k$ 的值；

(2)、求 $C D$ 所在直线的解析式．

查看试题解析
24. 如图，点A，B，C，D是直径为AB的⊙O上的四个点，C是劣弧 $\overset{⌢}{B D}$ 的中点，AC与BD交于点E．

(1)、求证：DC²=CE•AC；

(2)、若AE=2，EC=1，求证：△AOD是正三角形；

(3)、在（2）的条件下，过点C作⊙O的切线，交AB的延长线于点H，求△ACH的面积．

查看试题解析
25. 已知抛物线经过 $A (1 ， 0)$ ， $B (3 ， 0)$ ， $C (0 ， 3)$ 三个点．

(1)、求抛物线的解析式；

(2)、如图1，作 $△ O B C$ 的外接圆 $⊙ O^{'}$ ， $D$ 为 $B C$ 上方半圆上一点，当 $\tan ∠ C O D = \frac{1}{2}$ 时，求 $O D$ 的长；

(3)、如图2，直线 $y = x - 2$ 与抛物线交于 $E$ ， $F$ 两点，与 $y$ 轴交于点 $G$ ，作 $y$ 轴的平行线，分别与线段 $E F$ 、抛物线交于 $P$ ， $Q$ 两点（点 $P$ 与点 $E$ ， $F$ 不重合），点 $K$ 为射线 $P E$ 上一点，当 $△ P Q K$ 与 $△ B A C$ 相似时，求 $△ P Q K$ 的最大面积．

查看试题解析