北京市平谷区2021年中考数学一模试卷

试卷更新日期：2021-05-21 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列几何体中，主视图为三角形的是（）

A、 B、 C、 D、

查看试题解析
2. 技术融合打破时空限制，2020服贸会全面上“云”,据悉本届服贸会共有境内外5372家企业搭建了线上电子展台，共举办32场纯线上会议和173场线上直播会议，线上发布项目1870个，发起在线洽谈550000次，将550000用科学记数法表示为（）

A、 $55 \times 10^{4}$ B、 $5.5 \times 10^{5}$ C、 $5.5 \times 10^{6}$ D、 $0.55 \times 10^{6}$

查看试题解析
3. 如图，Rt△ABC中， $∠ A C B = 90 ° ， C D ⊥ A B$ 于点D则下列结论不一定成立的是（）

A、 $∠ 1 + ∠ 2 = 90 °$ B、 $∠ 2 = ∠ 3$ C、 $∠ 1 = ∠ 4$ D、 $∠ 1 = 30 °$

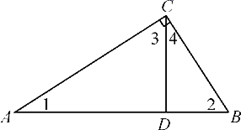查看试题解析
4. 2021年3月20日三星堆遗址的最新考古发现又一次让世界为之瞩目，下列三星堆文物图案中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 正多边形每个内角都是120°，则它的边数为（）

A、5 B、6 C、7 D、8

查看试题解析
6. 实数 $a ， b ， c$ 在数轴上的对应点的位置如图所示.若实数 $a ， b$ 满足 $a + b = 0$ ，则下列结论正确的是（）

A、 $c = 0$ B、 $b < 0$ C、 $c > 0$ D、 $c < 0$

查看试题解析
7. 不透明袋子中有 $1$ 个红球和 $2$ 个绿球，这些球除颜色外无其他差别．从袋子中随机取出 $1$ 个球，恰好是红球的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $1$

查看试题解析
8. 学习完函数的有关知识之后，强强对函数产生了浓厚的兴趣，他利用绘图软件画出函数 $y = \frac{1}{x + 2}$ 的图象并对该函数的性质进行了探究．下面推断正确的是（   ）

①该函数的定义域为 $x \neq - 2$ ；

②该函数与x轴没有交点；

③该函数与y轴交于点 $(0 ， \frac{1}{2})$ ；

④若 $(x_{1} ， y_{1}) ， (x_{2} ， y_{2})$ 是该函数上两点，当 $x_{1} < x_{2}$ 时，一定有 $y_{1} > y_{2}$ .

A、①②③④ B、①③ C、① ②③ D、②③④

查看试题解析

二、填空题

9. 若代数式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
10. 分解因式： $a x^{2} - a y^{2} =$ ．

查看试题解析
11. 写出一个比 $\sqrt{2}$ 大且比 $\sqrt{10}$ 小的整数.

查看试题解析
12. 化简： $1 - \frac{1}{a + 1} =$ .

查看试题解析
13. 如图，在 $Δ A B C$ 和 $Δ A D C$ 中， $A B ⊥ B C$ ， $A D ⊥ D C$ ，只需添加一个条件即可证明 $Δ A B C ≌ Δ A D C$ ，这个条件可以是（写出一个即可）.

查看试题解析
14. 《孙子算经》记载：今有3人共车，二车空；二人共车，九人步，问人与车各几何？译文：今有若干人乘车，若每三人共乘一辆车，最终剩余2辆车；若每2人共乘一辆车，最终剩余9人无车可乘．问共有多少人？多少辆车？若设有x辆车，有y人，则可列方程组为．

查看试题解析
15. 如图所示的网格是正方形网格， $A ， B ， C ， D$ 是网格线交点，则 $Δ A B O$ 的面积与 $Δ C D O$ 的面积的大小关系为： $S_{△ A B O}$ $S_{△ C D O}$ （填“>”，“=”或“<”） .

查看试题解析
16. 某种预防病虫害的农药即将于三月上旬喷洒，需要连续三天完成，又知当最低温度不低于0摄氏度，且昼夜温差不大于10摄氏度时药物效果最佳，为此农广站工作人员查看了三月上旬天气预报，请你结合气温图给出一条合理建议，药剂喷洒可以安排在日开始进行.

查看试题解析

三、解答题

17. 计算： ${(\frac{1}{2})}^{-1} + \sqrt{12} + | \sqrt{3} - 2 | - {3tan30}^{o}$

查看试题解析
18. 解不等式组： ${\begin{matrix} 3 x + 1 > 2 x \\ \frac{x + 3}{2} \geq x \end{matrix}$

查看试题解析
19. 先化简，再求值： $x^{2} + 2 x - 1 = 0$ ，求代数式 $(x - 1) (x + 1) + 2 (x - 3)$ 的值．

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} + (k + 1) x + k = 0$ ．

(1)、求证：方程总有两个实数根；

(2)、选择一个你喜欢的k值代入，并求此时方程的解.

查看试题解析
21. 已知：如图， $∠ M A N = α (0^{°} < α < 45^{°})$

求作： $Δ A B C$ ，使得 $∠ A B C = 2 ∠ B A C$ ，

作法：①在射线 $A N$ 上取点 $O$ ，以点 $O$ 为圆心， $O A$ 长为半径画圆，交射线 $A M$ 于点 $C$ ；

②连接 $CO$

③以点 $C$ 为圆心， $CO$ 长为半径画弧，交射线 $A N$ 于点 $B$ ；连接 $C B$

线段 $Δ A B C$ 就是所求作

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明
证明：

∵点 $C$ 、 $A$ 在 $⊙ O$ 上.

∴ $∠ C O B = 2 ∠ C A B$ （）（填推理依据）.

∵ $C B = C O$

∴ $∠ C B A =$ .

∴ $∠ C B A =2 ∠ C A B$

查看试题解析
22. 已知：直线 $l_{1} ： y = k x + b$ 过点 $A$ （ $- 1$ ， $0$ ），且与双曲线 $l_{2}$ ： $y = \frac{2}{x}$ 相交于点 $B$ （ $- 1 < x_{1} < x_{2} < 1$ ，2）．

(1)、求m值及直线 $l_{1}$ 的解析式；

(2)、画出 $l_{1} ， l_{2}$ 的图象，结合图象直接写出不等式 $k x + b > \frac{2}{x}$ 的解集．

查看试题解析
23. 如图， $R t Δ A B C$ 中， $∠ A B C = 90 °$ ，D是AC的中点，连接BD，过点C作CE//BD，过点B作BE//AC两直线相交于点E.

(1)、求证：四边形 $D B E C$ 是菱形；

(2)、若 $∠ A = 30 ° ， B C = 2$ ，求四边形 $D B E C$ 的面积.

查看试题解析
24. 如图，点E是 $⊙ O$ 中弦AB的中点，过点E作 $⊙ o$ 的直径CD，P是 $⊙ O$ 上一点，过点P作 $⊙ o$ 的切线，与AB的延长线交于F，与CD的延长线交于点G，连接CP与AB交于点M

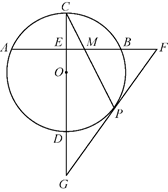(1)、求证：FM=FP；

(2)、若点P是FG的中点， $\cos ∠ F = \frac{3}{5}$ ， $⊙ O$ 半径长为3，求EM长

查看试题解析
25. “十三五”时期是北京市迄今为止大气污染治理力度最大，成效最明显的五年，2020年空气质量优良天数继续增加，大气主要污染物中细颗粒物（PM2.5）年均浓度首次实现38微克/立方米，空气质量改善取得标志性、历史性突破。下面对2013--2020年北京市的空气质量有关数据进行收集、整理、描述和分析，给出了部分信息：

a.2013-2020年北京市空气质量指数为优良级别天数变化

b. 收集了2021年3月北京市16个城区的PM2.5的浓度均值（单位：微克/立方米），79 79 80 81 83 79 83 83 81 83 84 84 84 84 86 84并整理如下表：

PM2.5的浓度

79

80

81

83

84

86

区的个数

m

1

2

n

5

1

C.2021年3月北京市每日的PM2.5的浓度（单位：微克/立方米）统计情况如下：

(1)、2020年北京市空气质量优良天数比2013年增加了天；

(2)、m的值为；n的值为；

(3)、2021年3月北京市16个城区的PM2.5浓度值的中位数是；

(4)、依据2021年3月北京市每日的PM2.5的浓度情况统计图，若三月上旬（1-15日）北京市的PM2.5的浓度平均值为 $\overline{x_{1}}$ ，方差为S₁² ，三月下旬（16-31日）北京市的PM2.5的浓度平均值为 $\overline{x_{2}}$ ，方差为S₂² ，则 $\overline{x_{1}}$ $\overline{x_{2}}$ ，S₁²S₂²（填“>”，“=”或“<”）；

查看试题解析
26. 已知关于 $x$ 的二次函数 $y = x^{2} - 2 m x - 3$ ．

(1)、当抛物线过点（2，-3）时，求抛物线的表达式，并求它与y轴的交点坐标；

(2)、求这个二次函数的对称轴（用含m的式子表示）；

(3)、若抛物线上存在两点 $A (a ， a)$ 和 $B (b ， - b)$ ，当 $a < 0 ， b > 0$ 时，总有 $a + b > 0$ ，求m的取值范围．

查看试题解析
27. 在 $Δ A B C$ 中， $∠ A C B = 90 ° ， A C = B C$ ， $D$ 是直线 $A B$ 上一点（点D不与点A、B重合），连接DC并延长到E，使得CE=CD，过点E作 $E F ⊥ B C$ ，交直线 $B C$ 于点 $F$

(1)、如图1，当点D为线段 $A B$ 的上任意一点时，用等式表示线段EF、CF、AC的数量关系，并证明；

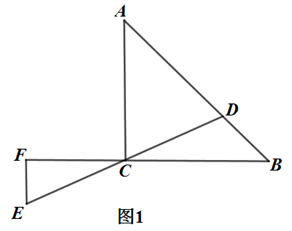(2)、如图2，当点D为线段 $B A$ 的延长线上一点时，依题意补全图2，猜想线段EF、CF、AC的数量关系是否发生改变，并证明；

查看试题解析
28. 已知点P、Q分别为图形M和图形N上的任意点，若存在点P、Q使得PQ=1，我们就称图形M、N为友好图形，P、Q为关于图形M、N的一对友好点．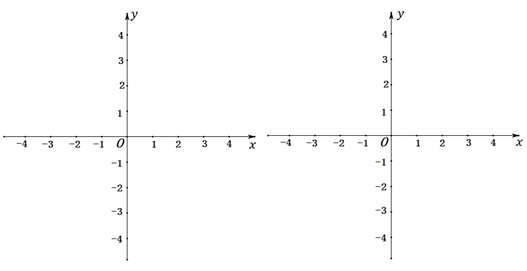

(1)、已知点 $A (1 ， 0)$ ， $B (0 ， \frac{1}{2})$ ，C（-1，1）中，与点O为一对友好点，

(2)、已知 $⊙$ O半径r=1，若直线 $y = x + b$ 与 $⊙$ O有且只有一对友好点，求b的值；

(3)、已知点， $D (m ， \sqrt{2})$ ， $⊙$ D半径r=1，若直线y=x+m 与 $⊙$ D是友好图形，求m的取值范围．

查看试题解析

PM2.5的浓度	79	80	81	83	84	86
区的个数	m	1	2	n	5	1