北京市丰台区2021年中考数学一模试卷
试卷更新日期:2021-05-21 类型:中考模拟
一、单选题
-
1. 一个几何体的三视图如图所示,该几何体是( )
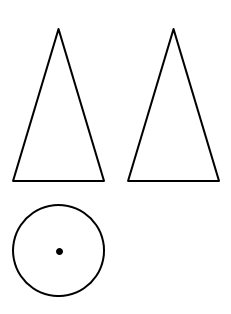 A、
A、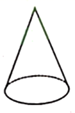 B、
B、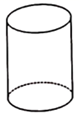 C、
C、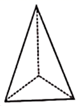 D、
D、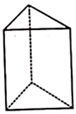 2. 经过全党全国各族人民共同努力,在迎来中国共产党成立一百周年的重要时刻,我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫,将9899用科学记数法表示应为( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形也是中心对称图形的是( )A、
2. 经过全党全国各族人民共同努力,在迎来中国共产党成立一百周年的重要时刻,我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫,将9899用科学记数法表示应为( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形也是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图, , 平分 .下列说法错误的是( )
4. 如图, , 平分 .下列说法错误的是( ) A、 B、 C、 D、5. 将边长分别为2和4的长方形如图剪开,拼成一个正方形,则该正方形的边长最接近整数( )
A、 B、 C、 D、5. 将边长分别为2和4的长方形如图剪开,拼成一个正方形,则该正方形的边长最接近整数( )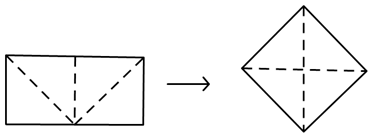 A、1 B、2 C、3 D、46. A,B是数轴上位于原点O异侧的两点(点A在点B的左侧),若点A,B分别对应的实数为a,b,且 ,则 中最大的数是( )A、 B、 C、 D、7. 2022年冬奥会吉祥物为“冰墩墩”,冬残奥会吉祥物为“雪容融”.如图,现有三张正面印有吉祥物的不透明卡片,卡片除正面图案不同外,其余均相同,其中两张正面印有冰墩墩图案,一张正面印有雪容融图案,将三张卡片正面向下洗匀,从中随机抽取两张卡片,则抽出的两张都是冰墩墩卡片的概率是( )
A、1 B、2 C、3 D、46. A,B是数轴上位于原点O异侧的两点(点A在点B的左侧),若点A,B分别对应的实数为a,b,且 ,则 中最大的数是( )A、 B、 C、 D、7. 2022年冬奥会吉祥物为“冰墩墩”,冬残奥会吉祥物为“雪容融”.如图,现有三张正面印有吉祥物的不透明卡片,卡片除正面图案不同外,其余均相同,其中两张正面印有冰墩墩图案,一张正面印有雪容融图案,将三张卡片正面向下洗匀,从中随机抽取两张卡片,则抽出的两张都是冰墩墩卡片的概率是( ) A、 B、 C、 D、8. 如图,在物理课上,老师将挂在弹簧测力计下端的铁块浸没于水中,然后缓慢匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧测力计的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的大致图象是( )
A、 B、 C、 D、8. 如图,在物理课上,老师将挂在弹簧测力计下端的铁块浸没于水中,然后缓慢匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧测力计的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的大致图象是( )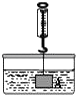 A、
A、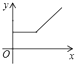 B、
B、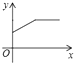 C、
C、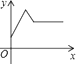 D、
D、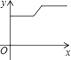
二、填空题
-
9. 要使分式 有意义,则实数 的取值范围是 .10. 方程组 的解为 .11. 正八边形的每个外角为度.
12. 如图, 平分 ,点B在射线 上,若使 ,则还需添加的一个条件是(只填一个即可). 13. 写出一个图象开口向上,顶点在x轴上的二次函数的解析式 .14. 在平面直角坐标系 中,直线 与双曲线 交于 , 两点,则 的值为 .15. 如图所示的网格是正方形网格,则 (点A,B,C,D,E是网格线交点).
13. 写出一个图象开口向上,顶点在x轴上的二次函数的解析式 .14. 在平面直角坐标系 中,直线 与双曲线 交于 , 两点,则 的值为 .15. 如图所示的网格是正方形网格,则 (点A,B,C,D,E是网格线交点). 16. 京剧作为一门中国文化的传承艺术,常常受到外国友人的青睐.如图,在平面直角坐标系 中,某脸谱轮廓可以近似地看成是一个半圆与抛物线的一部分组合成的封闭图形,记作图形G.点A,B,C,D分别是图形G与坐标轴的交点,已知点D的坐标为 , 为半圆的直径,且 ,半圆圆心M的坐标为 .关于图形G给出下列四个结论,其中正确的是(填序号).
16. 京剧作为一门中国文化的传承艺术,常常受到外国友人的青睐.如图,在平面直角坐标系 中,某脸谱轮廓可以近似地看成是一个半圆与抛物线的一部分组合成的封闭图形,记作图形G.点A,B,C,D分别是图形G与坐标轴的交点,已知点D的坐标为 , 为半圆的直径,且 ,半圆圆心M的坐标为 .关于图形G给出下列四个结论,其中正确的是(填序号).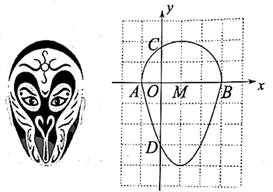
①图形G关于直线 对称;
②线段 的长为 ;
③图形G围成区域内(不含边界)恰有12个整点(即横、纵坐标均为整数的点);
④当 时,直线 与图形G有两个公共点.
三、解答题
-
17. 计算: .18. 解不等式组:19. 已知 ,求代数式 的值.20. 关于x的一元二次方程 .(1)、若方程的一个根为1,求m的值;(2)、求证:方程总有两个不相等的实数根.21. 已知:在 中,AB=AC,AD是边BC上的中线.
求作:∠BPC,使∠BPC=∠BAC.
作法:
①作线段 的垂直平分线 ,与直线 交于点O;
②以点O为圆心, 长为半径作 ;
③在 上取一点P(不与点A重合),连接 , . 就是所求作的角.
 (1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接 .
∵ 是线段 的垂直平分线,
∴ ▲ .
∵ 是边 上的中线,
∴ .
∴ .
∴ 为 的外接圆.
∵点P在 上,
∴ ( ▲ )(填推理的依据).
22. 如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作 于点E,延长BC到点F,使CF=BE,连接DF.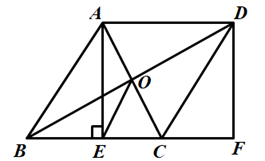 (1)、求证:四边形AEFD是矩形;(2)、连接OE,若AD=10,EC=4,求OE的长度.23. 在平面直角坐标系 中,将点A(m,2)向左平移2个单位长度,得到点B,点B在直线 上.(1)、求m的值和点B的坐标;(2)、若一次函数 的图象与线段 有公共点,求k的取值范围.24. 如图, 为 的直径,点C在 上,过点C作 的切线 ,过点A作 于点D,交 的延长线于点E.
(1)、求证:四边形AEFD是矩形;(2)、连接OE,若AD=10,EC=4,求OE的长度.23. 在平面直角坐标系 中,将点A(m,2)向左平移2个单位长度,得到点B,点B在直线 上.(1)、求m的值和点B的坐标;(2)、若一次函数 的图象与线段 有公共点,求k的取值范围.24. 如图, 为 的直径,点C在 上,过点C作 的切线 ,过点A作 于点D,交 的延长线于点E.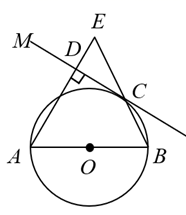 (1)、求证: ;(2)、若 , ,求 的长.25. 劳动是成功的必由之路,是创造价值的源泉. 某校为引导学生崇尚劳动,尊重劳动,在劳动中提升综合素质,对九年级(1)班35名学生进行了劳动能力量化评估(劳动能力量化评估的成绩采用十分制)和近一周家务劳动总时间调查,并对相关数据进行了收集、整理和分析,研究过程中的相关数据如下:
(1)、求证: ;(2)、若 , ,求 的长.25. 劳动是成功的必由之路,是创造价值的源泉. 某校为引导学生崇尚劳动,尊重劳动,在劳动中提升综合素质,对九年级(1)班35名学生进行了劳动能力量化评估(劳动能力量化评估的成绩采用十分制)和近一周家务劳动总时间调查,并对相关数据进行了收集、整理和分析,研究过程中的相关数据如下:劳动能力量化成绩与近一周家务劳动总时间统计图

根据以上信息,回答下列问题:
(1)、九年级(1)班劳动能力量化成绩的中位数所在的分数段为(填序号);① ② ③ ④ ⑤
(2)、下列说法合理的是(填序号);①班主任老师对近一周家务劳动总时间在4小时以上,且劳动能力量化成绩取得9分以上的学生进行表彰奖励,恰有3人获奖;
②小颖推断劳动能力量化成绩分布在 的同学近一周家务劳动总时间主要分布在 的时间段.
(3)、你认为普遍情况下参加家务劳动的时间与劳动能力之间具有怎样的关系?26. 在平面直角坐标系 中,抛物线 .(1)、若抛物线过点 ,求抛物线的对称轴;(2)、若 为抛物线上两个不同的点.①当 时, ,求a的值;
②若对于 ,都有 ,求a的取值范围.
27. 如图,在 中, , ,点P在线段 ,作射线 ,将射线 绕点C逆时针旋转 ,得到射线 ,过点A作 于点D,交 于点E,连接 .(1)、依题意补全图形;(2)、用等式表示线段 , , 之间的数量关系,并证明.28. 如图,直线l和直线l外一点P,过点P作 于点H任取直线l上点Q,点H关于直线 的对称点为点 ,标点 为点P关于直线l的垂对点.在平面直角坐标系 中, (1)、已知点 ,则点 中是点P关于x轴的垂对点的是;(2)、已知点 ,且 ,直线 上存在点M关于x轴的垂对点,求m的取值范围;(3)、已知点 ,若直线 上存在两个点N关于x轴的垂对点,直接写出n的取值范围,
(1)、已知点 ,则点 中是点P关于x轴的垂对点的是;(2)、已知点 ,且 ,直线 上存在点M关于x轴的垂对点,求m的取值范围;(3)、已知点 ,若直线 上存在两个点N关于x轴的垂对点,直接写出n的取值范围,