北京市东城区2021年中考数学一模试卷
试卷更新日期:2021-05-21 类型:中考模拟
一、单选题
-
1. 某几何体的三种视图如图所示,则该几何体是( )
 A、三棱柱 B、长方体 C、圆柱 D、圆锥2. 在平面直角坐标系 中,下列函数的图象不过点 的是( )A、 B、 C、 D、3. 2020年7月23日,中国首颗火星探测器“天问一号”成功发射.2021年2月10日,在经过长达七个月,475 000 000公里的漫长飞行之后,“天问一号”成功进入火星轨道.将475000000科学记数法表示应为( )A、 B、 C、 D、4. 一副三角板如图放置,斜边互相平行,且每个三角板的直角顶点都在另一个三角板的斜边上,在图中所标记的角中,与 相等的角是( )
A、三棱柱 B、长方体 C、圆柱 D、圆锥2. 在平面直角坐标系 中,下列函数的图象不过点 的是( )A、 B、 C、 D、3. 2020年7月23日,中国首颗火星探测器“天问一号”成功发射.2021年2月10日,在经过长达七个月,475 000 000公里的漫长飞行之后,“天问一号”成功进入火星轨道.将475000000科学记数法表示应为( )A、 B、 C、 D、4. 一副三角板如图放置,斜边互相平行,且每个三角板的直角顶点都在另一个三角板的斜边上,在图中所标记的角中,与 相等的角是( ) A、 B、 C、 D、5. 如图, 经过旋转或轴对称得到 ,其中 绕点A逆时针旋转 的是( )A、
A、 B、 C、 D、5. 如图, 经过旋转或轴对称得到 ,其中 绕点A逆时针旋转 的是( )A、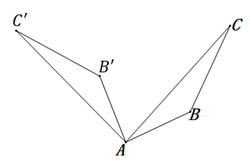 B、
B、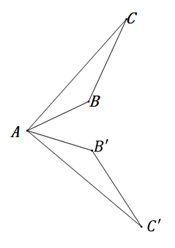 C、
C、 D、
D、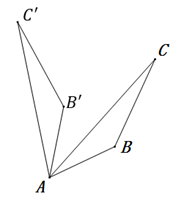 6. 实数a,b,c在数轴上的对应点的位置如图所示,下列式子正确的是( )
6. 实数a,b,c在数轴上的对应点的位置如图所示,下列式子正确的是( ) A、b+c>0 B、a-b>a-c C、ac>bc D、ab>ac7. 如图,PA,PB是 的切线,切点分别为A,B, PO的延长线交 于点C,连接OA,OB,BC.若 ,则 等于( )
A、b+c>0 B、a-b>a-c C、ac>bc D、ab>ac7. 如图,PA,PB是 的切线,切点分别为A,B, PO的延长线交 于点C,连接OA,OB,BC.若 ,则 等于( ) A、 B、 C、 D、8. 一个直角三角形木架的两条直角边的边长分别是 , .现要做一个与其相似的三角形木架,如果以 长的木条为其中一边,那么另两边中长度最大的一边最多可达到( )A、 B、 C、 D、
A、 B、 C、 D、8. 一个直角三角形木架的两条直角边的边长分别是 , .现要做一个与其相似的三角形木架,如果以 长的木条为其中一边,那么另两边中长度最大的一边最多可达到( )A、 B、 C、 D、二、填空题
-
9. 若分式 的值为0,则x的值等于 .10. 分解因式: .11. 用一组 , 的值说明命题“若 ,则 ”是错误的,这组值可以是 ,12. 4月23日是世界读书日,甲、乙两位同学在读书日到来之际共购买图书22本,其中甲同学购买的图书数量比乙同学购买的图书数量的2倍多1,求甲、乙两位同学分别购买的图书数量.设甲同学购买图书x本、乙同学购买图书y本,则可列方程组为 .13. 有人做了掷骰子的大量重复试验,统计结果如下表所示:
投掷次数(n)
“出现点数为1”的次数(频数m)
频率
300
52
0.173
400
65
0.163
500
80
0.160
600
99
0.165
700
114
0.163
800
136
0.170
900
151
0.168
1000
166
0.166
根据上表信息,掷一枚骰子,估计“出现点数为1”的概率为(精确到0.001)
14. 若一个多边形的内角和是外角和的两倍,则该多边形的边数是 .15. 若关于x的一元二次方程 有两个相等的实数根,则c的最小值是 .16. 小青要从家去某博物馆参加活动,经过查询得到多种出行方式,可选择的交通工具有地铁、公交车、出租车、共享单车等,小青的家到地铁站(或公交车站)有一段距离,地铁站(或公交车站)到该博物馆也有一段距离,需要步行或骑共享单车,共享单车的计价规则为:每30分钟1.5元,不足30分钟的按30分钟计算,出行方式的相应信息如下表(√表示某种出行方式选择的交通工具);乘出租车
乘坐
公交车
乘坐地铁
骑共享
单车
共需步行
(公里)
总用时
(分钟)
费用
(元)
方式1
√
2.0
47
4
方式2
√
56
3
方式3
√
1.6
78
3
方式4
√
1.8
80
3
方式5
√
√
1.5
60
6
方式6
√
√
1.6
56
6
方式7
√
√
1.7
55
6
方式8
√
√
1.5
57
6
方式9
√
0.2
32
41
根据表格中提供的信息,小青得出以下四个推断:
①要使费用尽可能少,可以选择方式2,3,4;
②要使用时较短,且费用较少,可以选择方式1;
③如果选择公交车和地铁混合的出行方式,平均用时约57分钟;
④如果将上述出行方式中的“步行”改为“骑共享单车”,那么除方式2外,其它出行方式的费用均会超过8元.
其中推断合理的是(填序号).
三、解答题
-
17. 计算: .18. 已知 ,求代数式 的值.19. 尺规作图:如图,已知线段a,线段b及其中点.

求作:菱形ABCD,使其两条对角线的长分别等于线段a,b的长.
作法:①作直线m,在m上任意截取线段 ;
②作线段AC的垂直平分线EF交线段AC于点O;
③以点O为圆心,线段b的长的一半为半径画圆,交直线EF于点B,D;
④分别连接AB,BC,CD,DA;
则四边形ABCD就是所求作的葵形.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹) (2)、完成下面的证明.
(2)、完成下面的证明.证明: ,
四边形ABCD是 ▲ .
,
四边形ABCD是菱形( ▲ )(填推理的依据).
20. 解不等式组: ,并写出其中的正整数解.21. 解分式方程: .22. 如图,在平行四边形ABCD中,过点D作 于点E,DE的延长线交AB于点F,过点B作 交DC于点G,交AC于点M.过点G作 于点N.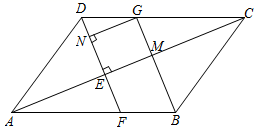 (1)、求证:四边形NEMG为矩形;(2)、若 ,求线段AC的长.23. 在平面直角坐标系 中,直线 与直线 平行,且过点 .(1)、求直线 的表达式;(2)、横、纵坐标都是整数的点叫作整点.直线 与直线 关于y轴对称,直线 与直线 围成的区域W内(不包含边界)恰有6个整点,求m的取值范围.24. 如图, 是 的内接三角形,过点C作 的切线交AB的延长线于点D, 于点E,交CD于点F.
(1)、求证:四边形NEMG为矩形;(2)、若 ,求线段AC的长.23. 在平面直角坐标系 中,直线 与直线 平行,且过点 .(1)、求直线 的表达式;(2)、横、纵坐标都是整数的点叫作整点.直线 与直线 关于y轴对称,直线 与直线 围成的区域W内(不包含边界)恰有6个整点,求m的取值范围.24. 如图, 是 的内接三角形,过点C作 的切线交AB的延长线于点D, 于点E,交CD于点F.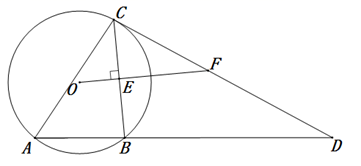 (1)、求证: ;(2)、若 ,求线段CF的长.25. 第24届冬季奥林匹克运动会,又称2022年北京冬奥会,将于2022年2月4日至2月20日,在北京市和张家口市同时举行,为了调查同学们对冬奥知识的了解情况,小冬从初中三个年级各随机抽取10人,进行了相关测试,获得了他们的成绩(单位:分),并对数据(成绩)进行了整理、描述和分析,下而给出了相关信息:
(1)、求证: ;(2)、若 ,求线段CF的长.25. 第24届冬季奥林匹克运动会,又称2022年北京冬奥会,将于2022年2月4日至2月20日,在北京市和张家口市同时举行,为了调查同学们对冬奥知识的了解情况,小冬从初中三个年级各随机抽取10人,进行了相关测试,获得了他们的成绩(单位:分),并对数据(成绩)进行了整理、描述和分析,下而给出了相关信息:a.30名同学冬奥知识测试成绩的统计图如下:

b.30名同学冬奥知识测试成绩的频数分布直方图如下(数据分成6组: , , ,
):
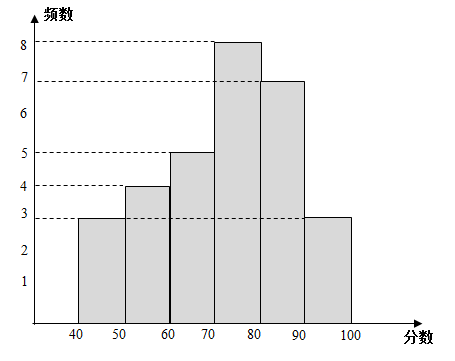
c.测试成绩在 这一组的是:
70 73 74 74 75 75 77 78
d.小明的冬奥知识测试成绩为85分
根据以上信息,回答下列问题:
(1)、小明的测试成绩在抽取的30名同学的成绩中从高到低排名第;(2)、抽取的30名同学的成绩的中位数为;(3)、序号为1-10的学生是七年级的,他们的成绩的方差记为 ;序号为11-20的学生是八年级的,他们的成绩的方差记为 ;序号为21-30的学生是九年级的,他们的成绩的方差记为 .直接写出 的大小关系;(4)、成绩80分及以上记为优秀,若该校初中三个年级420名同学都参加测试,估计成绩优秀的同学约为人.26. 在平面直角坐标系 中,点 在抛物线 上,其中 .(1)、求抛物线的对称轴(用含a的式子表示);(2)、①当 时,求y的值;②若 ,求x1的值(用含a的式子表示);
(3)、若对于 ,都有 ,求a的取值范围.27. 已知 ,点B为边AM上一个定点,点P为线段AB上一个动点(不与点A,B重合),点P关于直线AN的对称点为点Q,连接 .点A关于直线BQ的对称点为点C,连接 .(1)、如下图,若P为线段AB的中点.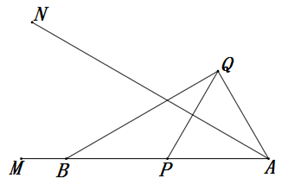
①直接写出 的度数;
②依题意补全图形,并直接写出线段CP与AP的数量关系;
(2)、如下图,若线段CP与BQ交于点D.
①设 ,求 的大小(用含a的式子表示);
②用等式表示线段 之间的数量关系,并证明.
28. 在平面直角坐标系 中,已知正方形 ,其中 ,M,N为该正方形外两点, .给出如下定义:记线段MN的中点为P,平移线段MN得到线段 ,使点 分别落在正方形 的相邻两边上,或线段 与正方形的边重合( 分别为点M,N,P的对应点),线段 长度的最小值称为线段MN到正方形 的“平移距离”.(1)、如下图,平移线段MN,得到正方形 内两条长度为1的线段 ,则这两条线段的位置关系是;若 分别为 的中点,在点 中,连接点P与点的线段的长度等于线段MN到正方形 的“平移距离”; (2)、如图,已知点 ,若M,N都在直线BE上,记线段MN到正方形 的“平移距离”为 ,求 的最小值;
(2)、如图,已知点 ,若M,N都在直线BE上,记线段MN到正方形 的“平移距离”为 ,求 的最小值; (3)、若线段MN的中点P的坐标为 ,记线段MN到正方形 的“平移距离”为 ,直接写出 的取值范围.
(3)、若线段MN的中点P的坐标为 ,记线段MN到正方形 的“平移距离”为 ,直接写出 的取值范围.