安徽省芜湖市2021年中考数学二模试卷
试卷更新日期:2021-05-21 类型:中考模拟
一、单选题
-
1. 在3,﹣3,0,﹣2这四个数中,最小的数是( )A、3 B、﹣3 C、0 D、﹣22. 下列运算正确的是( )A、 B、 C、 D、3. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是( )
 A、
A、 B、
B、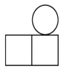 C、
C、 D、
D、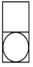 4. 2021年全国两会《政府工作报告》中指出,年初剩余的551万农村贫困人口全部脱贫.数据551万用科学记数法可以表示为( )A、 B、 C、 D、5. 下列方程中,无实数根的方程是( )A、 B、 C、 D、6. 某旅游景区去年第二季度游客数量比第一季度下降20%,第三、四季度游客数量持续增长,第四季度游客数量比第一季度增长15.2%,设第三、四季度的平均增长率为 ,下列方程正确的是( )A、 B、 C、 D、7. 一次函数
4. 2021年全国两会《政府工作报告》中指出,年初剩余的551万农村贫困人口全部脱贫.数据551万用科学记数法可以表示为( )A、 B、 C、 D、5. 下列方程中,无实数根的方程是( )A、 B、 C、 D、6. 某旅游景区去年第二季度游客数量比第一季度下降20%,第三、四季度游客数量持续增长,第四季度游客数量比第一季度增长15.2%,设第三、四季度的平均增长率为 ,下列方程正确的是( )A、 B、 C、 D、7. 一次函数 满足
满足 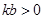 ,且
,且  随 x 的增大而减小,则此函数的图象不经过( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 在 中, , , ,则 的长为( )A、1 B、2 C、 或4 D、2或49. 如图,矩形 中, , .若 是矩形 边上一动点,且使得 ,则这样的点 有( )
随 x 的增大而减小,则此函数的图象不经过( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 在 中, , , ,则 的长为( )A、1 B、2 C、 或4 D、2或49. 如图,矩形 中, , .若 是矩形 边上一动点,且使得 ,则这样的点 有( ) A、1个 B、2个 C、3个 D、4个10. 如图所示,点P是边长为1的正方形 对角线 上一动点(P与点A、C不重合),点E在 上,且 ,设 , 的面积为y,则下列图象中,能表示y与x函数关系的图象大致是( )
A、1个 B、2个 C、3个 D、4个10. 如图所示,点P是边长为1的正方形 对角线 上一动点(P与点A、C不重合),点E在 上,且 ,设 , 的面积为y,则下列图象中,能表示y与x函数关系的图象大致是( )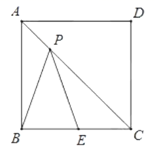 A、
A、 B、
B、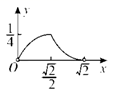 C、
C、 D、
D、
二、填空题
-
11. 若代数式 有意义,则x的取值范围是 .12. 如图,已知四边形 是 的内接四边形,且 是等边三角形, 的半径为2,则劣弧 的长为 .
 13. 如图,将直线y=x向下平移b个单位长度后得到直线l , l与反比例函数y= (x>0)的图象相交于点A , 与x轴相交于点B , 则OA2﹣OB2的值为 .
13. 如图,将直线y=x向下平移b个单位长度后得到直线l , l与反比例函数y= (x>0)的图象相交于点A , 与x轴相交于点B , 则OA2﹣OB2的值为 . 14. 如图,在 中, , , ,点D是边 上的动点,过点D作 于E点.请探究下列问题:(1)若 ,则 ;(2)若 ,设点F是边 上的动点,连接 、 ,以 、 为邻边作平行四边形 ,且使得顶点G恰好落在 边上,则 .
14. 如图,在 中, , , ,点D是边 上的动点,过点D作 于E点.请探究下列问题:(1)若 ,则 ;(2)若 ,设点F是边 上的动点,连接 、 ,以 、 为邻边作平行四边形 ,且使得顶点G恰好落在 边上,则 . 15. 很多代数公式都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式等.
15. 很多代数公式都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式等.(提出问题)如何用表示几何图形面积的方法计算:
(规律探究)观察下面表示几何图形面积的方法:

(解决问题)请用上面表示几何图形面积的方法写出 =(用含n的代数式表示);
(拓展应用)根据以上结论,计算: 的结果为 .
三、解答题
-
16. 计算: .17. 如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系并给出了格点 (顶点为网格线的交点).
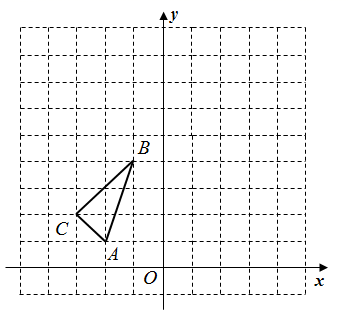 (1)、画出 关于y轴对称的 ;(2)、以点O为位似中心,将 作位似变换得到 ,使得 ,画出位似变换后的 ;(3)、 和 之间的位置关系为 .18. 甲乙两人同驾一辆汽车出游,各匀速驾驶一半路程,共用3小时.到达目的地后,甲对乙说:“我用你所花的时间,可以行使 ”.乙对甲说:“我用你所花的时间,只能行使 ”.试求乙驾车的时长是多少小时.19. 某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1: 3 .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, 3 ≈1.73.)
(1)、画出 关于y轴对称的 ;(2)、以点O为位似中心,将 作位似变换得到 ,使得 ,画出位似变换后的 ;(3)、 和 之间的位置关系为 .18. 甲乙两人同驾一辆汽车出游,各匀速驾驶一半路程,共用3小时.到达目的地后,甲对乙说:“我用你所花的时间,可以行使 ”.乙对甲说:“我用你所花的时间,只能行使 ”.试求乙驾车的时长是多少小时.19. 某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1: 3 .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, 3 ≈1.73.)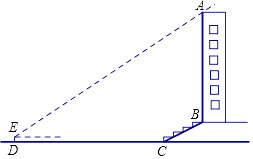 20. 如图,在菱形ABCD中,P为对角线AC上一点,AB与经过A、P、D三点的⊙O相切于点A.
20. 如图,在菱形ABCD中,P为对角线AC上一点,AB与经过A、P、D三点的⊙O相切于点A. (1)、求证:AP=DP;(2)、若AC=8,tan∠BAC= ,求⊙O的半径.21. 为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)、求证:AP=DP;(2)、若AC=8,tan∠BAC= ,求⊙O的半径.21. 为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题: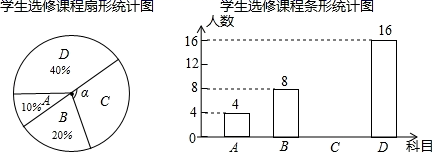 (1)、本次调查的学生共有人;扇形统计图中 度;(2)、请把条形统计图补充完整;(3)、学校为举办2021年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
(1)、本次调查的学生共有人;扇形统计图中 度;(2)、请把条形统计图补充完整;(3)、学校为举办2021年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.

