安徽省合肥市包河区2021年中考数学二模试卷
试卷更新日期:2021-05-21 类型:中考模拟
一、单选题
-
1. 2021的相反数是( )A、 B、 C、2021 D、2. 计算 的结果是( )A、 B、 C、 D、3. 下列几何体中,主视图和左视图都为矩形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列整数中,与 最接近的整数是( )A、3 B、4 C、5 D、65. 一副三角板如图放置,则 的度数为( )
4. 下列整数中,与 最接近的整数是( )A、3 B、4 C、5 D、65. 一副三角板如图放置,则 的度数为( ) A、 B、 C、 D、6. 随着美丽乡村建设和发展,某乡村2019年旅游总收入为a万元,计划到2021年旅游总收入在2019年基础上翻两番.设每年的旅游总收入平均增长率为x,以下方程正确的是( )A、 B、 C、 D、7. 某校团委组织团员开展“百年党史”知识竞赛,九(1)班6位参赛同学成绩为:83,87,80,83,88,83.则以下说法错误的是( )A、6位同学成绩的平均数是84 B、6位同学成绩的众数是83 C、6位同学成绩的方差约为7.3 D、6位同学成绩的中位数是81.58. 已知整数 ,满足条件: ,依次类推 的值为( )A、 B、 C、 D、9. 如图,在 中, ,以 上一点O为圆心作 与 、 都相切, 与 的另一个交点为D,则线段 的长为( )
A、 B、 C、 D、6. 随着美丽乡村建设和发展,某乡村2019年旅游总收入为a万元,计划到2021年旅游总收入在2019年基础上翻两番.设每年的旅游总收入平均增长率为x,以下方程正确的是( )A、 B、 C、 D、7. 某校团委组织团员开展“百年党史”知识竞赛,九(1)班6位参赛同学成绩为:83,87,80,83,88,83.则以下说法错误的是( )A、6位同学成绩的平均数是84 B、6位同学成绩的众数是83 C、6位同学成绩的方差约为7.3 D、6位同学成绩的中位数是81.58. 已知整数 ,满足条件: ,依次类推 的值为( )A、 B、 C、 D、9. 如图,在 中, ,以 上一点O为圆心作 与 、 都相切, 与 的另一个交点为D,则线段 的长为( ) A、 B、 C、 D、110. 已知 中, ,正方形 中, 和 在同一直线上,将 向右平移,则 和正方形 重叠部分的面积y与点B移动的距离x之间的函数图象大致是( )
A、 B、 C、 D、110. 已知 中, ,正方形 中, 和 在同一直线上,将 向右平移,则 和正方形 重叠部分的面积y与点B移动的距离x之间的函数图象大致是( )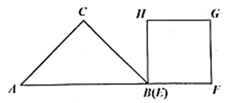 A、
A、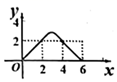 B、
B、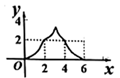 C、
C、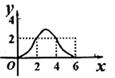 D、
D、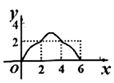
二、填空题
-
11. 因式分解:2y2﹣18= .12. 每到四月,许多地方的杨絮、柳絮如雪花漫天飞舞,人们不堪其忧,据测定,杨絮纤维的直径约为 ,该数值用科学记数法表示为 .13.
如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为 .
 14. 正方形 的边长为8,点E、F分别在边 、 上,将正方形沿 折叠,使点A落在 处,点B落在点 处, 交 于G.以下结论:
14. 正方形 的边长为8,点E、F分别在边 、 上,将正方形沿 折叠,使点A落在 处,点B落在点 处, 交 于G.以下结论:①当 为 中点时, 三边之比为 ;
②当 三边之比为 时, 为 中点;
③当 在 上移动时, 周长不变;
④当 在 上移动时,始终有 .
其中正确的有(写出所有正确结论的序号)

三、解答题
-
15. 解不等式 >x﹣1,并写出它的所有正整数解.16. 甲、乙两个施工队共同完成某区域绿化改造工程,乙队先单独做3天后,再由两队合作7天完成全部工程.已知乙队单独完成此项工程所需天数是甲队单独完成此项工程所需天数的2倍,求甲、乙两个施工队单独完成此项工程各需多少天?17. 如图,是由边长为1的小正方形组成的网格,已知格点正方形 及格点O.
 (1)、将正方形 向左平移2个单位,再向上平移2个单位,得到正方形 ;(2)、以O为位似中心,在点O的同侧画出正方形 的位似图形 ,使位似比为1∶2;(3)、除了点O外,正方形 和正方形 还有位似中心吗?如果有,请找出来.18. 如图,在平面直角坐标系 中,直线 与函数 的图象交于A,B两点,且点A的坐标为 .
(1)、将正方形 向左平移2个单位,再向上平移2个单位,得到正方形 ;(2)、以O为位似中心,在点O的同侧画出正方形 的位似图形 ,使位似比为1∶2;(3)、除了点O外,正方形 和正方形 还有位似中心吗?如果有,请找出来.18. 如图,在平面直角坐标系 中,直线 与函数 的图象交于A,B两点,且点A的坐标为 .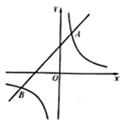 (1)、求a和k的值;(2)、已知点 ,过点P作平行于y轴的直线,交直线 于点C,交函数 的图象于点D.若 ,结合函数的图象,直接写出m的取值范围.19. 如图是某款手机支架摆放手机时的侧面示意图,现测得支撑板 , ,求手机底端E到底座 的距离.(精确到0.1,参考数据: , , , , , , )
(1)、求a和k的值;(2)、已知点 ,过点P作平行于y轴的直线,交直线 于点C,交函数 的图象于点D.若 ,结合函数的图象,直接写出m的取值范围.19. 如图是某款手机支架摆放手机时的侧面示意图,现测得支撑板 , ,求手机底端E到底座 的距离.(精确到0.1,参考数据: , , , , , , ) 20. 将正方形 和等腰 如图所示摆放,正方形的边长为2,将此图剪后拼成一个新的正方形.
20. 将正方形 和等腰 如图所示摆放,正方形的边长为2,将此图剪后拼成一个新的正方形. (1)、新正方形的边长为;(2)、在原图中画出剪拼示意图(保留剪和拼的痕迹);(3)、剪拼过程中, 被分割成两部分,求这两部分的面积比.21. 九年级第一次模拟考试结束后,数学李老师对本班数学成绩作质量分析,并制成如下统计图表,根据图表中信息,解答问题.
(1)、新正方形的边长为;(2)、在原图中画出剪拼示意图(保留剪和拼的痕迹);(3)、剪拼过程中, 被分割成两部分,求这两部分的面积比.21. 九年级第一次模拟考试结束后,数学李老师对本班数学成绩作质量分析,并制成如下统计图表,根据图表中信息,解答问题.一模成绩统计表
等级
分数段
频数
优秀
A:
5
B:
m
良好
C:
n
D:
8
合格
E:
5
F:
3
不合格
G:
2
 (1)、本班共有学生人,表格中 , ;(2)、若全校九年级有学生800人,各班成绩相当,请估计全校达到优秀等级的人数;(3)、成绩最好的5位同学中有3男2女,从他们当中随机选择2位同学进行经验介绍,请用画树状图或列表法求恰好选中1男1女的概率.22. 某超市经销A、B两种商品.商品A每千克成本为20元,经试销发现,该种商品每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价、销售量的对应值如下表所示:
(1)、本班共有学生人,表格中 , ;(2)、若全校九年级有学生800人,各班成绩相当,请估计全校达到优秀等级的人数;(3)、成绩最好的5位同学中有3男2女,从他们当中随机选择2位同学进行经验介绍,请用画树状图或列表法求恰好选中1男1女的概率.22. 某超市经销A、B两种商品.商品A每千克成本为20元,经试销发现,该种商品每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价、销售量的对应值如下表所示:销售单价x(元/千克)
25
30
35
40
销售量y(千克)
50
40
30
20
商品B的成本为6元/千克,销售单价为10元/千克,但每天供货总量只有60千克,且能当天销售完.为了让利消费者,超市开展了“买一送一”活动,即买1千克的商品A,免费送1千克的商品B.
(1)、求y(千克)与x(元千克)之间的函数表达式;(2)、设这两种商品的每天销售总利润为w元,求出w(元)与x的函数关系式;(3)、若商品A的售价不低于成本,不高于成本的180%,当销售单价定为多少时,才能使当天的销售总利润最大?最大利润是多少?(总利润=两种商品的销售总额-两种商品的成本)
23. 在 中, ,垂足为点D,点E为 延长线上一点,且 ,延长 交 于点F. (1)、若 ,请判断 的形状,并给出证明;(2)、若 ,求证: ;(3)、若 ,求 的长.
(1)、若 ,请判断 的形状,并给出证明;(2)、若 ,求证: ;(3)、若 ,求 的长.