吉林省名校调研系列卷2020-2021学年八年级下学期数学期中试卷
试卷更新日期：2021-05-21 类型：期中考试
一、选择题(每小题2分，共12分)
-
1. 计算( )2的结果是 )A、-5 B、5 C、±5 D、252. 若 是最简二次根式，则a的值可能是（ ）A、24 B、16 C、7 D、3. 如图，在△ABC中，AC= 8，DE是△ABC的中位线，则DE的长度是（ ）
A、4 B、5 C、6 D、34. 下列几组数中，不能作为直角三角形三边长的是（ ）A、5，12，13 B、9，40，41 C、3，4，5 D、2，3，45. 已知菱形ABCD的周长为16，则菱形ABCD的边长为（ ）A、4 B、8 C、12 D、26. 如图，在 ABCD中，对角线AC、BD相交于点O，OA=3cm，若要使平行四边形ABCD为矩形，则OB的长度为（ ）
A、4cm B、3cm C、2cm D、1cm二、填空题(每小题3分，共24分)．
-
7. 计算： =8. 与 最接近的整数是9. 在平行四边形ABCD中，若∠A= 38°，则∠C=10. 已知矩形ABCD的面积为 cm2 ， 它的长为2 cm，则它的宽为cm11. 如图，在正方形ABCD中，E为边BC的中点，连接AE，若AB=2，则AE的长为
12. 如图，AC为菱形ABCD的对角线，若∠D=50°，则∠BAC的大小为度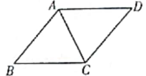
13. 如图，在平面直角坐标系中，点A(-2，4)与点B(-10，0)之间的距离为
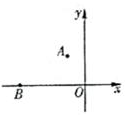14. 如图，点E是 ABCD的边CD的中点，AD、BE的延长线相交于点F，若DF=3，DE=2，则 ABCD的周长为
三、解答题(每小题5分，共20分)
-
15. 计算：16. 计算17. 如图，在Rt△ABC中∠ACB=90°，CD是斜边AB上的中线，AC=4，CD=3。求直角边BC的长
18. 若a、b、c是△ABC的三条边长，且满足等式求证：△ABC是直角三角形
四、解答题(每小题7分，共28分)
-
19. 如图，AC、BD相交于点O，AB∥CD，AD∥BC，E、F分别是OB、OD的中点。求证：四边形AECF是平行四边形
20. 图①、图②均是4×4的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点叫做格点，线段AB的端点均在格点上在给定的网格中按要求画图，使所画图形的顶点均在格点上，不要求写出画法。
(1)、在图①中以AB为一边画一个平行四边形；(2)、在图②中以AB为对角线画一个非正方形的矩形。21. 如图，一根长度为120cm的木棒的两端A、B系者一根长度为180cm的绳子，现准备在绳子上找一点C，然后将绳子拉直。使拉直后的绳子与木棒构成一个直角三角形。且AB为直角边，求这个点将绳子分成的两段各有多长？
22. 如图，菱形ABCD的对角线AC、BD相交于点O，分别过A、D两点作AO、DO的垂线，两垂线交于点E。
(1)、求证：四边形AODE是矩形；(2)、若∠DAE=60°，AD=6，求BD的长。五、解答题(每小题8分，共16分}
-
23. 某中学有一块四边形的空地ABCD，如图，学校计划在空地上种植草皮，经测量∠B=90°，AB=3m，BC=4m，CD=12m，AD=13m。若每平方米草皮需费200元，问学校需要投入多少资金买草皮？
24. 如图，在 ABCD中，点E在BC的延长线上，EC=BC，连接DE、AC，AC⊥AD于点A
(1)、求证：四边形ACED是矩形；(2)、连接BD，交AC于点F，若AC=2AD，求∠BDE的度数。六、解答题(每小题10分，共20分)次正
-
25. 如图，在正方形ABCD中，E是边AB上的点，连接CE，过点D作DF⊥CE，分别交BC、CE于点F、G
(1)、求证：CE=DF；(2)、若AB=3，图中阴影部分的面积和与正方形ABCD的面积之比为2：3，则△DCG的面积为 ， CG+DG的长为26. 如图，在矩形ABCD中，AB =2，E、F分别是边BC，AD上的点，连接EF，将四边形CEFD沿EF折叠，C、D的对应点分别为点G、H，EG交边AD于点M，延长HF交边BC于点N
(1)、求证：四边形EMFN是菱形；(2)、若FN⊥BC，直接写出四边形EMFN的一条对角线的长；(3)、若EF=MF，求EN的长