广东省广州市增城区2020-2021学年八年级下学期数学期中试卷
试卷更新日期:2021-05-21 类型:期中考试
一、选择题(共10小题,每小题3分,满分30分)
-
1. 下列各式中,属于最简二次根式的是( )A、 B、 C、 D、2. 下列各组数中,能构成直角三角形的一组是( )A、1,2,3 B、1,1, C、2,3,4 D、7,15,173. 如图,在 ABCD中,AB=5,AD=7,则 ABCD的周长为( )
 A、12 B、14 C、35 D、244. 下列各图中,不能表示y是x的函数的是( )A、
A、12 B、14 C、35 D、244. 下列各图中,不能表示y是x的函数的是( )A、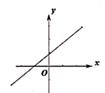 B、
B、 C、
C、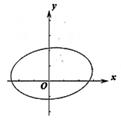 D、
D、 5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,数轴上点A表示的数为a,则a的值是( )
5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,数轴上点A表示的数为a,则a的值是( ) A、 +1 B、1- C、 -1 D、7. 下列命题中,属于假命题的是( )A、相等的角是对顶角 B、两直线平行,同旁内角互补 C、平行四边形的对角线互相平分 D、矩形的对角线相等8. 化简| -3|的结果为( )A、 -3 B、- -3 C、3+ D、3-9. 如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE的长为( )
A、 +1 B、1- C、 -1 D、7. 下列命题中,属于假命题的是( )A、相等的角是对顶角 B、两直线平行,同旁内角互补 C、平行四边形的对角线互相平分 D、矩形的对角线相等8. 化简| -3|的结果为( )A、 -3 B、- -3 C、3+ D、3-9. 如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE的长为( ) A、10 B、8 C、6 D、410. 如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是( )
A、10 B、8 C、6 D、410. 如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是( )
①OG= AB ;②与△DEG全等的三角形共有5个;③四边形ODEG与四边形OBAG面积相等;④由点A、B、D、E构成的四边形是菱形
A、①③④ B、①④ C、①②③ D、②③④二、填空题(共6小题,每小题3分,满分18分)
-
11. 函数y= 的自变量x取值范围是12. 命题“同位角相等,两直线平行”的逆命题是: .13. 市场上一种豆子的单价是2元/千克,豆子总的售价y (元)与所售豆子的重量x (千克)之间的函数关系式为14. 如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、AC、AD的中点,EF=3,则AB的长度为
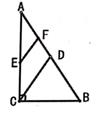 15. 如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,则∠E=
15. 如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,则∠E= 16. 如图,四边形ABCD为菱形,AB=2,∠BCD=30°,点E在CD延长线上,且CD=DE,∠E=45°,点H是AC上的一个动点,则HD+HE的最小值为
16. 如图,四边形ABCD为菱形,AB=2,∠BCD=30°,点E在CD延长线上,且CD=DE,∠E=45°,点H是AC上的一个动点,则HD+HE的最小值为
三、解答题:(本题有9个小题,共72分.)
-
17. 计算18. 如图,在Rt△ABC中,∠B=90°,∠C=30°,AB=4,求BC的长
 19. 如图,在 ABCD中,点E、F分别是AD、BC上的点,且AE=CF
19. 如图,在 ABCD中,点E、F分别是AD、BC上的点,且AE=CF求证:四边形BEDF为平行四边形
 20. 先化简再求值:
20. 先化简再求值:,其中a= ,b=
21. 如图,四边形ABCD中,∠B=90°,AB=4,BC=3,CD=12,AD=13,求这个四边形ABCD的面积 22. 某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图是王老师从家到学校这一过程行驶路程s (千米)与时间t (分)之间的关系。
22. 某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图是王老师从家到学校这一过程行驶路程s (千米)与时间t (分)之间的关系。 (1)、学校离王老师家多远?从出发到学校用了多少时间?(2)、王老师吃早餐用了多少时间?(3)、王老师吃早餐之前的速度快还是吃完早餐之后的速度快?23. 如图,将矩形ABCD沿对角线AC折叠,使点B落到点B'的位置,AB'与CD交于点E。
(1)、学校离王老师家多远?从出发到学校用了多少时间?(2)、王老师吃早餐用了多少时间?(3)、王老师吃早餐之前的速度快还是吃完早餐之后的速度快?23. 如图,将矩形ABCD沿对角线AC折叠,使点B落到点B'的位置,AB'与CD交于点E。 (1)、求证:△ADE≌ △CBE;(2)、若AB=8,DE=3,点P为线段AC的任意一点,PG⊥AE于G,PH⊥DC于H,求PG+PH的值。24. 如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度。
(1)、求证:△ADE≌ △CBE;(2)、若AB=8,DE=3,点P为线段AC的任意一点,PG⊥AE于G,PH⊥DC于H,求PG+PH的值。24. 如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度。 (1)、当t=2秒时,求AD的长;(2)、在D运动过程中,△CBD能否为直角三角形,若不能,说明理由,若能,请求出t的值。25. 如图①,四边形ABCD是正方形,E是对角线BD上一点,连接AE、CE
(1)、当t=2秒时,求AD的长;(2)、在D运动过程中,△CBD能否为直角三角形,若不能,说明理由,若能,请求出t的值。25. 如图①,四边形ABCD是正方形,E是对角线BD上一点,连接AE、CE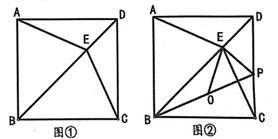 (1)、求证:AE=CE;(2)、如图②,点P是边CD上的一点,且PE⊥BD于E,连接BP,点O为BP的中点,连接OE。若∠PBC=30°,求∠POE的度数;(3)、在(2)的条件下,若OE= ,求CE的长。
(1)、求证:AE=CE;(2)、如图②,点P是边CD上的一点,且PE⊥BD于E,连接BP,点O为BP的中点,连接OE。若∠PBC=30°,求∠POE的度数;(3)、在(2)的条件下,若OE= ,求CE的长。