山西省运城市2020-2021学年七年级下学期数学期中试卷

试卷更新日期：2021-05-21 类型：期中考试

进入出卷网下载

一、选择题(本大题共10个小题，每小题3分，共30分．)

1. 若代数式 $\sqrt{8 - 2 x}$ 有意义，则实数x的取值范围是：（）

A、x≤-4 B、x≤4 C、x≥4 D、x≥-4

查看试题解析
2. 如图，将 $▱$ ABCD的一边BC延长至点E，若∠1=80°，则∠A等于（）

A、80° B、120° C、100° D、110°

查看试题解析
3. 已知△ABC三边长分别为a，b，c，且满足 $\sqrt{a - 1} + | b - \sqrt{2} | + {(c - \sqrt{3})}^{2}$ =0，则△ABC是（）

A、以c为斜边长的直角三角形 B、以b为斜边长的直角三角形 C、以a为斜边长的直角三角形 D、等腰三角形

查看试题解析
4. 下列二次根式中，与 $\sqrt{24}$ 可以合并的是（）

A、 $\sqrt{54}$ B、 $\sqrt{48}$ C、 $\sqrt{30}$ D、 $\sqrt{18}$

查看试题解析
5. 直角三角形两直角边长分别为6和8，则此三角形斜边上的中线的长是（）

A、10 B、5 C、4 D、3

查看试题解析
6. 下列二次根式的运算中正确的是（）

A、 $\sqrt{5} - \sqrt{2} = \sqrt{3}$ B、 $\sqrt{6} + \sqrt{3} = 3$ C、 $\sqrt{4} \div \sqrt{2} = 2$ D、 $\sqrt{3} \times \sqrt{\frac{1}{3}} = 1$

查看试题解析
7. 若 $\sqrt{{(4 - 2 b)}^{2}}$ =2b-4，则（）

A、b>2 B、b<2 C、b≥2 D、b≤2

查看试题解析
8. 如图，两条笔直的公路l₁ ， l₂相交于点A，村庄C的村民在公路的旁边建了两个加工厂B和D，已知AB=BC=CD=DA=5公里，村庄C到公路l₁的距离为4公里，则村庄C到公路l₂的距离是（）

A、3公里 B、4公里 C、5公里 D、6公里

查看试题解析
9. 为了研究特殊四边形，刘老师制作了这样一个教具(如图1)：用钉子将四根木条钉成一个平行四边形框架ABCD，并在A与C，B与D两点之间分别用一根橡皮筋拉直固定，课上，刘老师右手拿住木条BC，用左手向右推动框架至AB⊥BC(如图2)，观察所得到的四边形，下列结论正确的有（）

①∠BCA= 45°；②AC的长度变小；③AC= BD；④AC⊥BD

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，在正方形ABCD中，取AD的中点E，连接EB，延长DA至F，使EF=EB，以线段AF为边作正方形AFGH，交AB于点H，则 $\frac{A B}{A H}$ 的值是（）

A、 $\frac{3}{2}$ B、 $\frac{\sqrt{3} + 1}{2}$ C、 $\frac{\sqrt{5} - 1}{2}$ D、 $\frac{\sqrt{5} + 1}{2}$

查看试题解析

二、填空题(本大题共5个小题，每小题3分，共15分)

11. 化简： $\sqrt{8}$ =

查看试题解析
12. 如图，D，E，F分别为△ABC各边的中点，则图中的平行四边形有个

查看试题解析
13. 如图，在同一平面内， $▱$ ABCD与 $▱$ DCFE的周长相等，且∠BAD=60°，F=110°，则∠DAE的度数为

查看试题解析
14. 如图，一只蚂蚁从长为7cm、宽为5cm、高为9cm的长方体纸箱的A点沿纸箱表面爬到B点，那么它所走的最短路线的长是

查看试题解析
15. 过△ABC的顶点C画线段CD，使得线段CD与AB边平行且相等，则下列说法：
①若∠BAC=90°，则以A，B，C，D为顶点的四边形是矩形；

②若以A，B，C，D为顶点的四边形是矩形，则∠BAC= 90°；

③若AB=AC= BC，则以A，B，C，D为顶点的四边形是菱形；

④若以A，B，C，D为顶点的四边形是菱形，则AB=AC。

其中正确的说法有(填序号)

查看试题解析

三、解答题(本大题共8个小题，共75分．)

16. (本题共2小题，每小题5分，共10分)
计算：

(1)、 $\sqrt{72} + \frac{9}{2} \sqrt{2} - 2 \sqrt{18}$

(2)、 $(\sqrt{5} + 2) (\sqrt{5} - 2) - {(\sqrt{3} - 2)}^{2}$

查看试题解析
17. 如图，在平行四边形ABCD中，AB= $\sqrt{12}$ ，BC= $\sqrt{27}$ ，边AD与BC之间的距离为 $\sqrt{10}$ ，求AB与CD间的距离．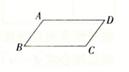

查看试题解析
18. 如图，∠AOB=90°，OA=45cm，OB=15cm，一个小球从点A出发沿着AO方向匀速前进向点O滚动，一个机器人同时从点B出发，沿直线匀速行走去截小球，在点C处截住了小球，如果小球滚动的速度与机器人行走的速度相等，求机器人行走的路程BC。

查看试题解析
19. 如图，点B、E分别在AC，DF上，AF分别交BD，CE于点M、N，∠A=∠F，∠C=∠D。

(1)、求证：四边形BCED是平行四边形。

(2)、已知DE=3，连接BN，若BN平分∠(DBC，求CN的长。

查看试题解析
20. 在平面直角坐标系中，已知两点的坐标是P(x₁ ， y₁)，Q(x₂ ， y₂)，则P，Q两点之间的距离可以用公式d= $\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ 计算。阅读以上内容并解答下列问题：

(1)、已知点M(2，4)，N(-3，-8)，则M，N两点之间的距离为；

(2)、若点A(3，4)，B(-4，3)，点O是坐标原点，判断△AOB是什么三角形，并说明理由。

查看试题解析
21. 在边长为3的正方形ABCD中，点E在边CD所在直线上，连接BE，以BE为边，在BE的下方作正方形BEFG，并连接AG。

(1)、如图1，当点E与点D重合时，BG=；AG=；

(2)、如图2，当点E在线段CD上时，DE=1，求AG的长。

查看试题解析
22. 综合与实践
如图，四边形ABCD是菱形，点H为对角线AC的中点，点E在AB的延长线上，CE⊥AB，垂足为E，点F在AD的延长线上，CF⊥AD，垂足为F。

(1)、若∠BAD=60°，判断四边形CEHF的形状并证明。

(2)、若CE=4，AE=8，求菱形ABCD的面积。

查看试题解析
23. 综合与探究
如图，在矩形ABCD中，E是AD的中点，将△ABE沿BE折叠，点A的对应点为点F。

(1)、如图1，当点F恰好落在BC边上时，判断四边形ABFE的形状，并说明理由。

(2)、如图2，当点F在矩形ABCD内部时，延长BF交DC边于点G。
①试探究线段BG，AB，DG之间的数量关系，并说明理由。

②当G点分CD边的比为1：3时，试探究矩形ABCD的边长AD和AB之间的数量关系，并说明理由。

查看试题解析