吉林省名校调研系列卷2020-2021学年八年级下学期数学期中试卷
试卷更新日期：2021-05-21 类型：期中考试
一、选择题(每小题2分，共12分)
-
1. 9的算术平方根是（ ）A、3 B、-3 C、9 D、812. 在平面直角坐标系中，下列各点位于第三象限的是（ ）A、(0，3) B、(-2，1) C、(1，-2) D、(-1，-1)3. 如图，已知直线AB、CD被直线ED所截，AB∥CD，若∠D=40°，则∠1等于（ ）
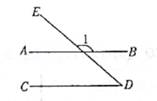A、140° B、130° C、120° D、100°4. 在下列各数中，是无理数的是（ ）A、0.12 B、 C、 D、5. 如图是一所学校的部分平面示意图，在同一平面直角坐标系中。若体育馆A的坐标为(-2，5)，科技馆B的坐标为(-5，2)，则教学楼C的坐标为（ ）
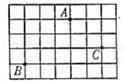A、(0，3) B、(-1，-3) C、(3，0) D、(-2，0)6. 如图，下列条件中能判定AB∥CD的是（ ）
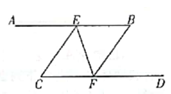A、∠AEC=∠BFD B、∠CEF=∠BFE C、∠AEF+∠CFE=180° D、∠C=∠BFD二、填空题(每小题3分，共24分)
-
7. -0.001的立方根是_。8. 如图，将木条a、b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a转动的度数至少是度。
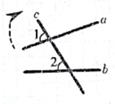9. 在平面直角坐标系中，将点A(9，-7)向左平移2个单位长度，则平移后对应的点A‘的坐标是。10. 如图，在数轴上，点B与点A到原点的距离相等，则点B表示的实数是。
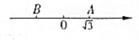11. 下列命题中：①对顶角相等；②同位角相等；③平行于同一条直线的两条直线平行；④若a2>b2 ， 则a>b，是真命题的是。(填序号)12. 若一个正数的两个不同的平方根分别是5和3m+1，则m=13. 如图，在平面直角坐标系中，AB平行于x轴，点A的坐标为(4，3)，点B在点A的左侧，AB=a，若点B在第二象限，则a的取值范围是
14. 如图，已知AD∥BE，点C是线段FG上的动点，若在点C移动的过程中，存在某时刻使得∠ACB=45°，∠DAC=22，则∠EBC=度。
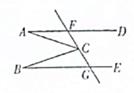
三、解答题(每小题5分，共20分)
-
15. 计算：|-3|-(-1)+ -16. 如图，图中每个小正方形的边长均为1，已知极地动物馆的坐标为(5，4)，孔雀园的坐标为(6，-1)，先建立平面直角坐标系。再表示其他三个景点的坐标。
17. 如图，直线AB，CD相交于点O，过点O作OE⊥AB，OF平分∠BOD。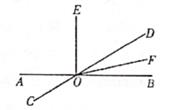
(1)、直接写出∠AOC的补角；(2)、若∠AOC=40°，求∠EOF的度数。18. 求下列各式中x的值(1)、25x2=169；(2)、x3-4= 60四、解答题(每小题7分，共28分}
-
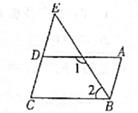
19. 已知4x-3的算术平方根是1，2x+y-6的立方根是2。(1)、求x、y的值；(2)、求3xy的平方根。20. 如图，已知∠A=∠C，∠1+∠2=180°，试猜想AB与CD之间有怎样的位置关系？并说明理由，请你将下列证明过程补充完整．
结论：AB∥CD．
证明：∵∠1+∠2=180°(已知)，
∴AD∥ ▲ （ ▲ ）
∴∠ ▲ =∠ ▲ (两直线平行，同位角相等)．
又∵∠A=∠C(已知)，
∴∠ ▲ =∠ ▲ (等量代换)，
∴AB∥CD( ▲ )
21. 小明想用一块面积为400平方厘米的正方形纸片，沿着边的方向，裁出一块面积为360平方厘米的长方形纸片，使它的长与宽之比为4：3，小明不知道能否裁得出米，聪明的你帮他想想，他能裁得出来吗(通过计算说明)？22. 如图，在平面直角坐标系中，已知点A(-3，3)、B(-5，1)，C(-2，0)，P(a，b)是三角形ABC的边AC上的任意一点，三角形ABC经过平移后得到三角形A1B1C1 ， 点P的对应点为P1(a+6，b-2)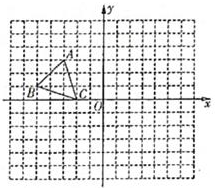
(1)、直接写出点A1、B1、C1的坐标(点A、B、C的对应点分别为A1、B1、C1)；(2)、在图中画出三角形A1B1C1五、解答题(每小题8分，共16分)
-
23. 如图，已知AB∥CD，AC平分∠DAB，且∠DCA=28°，∠B=96°。
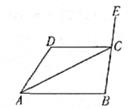(1)、求∠DCE的度数；(2)、求∠D的度数。24. 在平面直角坐标系中，已知点M(a-6，5a+10)。(1)、若点M在y轴上，求a的值；(2)、若点M到x轴的距离为5，求点M的坐标；(3)、若点M在过点A(2，-4)且与y轴平行的直线上，求点M的坐标。六、解答题(每小题10分，共20分)
-
25. 对于一个实数m(m为非负实数)；规定其整数部分为日小数部分为b，例如：当m=3时，则a= 3，b=0；当m=4.5时，则a=4，b=0.5，(1)、当m=π时，b=；当m= 时，a=；(2)、若a=5，b=6- ，则m=(3)、当m=9+ 时，求a-b的值。26. 如图，在平面直角坐标系中，已知A(0，a)、B(b，0)、C(3，c)三点，其中a、b、c满足|a-2|+(b-3)2+ =0；
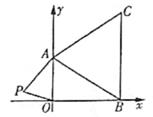(1)、求a、b、c的值；(2)、若在第二象限内有一点P(m， )，请用含m的式子表示四边形ABOP的面积；(3)、在(2)的条件下，是否存在点P，使四边形ABOP的面积为三角形ABC的面积的2倍？若存在，直接写出点P的坐标，若不存在，请说明理由。