初中数学苏科版八年级下册第九章 中心对称图形 单元测试卷
试卷更新日期：2021-05-21 类型：单元试卷
一、单选题
-
1. 下列图形中，既是轴对称图形又是中心对称图形的有（ ）
A、4个 B、3个 C、2个 D、1个2. 下列命题是假命题的是（ ）A、对角线互相平分的四边形是平行四边形 B、对角线相等的平行四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分且相等的四边形是正方形3. 如图，在△ABC中，∠BAC＝105º，将△ABC绕点A按逆时针方向旋转得到△ADE，若点D恰好落在边BC上，且AD＝CD，则∠C的度数为（ ）
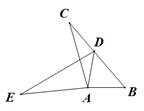A、25º B、30º C、35º D、40º4. 如图，平行四边形ABCD的对角线AC与BD相交于点O ， AE⊥BC ， 垂足为E ， ，AC＝2，BD＝4，则AE的长为（ ）
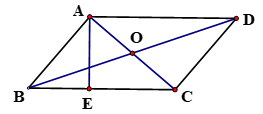A、 B、 C、 D、5. 如图，在平行四边形 中，点A1 ， A2 ， A3 ， A4和C1 ， C2 ， C3 ， C4分别是AB和CD的五等分点，点B1 ， B2和D1 ， D2分别是BC和DA的三等分点，已知四边形A4B2C4D2的面积为2，则平行四边形ABCD的面积为（ ）
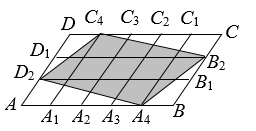A、4 B、 C、 D、306. 如图，菱形ABCD的边长是4cm，且∠ABC＝60°，E是BC中点，P点在BD上，则PE+PC的最小值为（ ）cm.
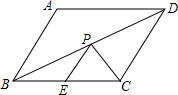A、2 B、2 C、3 D、47. 如图，在△ABC中，∠ACB＝90°，以△ABC的各边为边作三个正方形，点G落在HI上，若AC＋BC＝6，空白部分面积为10.5，则AB的长为（ ）
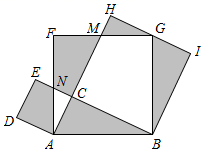A、3 B、 C、2 D、8. 如图，已知▱OABC的顶点A，C分别在直线 和 上，O是坐标原点，则对角线OB长的最小值为（ ）
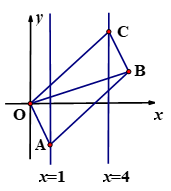A、3 B、4 C、5 D、69. 矩形ABCD与ECFG如图放置，点B ， C ， F共线，点C ， E ， D共线，连接AG ， 取AG的中点H，连接EH ． 若 ， ，则 （ ）
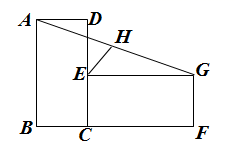A、 B、2 C、 D、10. 如图，正方形 的面积为 ， 是等边三角形，点 在正方形 内，在对角线 上有一点 ，使 的和最小，则这个最小值为（ ）．
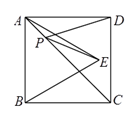A、 B、 C、 D、二、填空题
-
11. 如图， 按顺时针方向转动40°得 ，点D恰好在边BC上，则∠C＝°.
12. 如图，在平行四边形 中， 、 相交于点 ，点 是 的中点.若 ，则 的长是 .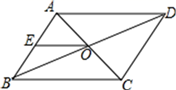
13. 在平面直角坐标系 中，已知点 ， ，请确定点C的坐标，使得以A ， B ， C ， O为顶点的四边形是平行四边形，则满足条件的所有点C的坐标是 ．14. 如图，在菱形ABCD中，对角线AC、BD交于点O，过点A作AM⊥CD于点M，已知AC＝6，BD＝8，则AM＝.
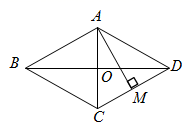15. 如图，□ 的周长为 ， 相交于点 ， 交 于 ，则 的周长为 .
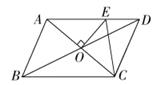16. 如图，在长方形ABCD中，AB＝12，BC＝9，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE＝OD，则AP＝.
17. 如图，△ABC中，AB＝4，AC＝3，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，则线段EF的长为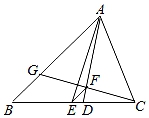
18. 如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与点B，C重合），过点C作CN⊥DM交AB于点N，连结OM、ON，MN．下列五个结论：①△CNB≌△DMC；②ON＝OM；③ON⊥OM；④若AB＝2，则S△OMN的最小值是1；⑤AN2+CM2＝MN2 ． 其中正确结论是；（只填序号）
三、综合题
-
19. 在下列网格图中，每个小正方形的边长均为1个单位．在Rt△ABC中，∠C＝90°，AC＝3，BC＝4．
（1）试在图中做出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△A1B1C1；
（2）若点B的坐标为（﹣3，5），试在图中画出直角坐标系，并写出 A、C两点的坐标；
（3）根据（2）的坐标系作出与△ABC关于原点对称的图形△A2B2C2 ， 并写出B2、C2两点的坐标．20. 如图，四边形ABCD是平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E.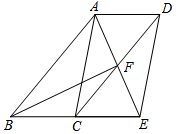
(1)、求证：BE＝CD；(2)、若BF恰好平分∠ABE，连接AC、DE，求证：四边形ACED是平行四边形.21. 如图，在Rt ABC中，∠ACB＝90°．过点C的直线m∥AB，D为AB边上一点，过点D作DE⊥BC交直线m于点E，垂足为点F，连结CD、BE．
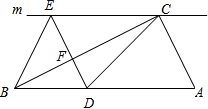(1)、求证：CE＝AD(2)、当点D是AB中点时，四边形BECD是什么特殊四边形？说明你的理由；(3)、若点D是AB中点，当四边形BECD是正方形时，则∠A大小满足什么条件？22. 如图①，在矩形OACB中，点A、B分别在x轴、y轴正半轴上，点C在第一象限，OA＝8，OB＝6．
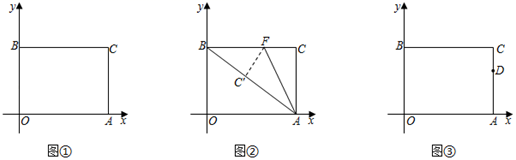(1)、请直接写出点C的坐标；(2)、如图②，点F在BC上，连接AF，把 ACF沿着AF折叠，点C刚好与线段AB上一点 重合，求线段CF的长度；(3)、如图③，动点P(x，y)在第一象限，且y＝2x﹣6，点D在线段AC上，是否存在直角顶点为P的等腰直角 BDP，若存在，请求出点P的坐标；若不存在，请说明理由．23. △ABC中，点O是AC上一动点，过点O作直线MN BC，若MN交∠BCA的平分线于点E，交∠DCA的平分线于点F，连接AE、AF.
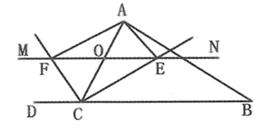(1)、说明： ；(2)、当点O运动到AC中点处时，求证：四边形AECF是矩形；(3)、在（2）的条件下，当△ABC满足什么条件时，四边形AECF为正方形，并加以证明.24. 已知：如图已知直线 的函数解析式为 ，与x轴交于点A，与y轴交于点B．
(1)、求A、B两点的坐标；(2)、若点 为线段 上的一个动点（与A、B不重合），作 轴于点E， 轴于点F，连接 ，问：①若 的面积为S，求S关于m的函数关系式，并写出m的取值范围；
②是否存在点P，使 的值最小？若存在，求出 的最小值；若不存在，请说明理由．
25. 已知四边形ABCD为矩形，对角线AC、BD相交于点O，∠CDO＝30°．点E、F为矩形边上的两个动点，且∠EOF＝60°．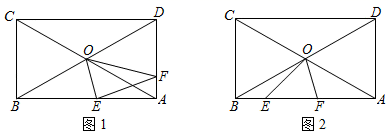
(1)、如图1，当点E、F分别位于AB、AD边上时．①求证：∠DOF＝∠AOE；
②若∠OEB＝75°，求证：DF＝AE．
(2)、如图2，当点E、F同时位于AB边上时，若∠OFB＝75°，试探究线段AF与线段BE的数量关系，并说明理由．26. 如图，四边形ABCD、BEFG均为正方形，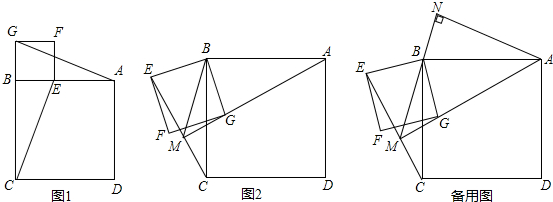
(1)、如图1，连接AG、CE，试判断AG和CE的数量和位置关系并证明.(2)、将正方形BEFG绕点B顺时针旋转β角（0°＜β＜180°），如图2，连接AG、CE相交于点M，连接MB，当角β发生变化时，∠EMB的度数是否发生变化？若不变化，求出∠EMB的度数；若发生变化，请说明理由.(3)、在（2）的条件下，过点A作AN⊥MB交MB的延长线于点N，请直接写出线段CM与BN的数量关系.