湖南省娄底市2019-2020学年高一下学期数学期末考试试卷

试卷更新日期：2021-05-20 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x \in Z | - 1 < x < 5}, B = {x | - 2 ⩽ x \leq 2}$ ，则 $A \cap B =$ （）

A、 ${0, 1, 2}$ B、 ${0, 1}$ C、 ${x | - 1 < x \leq 2}$ D、 $〈 x | - 2 \leq x < 5 〉$

查看试题解析
2. 下列各组函数是同一函数的是（）

A、 $y = \frac{| x |}{x}$ 与y＝1 B、 $y = \frac{x^{2}}{x}$ 与 y＝x C、 $y = \frac{x^{3} + x}{x^{2} + 1}$ 与 y＝x D、 $y = \sqrt{{(x - 1)}^{2}}$ 与 y＝x﹣1

查看试题解析
3. 有20位同学，编号从1至20，现在从中抽取4人作问卷调查，用系统抽样方法确定所抽的编号为（）

A、2，6，10，14 B、5，10，15，20 C、2，4，6，8 D、5，8，11，14

查看试题解析
4. 下列化简正确的是（）

A、 $\cos 82^{\circ} \sin 52^{\circ} - \sin 82^{\circ} \cos 52^{\circ} = \frac{1}{2}$ B、 $\sin 15^{\circ} \sin 30^{\circ} \sin 75^{\circ} = \frac{1}{4}$ C、 $\frac{\tan 48^{\circ} + \tan 72^{\circ}}{1 - \tan 48^{\circ} \tan 72^{\circ}} = - \sqrt{3}$ D、 $\cos^{2} 15^{\circ} + \sin^{2} 15^{\circ} = - \frac{\sqrt{3}}{2}$

查看试题解析
5. 从一批产品中取出三件产品，设事件A为“三件产品全不是次品”，事件B为“三件产品全是次品”，事件C为“三件产品至少有一件是次品”，则下列结论正确的是（）

A、B与C互斥 B、任何两个均互斥 C、A与C互斥 D、任何两个均不互斥

查看试题解析
6. 已知曲线 $C_{1} ： y = \sin x$ ， $C_{2} ： y = \sin (2 x + \frac{π}{3})$ ，则下面结论正确的是（）

A、把 $C_{1}$ 上各点的横坐标伸长到原来的2倍，纵坐标不变，再向左平移 $\frac{π}{6}$ 个单位长度，得到曲线 $C_{2}$ . B、把 $C_{1}$ 上各点的横坐标伸长到原来的2倍，纵坐标不变，再向左平移 $\frac{π}{3}$ 个单位长度，得到曲线 $C_{2}$ . C、把 $C_{1}$ 上各点的横坐标缩短到原来的 $\frac{1}{2}$ 倍，纵坐标不变，再向左平移 $\frac{π}{3}$ 个单位长度，得到曲线 $C_{2}$ . D、把 $C_{1}$ 上各点的横坐标缩短到原来的 $\frac{1}{2}$ 倍，纵坐标不变，再向左平移 $\frac{π}{6}$ 个单位长度，得到曲线 $C_{2}$ .

查看试题解析
7. 已知 $\cos (\frac{π}{6} - α) = \frac{2}{3}$ ，则 $\cos (\frac{5 π}{3} + 2 α)$ 的值为（）

A、 $\frac{5}{9}$ B、 $\frac{1}{9}$ C、 $- \frac{1}{9}$ D、 $- \frac{5}{9}$

查看试题解析
8. 已知向量 $\vec{a} = (- 1, 2)$ ， $\vec{b} = (3, 1)$ ， $\vec{c} = (k, 4)$ ，且 $(\vec{a} - \vec{b}) ⊥ \vec{c}$ ，则k=（）

A、-6 B、-1 C、1 D、6

查看试题解析
9. 已知向量 $\overset{⇀}{a} = (\cos θ ， \sin θ)$ ，向量 $\overset{⇀}{b} = (\sqrt{3} ， - 1)$ ，则 $| 2 \overset{⇀}{a} - \overset{⇀}{b} |$ 的最大值，最小值分别是（）

A、 $4 \sqrt{2}$ ，0 B、4， $4 \sqrt{2}$ C、16，0 D、4，0

查看试题解析
10. 袋中装有外形相同的四个小球，四个球上分别标有2，3，4，6四个数，现从袋中随机取出两个球，则两球上数字之差的绝对值不小于2的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{5}{6}$

查看试题解析
11. 已知点 $M$ 是直线 $3 x + 4 y - 2 = 0$ 上的动点，点 $N$ 为圆 ${(x + 1)}^{2} + {(y + 1)}^{2} = 1$ 上的动点，则 $| M N |$ 的最小值为（）

A、 $\frac{4}{5}$ B、1 C、 $\frac{9}{5}$ D、 $\frac{13}{5}$

查看试题解析
12. 已知函数 $f (x) = \ln | x |$ ， $g (x) = m x^{2}$ ，若方程 $f (x) - g (x) = 0$ 在 $x \in (- \infty ， - 1] \cup [1 ， + \infty)$ 有四个不同的解，则 $m$ 的取值范围为（）

A、 $(0 ， \frac{1}{2 e})$ B、 $(\frac{1}{2 e} ， + \infty)$ C、 $(0 ， \frac{1}{e})$ D、 $(\frac{1}{e} ， + \infty)$

查看试题解析

二、填空题

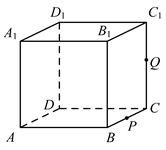
13. 从2个男生、3个女生中随机抽取2人，则抽中的2人不全是女生的概率是.

查看试题解析
14. 已知| $\vec{a}$ |＝2| $\vec{b}$ |，| $\vec{b}$ |≠0，且关于x的方程x²+| $\vec{a}$ |x $- \vec{a} \cdot \vec{b} =$ 0有两相等实根，则向量 $\vec{a}$ 与 $\vec{b}$ 的夹角是．

查看试题解析
15. 已知函数 $f (x)$ 是定义在（-2，2）上的奇函数且是减函数，若 $f (m - 1) + f (1 - 2 m) \geq 0$ ，则实数 $m$ 的取值范围是．

查看试题解析
16. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，P为BC的中点，Q为线段 $C C_{1}$ 上的动点，过点A，P，Q的平面截该正方体所得的截面记为S.则下列命题正确的是（写出所有正确命题的编号）. ①当 $0 < C Q < \frac{1}{2}$ 时，S为四边形；②当 $C Q = \frac{1}{2}$ 时，S为等腰梯形；③当 $C Q = \frac{3}{4}$ 时，S与 $C_{1} D_{1}$ 的交点R满足 $C_{1} R_{1} = \frac{1}{3}$ ；④当 $\frac{3}{4} < C Q < 1$ 时，S为六边形；⑤当 $C Q = 1$ 时，S的面积为 $\frac{\sqrt{6}}{2}$ .

查看试题解析

三、解答题

17. 已知 $| \vec{a} | = 1, | \vec{b} | = \sqrt{2}$ ， $\vec{a}$ 与 $\vec{b}$ 的夹角为 $θ$ .

(1)、若 $\vec{a} / / \vec{b}$ ，求 $\vec{a} \cdot \vec{b}$ ；

(2)、若 $\vec{a} - \vec{b}$ 与 $\vec{a}$ 垂直，求 $θ$ .

查看试题解析
18. 已知函数 $f (x) = \cos x \sin (x - \frac{π}{3}) + \frac{\sqrt{3}}{4}$ $(x \in R)$ .

(1)、求 $f (x)$ 的最小正周期及单调递增区间；

(2)、求 $f (x)$ 在区间 $[- \frac{π}{4} ， \frac{π}{4}]$ 上的最大值和最小值．

查看试题解析
19. 某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六组[90，100），[100，110），…，[140，150]后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：

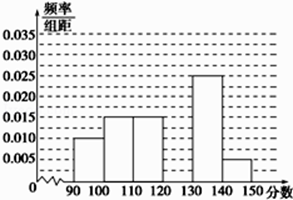(1)、求分数在[120，130）内的频率；

(2)、若在同一组数据中，将该组区间的中点值（如：组区间[100，110）的中点值为 $\frac{100 + 110}{2}$ =105）作为这组数据的平均分，据此，估计本次考试的平均分；

(3)、用分层抽样的方法在分数段为[110，130）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2人，求至多有1人在分数段[120，130）内的概率．

查看试题解析
20. 如图，四棱锥S﹣ABCD中，M是SB的中点，AB∥CD，BC⊥CD，且AB＝BC＝2，CD＝SD＝1，又SD⊥面SAB．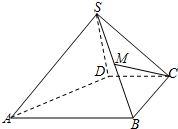

(1)、证明：CD⊥SD；

(2)、证明：CM∥面SAD；

(3)、求四棱锥S﹣ABCD的体积．

查看试题解析
21. 已知直线l:x-y+2=0和圆 $C : x^{2} + y^{2} - 6 y + 5 = 0$

(1)、直线l交圆C于A，B两点，求弦长 $| A B |$ ;

(2)、求过点 $P (2, - 5)$ 的圆的切线方程.

查看试题解析
22. 某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元.设该公司的仪器月产量为 $x$ 台，当月产量不超过400台时，总收益为 $400 x - \frac{1}{2} x^{2}$ 元，当月产量超过400台时，总收益为 $80000$ 元.（注：总收益=总成本+利润）

(1)、将利润表示为月产量 $x$ 的函数 $f (x)$ ；

(2)、当月产量为何值时，公司所获利润最大？最大利润为多少元？

查看试题解析