浙江省五校2021届高三下学期数学5月联考试卷
试卷更新日期:2021-05-18 类型:高考模拟
一、单选题
-
1. 已知全集U={1,2,3,4,5},A={1,3},则 ( )
A、 B、{1,3} C、{2,4,5} D、{1,2,3,4,5}2. 已知 ,复数 ( 为虚数单位)是纯虚数,则复数 的虚部是( )A、 B、 C、 D、3. 若 满足线性约束条件 ,则 的最小值是( )A、0 B、1 C、2 D、-14. 已知 , ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 函数 的图象大致是( )A、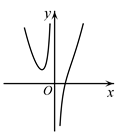 B、
B、 C、
C、 D、
D、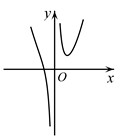 6. 已知实数 , 满足 ,则 的最小值是( )A、-2 B、 C、 D、-27. 已知不全相等的实数 , , 成等比数列,则一定不可能是等差数列的为( )A、 , , B、 , , C、 , , D、 , ,8. 甲、乙、丙、丁、戊5个人分到 三个班,要求每班至少一人,则甲不在A班的分法种数有( )A、160 B、112 C、100 D、869. 已知三棱锥 的所有棱长均为2, 为 的中点,空间中的动点 满足 , ,则动点 的轨迹长度为( )A、 B、 C、 D、10. 已知双曲线 的左、右焦点分别为 、 , 是双曲线 上的一点,且 满足 , ,则双曲线 的离心率为( )A、 B、 C、 D、
6. 已知实数 , 满足 ,则 的最小值是( )A、-2 B、 C、 D、-27. 已知不全相等的实数 , , 成等比数列,则一定不可能是等差数列的为( )A、 , , B、 , , C、 , , D、 , ,8. 甲、乙、丙、丁、戊5个人分到 三个班,要求每班至少一人,则甲不在A班的分法种数有( )A、160 B、112 C、100 D、869. 已知三棱锥 的所有棱长均为2, 为 的中点,空间中的动点 满足 , ,则动点 的轨迹长度为( )A、 B、 C、 D、10. 已知双曲线 的左、右焦点分别为 、 , 是双曲线 上的一点,且 满足 , ,则双曲线 的离心率为( )A、 B、 C、 D、二、填空题
-
11. 已知某三棱柱的三视图如图所示,那么该三棱柱的体积为 , 表面积为.
 12. 已知直线 与圆 ,若 ,直线 与圆相交于 , 两点,则 , 若直线 与圆相切,则实数 .13. 某同学在上学路要经过两个红绿灯十字路口,已知他在第一个十字路口遇到红灯的概率为 ,若他在第一个十字路口遇到红灯,则在第二个十字路口遇到红灯的概率为 ;若他在第一个十字路口遇到绿灯,则在第二个十字路口遇到红灯的概率为 .记他在上学路上遇到红灯的次数为 ,则 , 的数学期望为.14. 已知 ,则 , .15. 已知函数 , 的最小值为 ,则实数 所有取值组成的集合为.16. 设 , 为单位向量,则 的最大值是17. 已知 ,设函数 ,存在 满足 ,且 ,则 的取值范围是.
12. 已知直线 与圆 ,若 ,直线 与圆相交于 , 两点,则 , 若直线 与圆相切,则实数 .13. 某同学在上学路要经过两个红绿灯十字路口,已知他在第一个十字路口遇到红灯的概率为 ,若他在第一个十字路口遇到红灯,则在第二个十字路口遇到红灯的概率为 ;若他在第一个十字路口遇到绿灯,则在第二个十字路口遇到红灯的概率为 .记他在上学路上遇到红灯的次数为 ,则 , 的数学期望为.14. 已知 ,则 , .15. 已知函数 , 的最小值为 ,则实数 所有取值组成的集合为.16. 设 , 为单位向量,则 的最大值是17. 已知 ,设函数 ,存在 满足 ,且 ,则 的取值范围是.三、解答题
-
18. 设常数 ,已知 .
(Ⅰ)若 是奇函数,求 的值及 的单调递增区间;
(Ⅱ)设 , 中,内角 , , 的对边分别为 , , .若 ,且 的面积 ,求 周长的取值范围.
19. 如图,四边形 中,满足 , , , , ,将 沿 翻折至 ,使得 .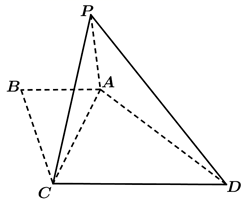
(Ⅰ)求证:平面 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值.
20. 已知数列 , 中, , , , , .(Ⅰ)证明 是等比数列,并求 的通项公式;
(Ⅱ)设 ,求数列 的前 项和 .
