陕西省西安市长安区2021届高三下学期理数二模试卷
试卷更新日期:2021-05-18 类型:高考模拟
一、单选题
-
1. 设集合 , ,若 ,则实数 的取值范围是( )A、 B、 C、 D、2. 若复数 满足: ( 为虚数单位),则 等于( )A、 B、 C、 D、3. 已知“x>2”是“ <1”的( )条件.A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要4. 设 , , ,则( )A、 B、 C、 D、5. 函数 y=lncosx() 的图象是( )A、
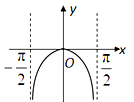 B、
B、 C、
C、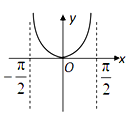 D、
D、 6. 设 是两条不同的直线, 是一个平面,则下列说法正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则7. 在 的展开式中, 的系数是14,则 的系数是( )A、28 B、56 C、112 D、2248. 等差数列 中, ,前 项和为 ,若 ,则 ( )A、1010 B、2020 C、1011 D、20219. 在 中, 是 的中点,已知 , , ,则 的面积为( )A、 B、 C、 D、10. 2019年10月,德国爆发出“芳香烃门”事件,即一家权威的检测机构在德国销售的奶粉中随机抽检了16款(德国4款,法国8款,荷兰4款),其中8款检测出芳香烃矿物油成分,此成分会严重危害婴幼儿的成长,有些奶粉已经远销至中国.A地区闻讯后,立即组织相关检测员对这8款品牌的奶粉进行抽检,已知该地区有6家婴幼儿用品商店在售这几种品牌的奶粉,甲、乙、丙3名检测员分别负责进行检测,每人至少抽检1家商店,且检测过的商店不重复检测,则甲检测员至少检测3家商店的概率为( )A、 B、 C、 D、11. 已知双曲线 : 的左、右焦点分别为 , ,过点 且斜率为 的直线与双曲线在第二象限的交点为A,若 ,则双曲线C的渐近线方程是( )A、 B、 C、 D、12. 已知四棱锥 的底面 是矩形,其中 , ,面 面 , ,且直线 与 所成角的余弦值为 ,则四棱锥 的外接球表面积为( )A、 B、 C、 D、
6. 设 是两条不同的直线, 是一个平面,则下列说法正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则7. 在 的展开式中, 的系数是14,则 的系数是( )A、28 B、56 C、112 D、2248. 等差数列 中, ,前 项和为 ,若 ,则 ( )A、1010 B、2020 C、1011 D、20219. 在 中, 是 的中点,已知 , , ,则 的面积为( )A、 B、 C、 D、10. 2019年10月,德国爆发出“芳香烃门”事件,即一家权威的检测机构在德国销售的奶粉中随机抽检了16款(德国4款,法国8款,荷兰4款),其中8款检测出芳香烃矿物油成分,此成分会严重危害婴幼儿的成长,有些奶粉已经远销至中国.A地区闻讯后,立即组织相关检测员对这8款品牌的奶粉进行抽检,已知该地区有6家婴幼儿用品商店在售这几种品牌的奶粉,甲、乙、丙3名检测员分别负责进行检测,每人至少抽检1家商店,且检测过的商店不重复检测,则甲检测员至少检测3家商店的概率为( )A、 B、 C、 D、11. 已知双曲线 : 的左、右焦点分别为 , ,过点 且斜率为 的直线与双曲线在第二象限的交点为A,若 ,则双曲线C的渐近线方程是( )A、 B、 C、 D、12. 已知四棱锥 的底面 是矩形,其中 , ,面 面 , ,且直线 与 所成角的余弦值为 ,则四棱锥 的外接球表面积为( )A、 B、 C、 D、二、填空题
-
13. 已知 , , , ,则 与 的夹角 的余弦值为 .14. 设 满足约束条件 ,则 的取值范围为 .15. 已知 是定义域为 的函数 的导函数,若对任意实数 都有 ,且有 ,则不等式 的解集为 .16. 任取一个正整数m , 若m是奇数,就将该数乘3再加上1;若m是偶数,就将该数除以2.反复进行上述两种运算,经过有限次步骤后,必进入循环圈1→4→2→1,这就是数学史上著名的“冰雹猜想”(又称“角谷猜想”等),若 ,则经过次步骤后变成1;若第5次步骤后变成1,则m的所有可能取值组成的集合为 .
三、解答题
-
17. 已知函数 经过点 ,且在区间 上单调.(1)、求函数 的解析式.(2)、设 ,求数列 的前60项和 .18. 已知等腰梯形 ,如图(1)所示, , ,沿 将△ 折起,使得平面 平面 ,如图(2)所示,连接 ,得三棱锥 .

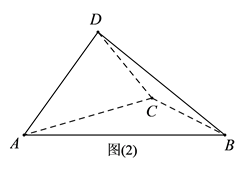 (1)、求证:图(2)中 平面 ;(2)、求图(2)中的二面角 的正弦值.19. 为了迎接十四运,提高智慧城市水平,西安公交公司近期推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如表下所示:
(1)、求证:图(2)中 平面 ;(2)、求图(2)中的二面角 的正弦值.19. 为了迎接十四运,提高智慧城市水平,西安公交公司近期推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如表下所示:x
1
2
3
4
5
6
7
y
6
11
21
34
66
101
196
根据以上数据,绘制了散点图.
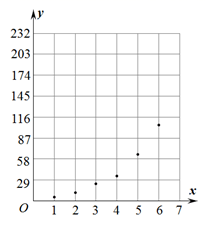 (1)、根据散点图判断,在推广期内, 与 ( 均为大于零的常数),哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);(2)、根据(1)的判断结果及表1中的数据,建立y与x的回归方程,并预测活动推出第8天使用扫码支付的人次;(3)、推广期结束后,车队对乘客的支付方式进行统计,结果如下表:
(1)、根据散点图判断,在推广期内, 与 ( 均为大于零的常数),哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);(2)、根据(1)的判断结果及表1中的数据,建立y与x的回归方程,并预测活动推出第8天使用扫码支付的人次;(3)、推广期结束后,车队对乘客的支付方式进行统计,结果如下表:支付方式
现金
乘车卡
扫码
比例
10%
60%
30%
西安公交六公司车队为缓解周边居民出行压力,以90万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为0.66万元.已知该线路公交车票价为2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有 的概率享受7折优惠,有 的概率享受8折优惠,有 的概率享受9折优惠.预计该车队每辆车每个月有2万人次乘车,根据所给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,请你估计这批车辆需要几年(结果取整数年)才能盈利?
参考数据:
62.14
1.54
2535
50.12
3.47
其中其中 , ,
参考公式:对于一组数据 , ,…, ,其回归直线 的斜率和截距的最小二乘估计公式分别为: , .
20. 已知点 , ,动点 满足直线 与 的斜率之积为 ,记动点 的轨迹为曲线 .(1)、求 的方程,并说明 是什么曲线.(2)、曲线 与 轴正半轴的交点为点 ,点 是曲线 上的一点(点 不在坐标轴上),若直线 与直线 交于点 ,直线 与直线 交于点 ,求证: 为等腰三角形.