湘教版备考2021年中考数学三轮复习专题4方程与不等式综合

试卷更新日期：2021-05-18 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 从﹣4，﹣3，1，3，4这五个数中，随机抽取一个数，记为m，若m使得关于x，y的二元一次方程组 ${\begin{matrix} 2 x + y = 2 \\ m x - 2 y = 3 \end{matrix}$ 有解，且使关于x的分式方程 $\frac{1 - m}{x - 1}$ ﹣1= $\frac{2}{1 - x}$ 有正数解，那么这五个数中所有满足条件的m的值之和是（）

A、1 B、2 C、﹣1 D、﹣2

查看试题解析
2. 若关于x的不等式组 ${\begin{matrix} \frac{5 x - 3}{6} \leq \frac{1}{2} + \frac{x}{3} \\ 5 x \geq a \end{matrix}$ 有且只有三个整数解，且关于x的分式方程 $\frac{x}{x - 2}$ ﹣ $\frac{a + 1}{2 - x}$ =﹣1有整数解，则满足条件的整数a的值为（）

A、15 B、3 C、﹣1 D、﹣15

查看试题解析
3. 若关于 $x$ 的一元一次不等式组 ${\begin{matrix} x - a > 0 \\ 1 - 2 x > x - 2 \end{matrix}$ 无解，则 $a$ 的取值范围是（）

A、 $a$ ≥1 B、 $a$ ＞1 C、 $a$ ≤ $- 1$ D、 $a$ ＜ $- 1$

查看试题解析
4. 已知关于x的不等式组 ${\begin{matrix} 2 a + 3 x > 0 \\ 3 a - 2 x \geq 0 \end{matrix}$ 恰有3个整数解，则a的取值范围是（）

A、 $\frac{2}{3} \leq a \leq \frac{3}{2}$ B、 $\frac{4}{3} \leq a \leq \frac{3}{2}$ C、 $\frac{4}{3} < a \leq \frac{3}{2}$ D、 $\frac{4}{3} \leq a < \frac{3}{2}$

查看试题解析
5. 若 $a$ ， $b$ ， $c$ 是 $Δ A B C$ 的三边长，且 $a^{2} + b^{2} + c^{2} - a b - a c - b c = 0$ ，则 $Δ A B C$ 的形状是（）

A、等腰三角形 B、等腰直角三角形 C、等边三角形 D、不能确定

查看试题解析
6. 已知关于x的一元二次方程(a－1)x²－2x+1=0有两个不相等的实数根,则a的取值范围是( ).

A、a<2 B、a>2 C、a<2且a≠1 D、a<－2

查看试题解析
7. 某种商品的进价为1200元，标价为1575元，后来由于该商品积压，商店准备打折出售，但要保持利润率不低于5%，则至多可打（　　　）

A、6折 B、7折 C、8折 D、9折

查看试题解析
8. 有一根长40mm的金属棒，欲将其截成x根7mm长的小段和y根9mm长的小段，剩余部分作废料处理，若使废料最少，则正整数x，y应分别为（）

A、x=1，y=3 B、x=3，y=2 C、x=4，y=1 D、x=2，y=3

查看试题解析
9. 一个教室有5盏灯，其中有40瓦和60瓦的两种，总的瓦数为260瓦，则40瓦和60瓦的灯泡个数分别是（）

A、1，4 B、2，3 C、3，2 D、 4，1

查看试题解析
10. 已知不等式组 $\{\begin{matrix} x > - 1 \\ x < a \end{matrix}$ 只有一个整数解，则a的取值范围一定只能为

A、a≤1 B、0≤a＜1 C、0＜a≤1 D、0＜a＜1

查看试题解析

二、填空题

11. 我国过年历史悠久，在传承发展中己形成了一些较为固定的习俗，有许多还相传至今，如买年货、扫尘、贴对联、吃年夜饭、守岁、拜岁、拜年、舞龙舞狮、拜神祭祖、祈福攘灾、游神、押舟、庙会、游锣鼓、游标旗、上灯酒、赏花灯等.某商店新进一批“福”字贴画和数对灯笼（灯笼一对为2件），共超过250件但不超过300件，灯笼的对数正好是“福”字贴画数量的 $\frac{1}{5}$ ，每张“福”字贴画进价是4元，每对灯笼的进价是50元（灯笼成对出售），商店将“福”字贴画以高出进价的 $\frac{3}{4}$ 售出，将灯笼每对按高出进价的40%售出，最后留下了35件物品未卖出，并把这批物品免费送给了自己的亲戚朋友，最后商店经过计算总利润率为20%，则最初购进灯笼对.

查看试题解析
12. 关于 $x, y$ 的方程组 ${\begin{cases} x - y = 1 + 3 m \\ x + 3 y = 1 + m \end{cases} \begin{array}{l} \end{array}$ 的解 $x$ 与 $y$ 满足条件 $x + y \leq 2$ ，则 $4 m + 3$ 的最大值是．

查看试题解析
13. 若不等式3x-m≤0的正整数解恰好是1、2、3，则m的取值范围是.

查看试题解析
14. 若不等式组 ${\begin{matrix} x > a + 1 \\ x - 3 < 0 \end{matrix}$ 有三个整数解，则 $a$ 的取值范围是.

查看试题解析
15. 已知关于x的一元二次方程x²+（2k+1）x+k²﹣2=0的两根为x₁和x₂ ，且（x₁﹣2）（x₁﹣x₂）=0，则k的值是．

查看试题解析
16. 如果关于x的不等式组 ${\begin{cases} x > a + 2 \\ x < 3 a - 2 \end{cases}$ 无解，则字母 $a$ 的取值范围是.

查看试题解析
17. 已知方程（a-2）x^|a|-1=1是一元一次方程，则a= ， x= ．

查看试题解析

三、解答题

18. 已知关于x、y的方程组 ${\begin{array}{l} a x + y = 5 ① \\ 4 x - b y = 7 ② \end{array}$ ，甲由于看错了方程①中的a ，得到方程组的解为 ${\begin{array}{l} x = 3 \\ y = 5 \end{array}$ ；乙由于看错了方程②中的b ，得到方程组的解为 ${\begin{array}{l} x = - 1 \\ y = 7 \end{array}$ ．求原方程组的正确解．

查看试题解析
19. 在实数范围内只有一个实数是关于x的方程 $\frac{k (x - 1)}{x} + \frac{2 k + 1}{x^{2} + x} = 1 + \frac{2 k}{x + 1}$ 的根，求实数k的所有可能值.

查看试题解析
20. 某校为了做好大课间活动，计划用400元购买10件体育用品，备选体育用品及单价如下表（单位：元）

备选体育用品

篮球

排球

羽毛球拍

单价（元）

50

40

25

(1)、若400元全部用来购买篮球和羽毛球拍共10件，问篮球和羽毛球拍各购买多少件？

(2)、若400元全部用来购买篮球、排球和羽毛球拍三种共10件，能实现吗？（若能实现直接写出一种答案即可，若不能请说明理由.）

查看试题解析
21. 已知关于x ， y的二元一次方程组 ${\begin{array}{l} 5 x + 3 y = n \\ 3 x - 2 y = 2 n + 1 \end{array}$ 的解适合方程x＋y＝6，求n的值．

查看试题解析
22. 百脑汇商场中路路通商店有甲、乙两种手机内存卡，买2个甲内存卡和1个乙内存卡用了90元，买3个甲内存卡和2个乙内存卡用了160元．

(1)、求甲、乙两种内存卡每个各多少元？

(2)、如果小亮准备购买甲．乙两种手机内存卡共10个，总费用不超过350元，且不低于300元，问有几种购买方案，哪种方案费用最低？

(3)、某天，路路通售货员不小心把当天上午卖的甲、乙种手机内存卡的销售量统计单丢失了，但老板记得每件甲内存卡每个赚10元，乙内存卡每个赚15元，一上午售出的内存卡共赚了100元，请你帮助老板算算有几种销售方案？并直接写出销售方案．

查看试题解析
23. 如图，A和B两个小机器人，自甲处同时出发相背而行，绕直径为整数米的圆周上运动，15分钟内相遇7次，如果A的速度每分钟增加6米，则A和B在15分钟内相遇9次，问圆周直径至多是多少米？至少是多少米？（取π=3.14）

查看试题解析

四、综合题

24. 有一段6000米的道路由甲乙两个工程队负责完成．已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍，且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天．

(1)、求甲、乙两工程队每天各完成多少米？

(2)、如果甲工程队每天需工程费7000元，乙工程队每天需工程费5000元，若甲队先单独工作若干天，再由甲乙两工程队合作完成剩余的任务，支付工程队总费用不超过79000元，则两工程队最多可以合作施工多少天？

查看试题解析
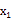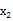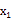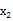25. 已知方程 +px+q＝0的两个根是，，那么 + ＝－p， $x_{1}$ $x_{2}$ ＝q，反过来，如果 $x_{1}$ + $x_{2}$ ＝－p， $x_{1}$ $x_{2}$ ＝q，那么以 $x_{1}$ ， $x_{2}$ 为两根的一元二次方程是 $x^{2}$ +px+q＝0．请根据以上结论，解决下列问题：

(1)、已知关于x的方程 $x^{2}$ +mx+n＝0(n≠0)，求出—个一元二次方程，使它的两根分别是已知方程两根的倒数．

(2)、已知a、b满足 $a^{2}$ －15a－5＝0， $b^{2}$ －15b－5＝0，求 $\frac{a}{b} + \frac{b}{a}$ 的值．

(3)、已知a、b、c均为实数，且a+b+c＝0，abc＝16，求正数c的最小值

查看试题解析
26. 已知关于 $x$ 的方程 $x^{2} + (2 k - 1) x + k^{2} - 1 = 0$ 有两个实数根 $x_{1}$ 、 $x_{2}$ ．

(1)、求实数k的取值范围；

(2)、若 $x_{1}$ 、 $x_{2}$ 满足 $x_{1}^{2} + x_{2}^{2} = 16 + x_{1} \cdot x_{2}$ ，求实数 $k$ 的值．

查看试题解析
27. 去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．

(1)、求饮用水和蔬菜各有多少件？

(2)、现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来；

(3)、在（2）的条件下，如果甲种货车每辆需付运费400元，乙种货车每辆需付运费360元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？

查看试题解析
28. 已知关于x的一元二次方程x²+（2m+1）x+m²﹣4=0

(1)、当m为何值时，方程有两个不相等的实数根？

(2)、若边长为5的菱形的两条对角线的长分别为方程两根的2倍，求m的值．

查看试题解析
29. 已知关于x的一元二次方程 2x²+4x+m-1 =0有两个非零实数根．

(1)、求m的取值范围；

(2)、两个非零实数根能否同为正数或同为负数？若能，请求出相应的m的取值范围，若不能，请说明理由．

查看试题解析
30. 已知关于x的方程x²-（2k-3）x+k²+1=0．问：

(1)、当k为何值时，此方程有实数根；

(2)、若此方程的两实数根x₁、x₂ ，满足|x₁|+|x₂|=3，求k的值．

查看试题解析

备选体育用品	篮球	排球	羽毛球拍
单价（元）	50	40	25