陕西省备考2021年中考数学二次函数真题专练

试卷更新日期：2021-05-18 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，将抛物线y＝x²﹣（m﹣1）x+m（m＞1）沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在同一平面直角坐标系中，若抛物线 $y = x^{2} + (2 m - 1) x + 2 m - 4$ 与 $y = x^{2} - (3 m + n) x + n$ 关于y轴对称，则符合条件的m，n的值为（）

A、m= $\frac{5}{7}$ ,n= $- \frac{18}{7}$ B、m=5，n= -6 C、m= -1，n=6 D、m=1，n= -2

查看试题解析
3. 对于抛物线y＝ax²＋(2a－1)x＋a－3，当x＝1时，y＞0，则这条抛物线的顶点一定在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 已知抛物线y=x²﹣2mx﹣4（m＞0）的顶点M关于坐标原点O的对称点为M′，若点M′在这条抛物线上，则点M的坐标为（）

A、（1，﹣5） B、（3，﹣13） C、（2，﹣8） D、（4，﹣20）

查看试题解析
5.
如图，观察二次函数y=ax²+bx+c的图象，下列结论：
①a+b+c＞0， ②2a+b＞0， ③b²﹣4ac＞0， ④ac＞0．其中正确的是（　　）

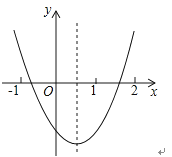A、①② B、①④ C、②③ D、③④

查看试题解析
6.
二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列结论：①2a+b＞0；②abc＜0；③b²﹣4ac＞0；④a+b+c＜0；⑤4a﹣2b+c＜0，其中正确的个数是（　　）

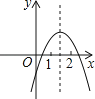A、2 B、3 C、4 D、5

查看试题解析

二、综合题

7. 已知抛物线L：y＝x²＋x－6与x轴相交于A、B两点（点A在点B的左侧），并与y轴相交于点C．

(1)、求A、B、C三点的坐标，并求出△ABC的面积；

(2)、将抛物线向左或向右平移，得到抛物线L´，且L´与x轴相交于A´、B´两点（点A´在点B´的左侧），并与y轴交于点C´，要使△A´B´C´和△ABC的面积相等，求所有满足条件的抛物线的函数表达式．

查看试题解析
8. 在同一直角坐标系中，抛物线C₁：y=ax²﹣2x﹣3与抛物线C₂：y=x²+mx+n关于y轴对称，C₂与x轴交于A，B两点，其中点A在点B的左侧．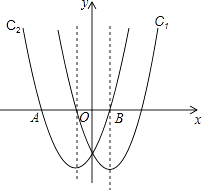

(1)、求抛物线C₁ ， C₂的函数表达式；

(2)、求A，B两点的坐标；

(3)、在抛物线C₁上是否存在一点P，在抛物线C₂上是否存在一点Q，使得以AB为边，且以A，B，P，Q四点为顶点的四边形是平行四边形？若存在，求出P、Q两点的坐标；若不存在，请说明理由．

查看试题解析
9. 在平面直角坐标系中，抛物线y=x²+5x+4的顶点为M，与x轴交于A，B两点，与y轴交于C点．

(1)、求点A，B，C的坐标

(2)、求抛物线y=x²+5x+4关于坐标原点O对称的抛物线的函数表达式

(3)、设（2）中所求抛物线的顶点为M′，与x轴交于A′，B′两点，与y轴交于C′点，在以A，B，C，M，A′，B′，C′，M′这八个点中的四个点为顶点的平行四边形中，求其中一个不是菱形的平行四边形的面积．

查看试题解析
10.
如图，一小球从斜坡O点处抛出，球的抛出路线可以用二次函数 $y = - x^{2} + 4 x$ 刻画，斜坡可以用一次函数y= $\frac{1}{2}$ x刻画．

(1)、请用配方法求二次函数图象的最高点P的坐标；

(2)、小球的落点是A，求点A的坐标；

(3)、连接抛物线的最高点P与点O、A得△POA，求△POA的面积

(4)、在OA上方的抛物线上存在一点M（M与P不重合），△MOA的面积等于△POA的面积．请直接写出点M的坐标

查看试题解析